7 Times What Equals 42
keralas
Sep 14, 2025 · 6 min read
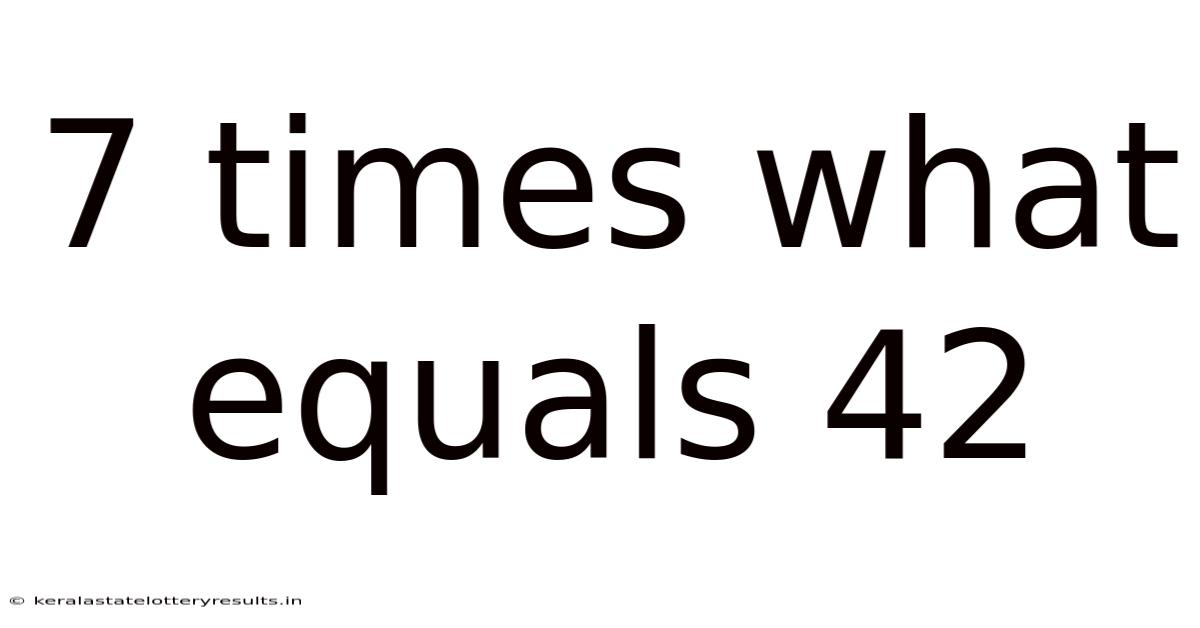
Table of Contents
7 Times What Equals 42? Unlocking the Power of Multiplication and Problem-Solving
The seemingly simple question, "7 times what equals 42?" acts as a gateway to understanding fundamental mathematical concepts, problem-solving strategies, and even the deeper meaning behind numerical relationships. This article will delve into this seemingly basic equation, exploring its solution, its relevance in various contexts, and the broader implications it holds for mathematical learning and beyond. We'll cover the core mathematical principle, explore different approaches to solving the problem, and touch upon its application in real-world scenarios. This will be a comprehensive guide suitable for anyone from elementary school students to those looking for a refresher on basic arithmetic.
Understanding the Fundamentals: Multiplication and Division
Before diving into the solution, let's establish the groundwork. The question "7 times what equals 42" is a multiplication problem expressed in a slightly different format. Multiplication is essentially repeated addition. For instance, 7 times 3 (written as 7 x 3 or 7 * 3) means adding 7 three times: 7 + 7 + 7 = 21. Conversely, division is the opposite of multiplication; it's the process of splitting a number into equal parts. To solve "7 times what equals 42," we're essentially looking for the number that, when multiplied by 7, results in 42.
Solving the Equation: Simple Methods
The most straightforward way to solve "7 times what equals 42" is through division. We know that multiplication and division are inverse operations, meaning they undo each other. Therefore, to find the missing number, we divide 42 by 7:
42 ÷ 7 = 6
Therefore, the answer is 6. Seven times six equals forty-two (7 x 6 = 42). This is a simple yet fundamental arithmetic operation that forms the basis for more complex mathematical concepts.
Visualizing the Problem: A Concrete Approach
For younger learners or those who prefer a more visual approach, using concrete objects can help solidify the understanding. Imagine having 42 blocks. If you want to divide these blocks into 7 equal groups, how many blocks will be in each group? By physically separating the blocks into 7 groups, you'll discover that each group contains 6 blocks, reinforcing the concept that 7 x 6 = 42.
Exploring Different Methods: Algebraic Approach
As we progress in mathematics, we encounter more sophisticated methods. The problem "7 times what equals 42" can be represented algebraically. We can use a variable, such as 'x', to represent the unknown number:
7x = 42
To solve for 'x', we perform the same division operation:
x = 42 ÷ 7 x = 6
This algebraic representation helps establish a foundation for solving more complex equations in the future. It introduces the concept of variables and the process of isolating the unknown variable to find its value.
Real-World Applications: Beyond the Classroom
The concept of "7 times what equals 42" isn't confined to theoretical mathematical problems. It has practical applications in everyday life:
- Shopping: If you need 7 packs of pencils, and each pack costs $6, the total cost will be 7 x $6 = $42.
- Baking: If a recipe calls for 7 tablespoons of flour per batch, and you have 42 tablespoons of flour, you can make 42 ÷ 7 = 6 batches.
- Equal Sharing: If you have 42 candies and you want to divide them equally among 7 friends, each friend will receive 6 candies.
- Distance Calculations: If you travel at a constant speed of 7 km/hour and cover a distance of 42 km, the travel time will be 42 km ÷ 7 km/hour = 6 hours.
These examples demonstrate how the seemingly simple equation has practical implications across various scenarios, illustrating its importance in everyday life.
The Significance of Problem Solving: Developing Critical Thinking
Solving the problem "7 times what equals 42" is more than just finding the answer; it's about developing crucial problem-solving skills. It encourages:
- Critical thinking: Analyzing the problem and identifying the appropriate mathematical operation to use.
- Logical reasoning: Understanding the relationship between multiplication and division and applying this understanding to find the solution.
- Numerical fluency: Developing comfort and proficiency with basic arithmetic operations.
- Persistence: Not giving up when faced with a mathematical challenge.
These skills are invaluable not only in mathematics but also in other academic disciplines and real-world situations.
Beyond the Basic: Expanding on the Concept
Once the basic concept is grasped, we can expand upon it by introducing related concepts:
- Factors and Multiples: The numbers 7 and 6 are factors of 42, meaning they divide 42 evenly. 42 is a multiple of both 7 and 6.
- Prime Factorization: We can break down 42 into its prime factors: 2 x 3 x 7. This shows the fundamental building blocks of the number.
- Order of Operations (PEMDAS/BODMAS): Understanding the order in which to perform mathematical operations becomes crucial when solving more complex problems.
These concepts build upon the foundation established by solving simple equations like "7 times what equals 42," showcasing the interconnectedness of mathematical ideas.
Addressing Potential Challenges: Common Mistakes and Solutions
While seemingly simple, students might encounter some difficulties:
- Confusion between multiplication and division: Clearly understanding the inverse relationship between these operations is essential. Using visual aids or concrete examples can help.
- Difficulty with times tables: Regular practice with multiplication tables can improve fluency and speed in solving problems.
- Procedural errors: Carefully checking calculations can minimize errors.
Frequently Asked Questions (FAQ)
-
Q: What is the best way to learn multiplication facts?
- A: Consistent practice through flash cards, games, and repetition is key. Try to connect multiplication facts to visual representations.
-
Q: How can I help my child understand this concept?
- A: Use real-world examples, visual aids, and hands-on activities to make learning engaging and memorable.
-
Q: Are there other ways to solve this problem besides division?
- A: You could use repeated subtraction (subtracting 7 repeatedly from 42 until you reach zero and counting the number of subtractions). However, division is the most efficient method.
-
Q: What if the number wasn't 42, but a different multiple of 7?
- A: The process remains the same; you would divide the given number by 7 to find the unknown factor.
Conclusion: The Enduring Power of a Simple Equation
The seemingly simple equation "7 times what equals 42?" serves as a powerful illustration of fundamental mathematical concepts and problem-solving skills. From the basic operation of division to its broader implications in algebraic representation and real-world applications, this equation provides a valuable stepping stone for developing a deeper understanding of mathematics. The ability to solve such problems not only demonstrates numerical fluency but also cultivates critical thinking, logical reasoning, and problem-solving skills—essential attributes applicable far beyond the realm of mathematics. By understanding the solution and exploring the various methods and contexts surrounding this equation, we uncover the enduring power of a seemingly simple question.
Latest Posts
Latest Posts
-
Gcf Of 21 And 24
Sep 14, 2025
-
Gcf Of 30 And 12
Sep 14, 2025
-
12 Is 60 Of What
Sep 14, 2025
-
9 20 To A Decimal
Sep 14, 2025
-
Whats 0 375 As A Fraction
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 7 Times What Equals 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.