Gcf Of 30 And 12
keralas
Sep 14, 2025 · 6 min read
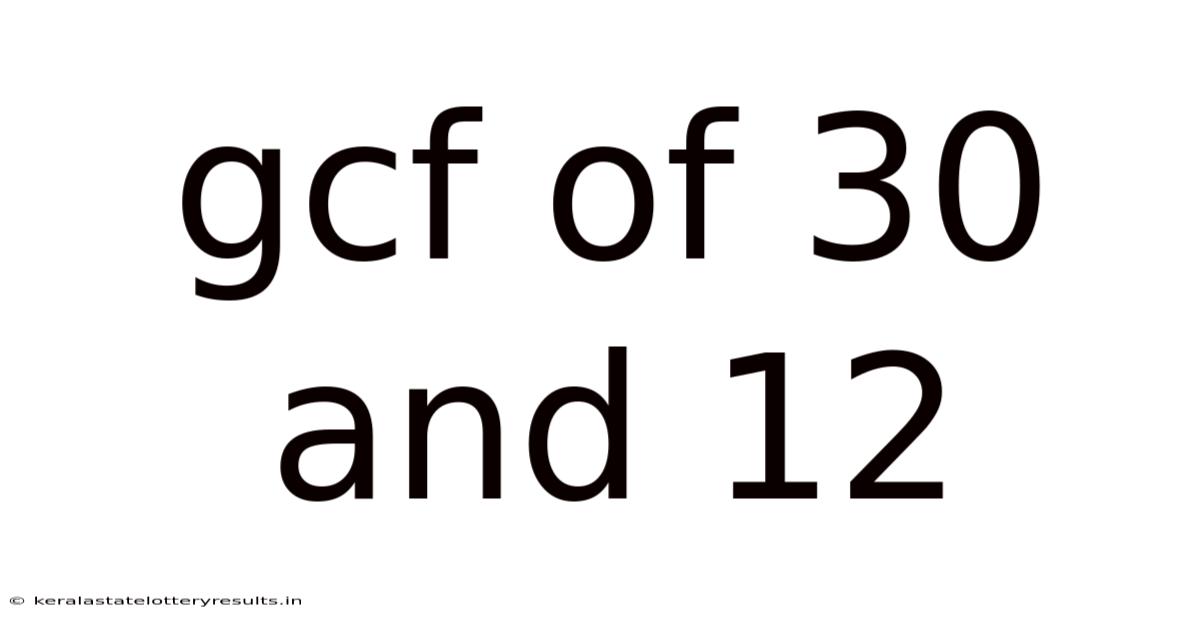
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 30 and 12: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving algebraic equations. This comprehensive guide will explore the GCF of 30 and 12, demonstrating various methods to calculate it and delving into the underlying mathematical principles. Understanding this seemingly simple concept unlocks a deeper appreciation for number theory and its practical uses.
Understanding Greatest Common Factor (GCF)
Before diving into the specifics of finding the GCF of 30 and 12, let's establish a solid understanding of the concept itself. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly. For example, the GCF of 8 and 12 is 4 because 4 is the largest number that divides both 8 and 12 without leaving a remainder.
Method 1: Prime Factorization
The prime factorization method is a robust and reliable approach for finding the GCF of any two numbers. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Step 1: Prime Factorization of 30
30 can be expressed as a product of its prime factors: 2 x 3 x 5
Step 2: Prime Factorization of 12
12 can be expressed as a product of its prime factors: 2 x 2 x 3 (or 2² x 3)
Step 3: Identifying Common Factors
Now, we compare the prime factorizations of 30 and 12:
30 = 2 x 3 x 5 12 = 2 x 2 x 3
The common factors are 2 and 3.
Step 4: Calculating the GCF
To find the GCF, we multiply the common prime factors together:
GCF(30, 12) = 2 x 3 = 6
Therefore, the greatest common factor of 30 and 12 is 6. This means that 6 is the largest number that divides both 30 and 12 without leaving a remainder.
Method 2: Listing Factors
This method involves listing all the factors of each number and then identifying the largest factor common to both.
Step 1: Factors of 30
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
Step 2: Factors of 12
The factors of 12 are: 1, 2, 3, 4, 6, 12
Step 3: Identifying Common Factors
Comparing the lists, we find the common factors: 1, 2, 3, and 6.
Step 4: Determining the GCF
The largest common factor is 6. Therefore, the GCF(30, 12) = 6.
This method is straightforward for smaller numbers but can become cumbersome for larger numbers with many factors.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Step 1: Repeated Subtraction (or Division with Remainder)
Let's start with 30 and 12.
- 30 - 12 = 18
- 18 - 12 = 6
- 12 - 6 = 6
Since we've reached two equal numbers (6 and 6), the GCF is 6.
A more efficient way to apply the Euclidean algorithm is through division with remainder.
- Divide 30 by 12: 30 = 12 x 2 + 6 (The remainder is 6)
- Divide 12 by the remainder 6: 12 = 6 x 2 + 0 (The remainder is 0)
When the remainder is 0, the previous divisor (6) is the GCF.
Therefore, GCF(30, 12) = 6. This method is significantly more efficient than repeated subtraction, especially with larger numbers.
Mathematical Explanation and Properties of GCF
The GCF is deeply rooted in the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers. The prime factorization method leverages this theorem to find the GCF. The common prime factors, raised to the lowest power they appear in either factorization, constitute the GCF.
Several important properties of the GCF are:
- Commutative Property: GCF(a, b) = GCF(b, a). The order of the numbers doesn't affect the result.
- Associative Property: GCF(a, GCF(b, c)) = GCF(GCF(a, b), c). This allows for extending the GCF calculation to more than two numbers.
- Distributive Property (with LCM): GCF(a, b) x LCM(a, b) = a x b, where LCM represents the least common multiple. This relationship provides a powerful link between GCF and LCM.
- GCF of 1: If GCF(a, b) = 1, then a and b are said to be relatively prime or coprime. This means they share no common factors other than 1.
Applications of GCF
Understanding and calculating the GCF has numerous practical applications in mathematics and beyond:
- Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 30/12 can be simplified by dividing both the numerator and denominator by their GCF (6), resulting in the simplified fraction 5/2.
- Solving Equations: GCF plays a role in solving Diophantine equations, which involve finding integer solutions.
- Geometry and Measurement: GCF is used in problems involving finding the dimensions of squares or rectangles with specific constraints.
- Modular Arithmetic: GCF is essential in understanding modular arithmetic, which has applications in cryptography and computer science.
- Data Analysis: GCF can be helpful in simplifying ratios and proportions in data analysis.
Frequently Asked Questions (FAQ)
Q: What if the GCF is 1?
A: If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. They share no common factors other than 1.
Q: Can the GCF be negative?
A: While the process of finding the GCF might involve negative numbers during intermediate steps (like in repeated subtraction), the final result, the GCF itself, is always a positive integer.
Q: Which method is best for finding the GCF?
A: For smaller numbers, listing factors or prime factorization can be efficient. However, the Euclidean algorithm is the most efficient method for larger numbers, particularly those with many factors.
Q: How can I check my answer?
A: You can verify your GCF by ensuring that it divides both numbers evenly (without leaving a remainder) and that no larger number satisfies this condition.
Conclusion
Finding the greatest common factor of 30 and 12, which is 6, provides a practical illustration of a fundamental concept in number theory. We've explored three distinct methods – prime factorization, listing factors, and the Euclidean algorithm – each offering a unique approach to solving this problem. Understanding the GCF is not merely an exercise in arithmetic; it's a gateway to appreciating the deeper structures and relationships within the number system. The applications of GCF extend far beyond basic calculations, impacting various fields of mathematics and beyond. Mastering this concept provides a solid foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
Convert 64 Inches To Feet
Sep 14, 2025
-
Lcm Of 21 And 9
Sep 14, 2025
-
40 Minutes From Now Google
Sep 14, 2025
-
Can You Square Root 0
Sep 14, 2025
-
Gram Of Meth On Scale
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 30 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.