12 Is 60 Of What
keralas
Sep 14, 2025 · 5 min read
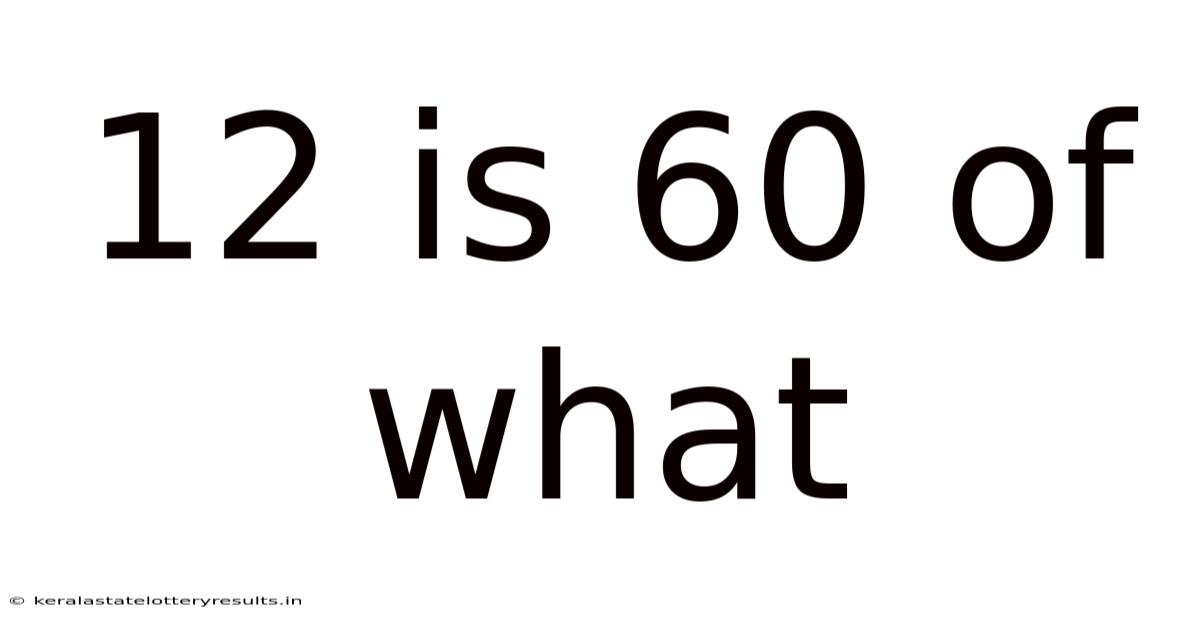
Table of Contents
12 is 60% of What: A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts in a store to analyzing financial data. This article will delve into the question, "12 is 60% of what?", providing a step-by-step solution, exploring the underlying mathematical principles, and offering practical applications to solidify your understanding of percentage calculations. We will also explore different methods for solving similar problems and address frequently asked questions. This comprehensive guide will leave you confident in tackling percentage problems of all kinds.
Understanding the Problem: 12 is 60% of What?
The question "12 is 60% of what?" essentially asks us to find the original value (or whole) from which 60% represents 12 units. This is a common type of percentage problem, and mastering its solution is crucial for various real-world applications, including calculating sales tax, determining original prices after discounts, and interpreting statistical data.
Step-by-Step Solution: Finding the Original Value
There are several ways to solve this problem. Let's explore the most common and straightforward approaches:
Method 1: Using the Equation Method
This method involves setting up a simple algebraic equation to represent the problem:
- Let 'x' represent the original value we are trying to find.
- 60% of x is equal to 12. We can express 60% as a decimal (0.6) or a fraction (60/100).
Therefore, our equation is:
0.6x = 12
To solve for 'x', we divide both sides of the equation by 0.6:
x = 12 / 0.6
x = 20
Therefore, 12 is 60% of 20.
Method 2: Using Proportions
This method involves setting up a proportion, which is a statement that two ratios are equal. We can represent the problem as:
12/x = 60/100
Here, 12 represents the part, x represents the whole, 60 represents the percentage, and 100 represents the total percentage (100%).
To solve for 'x', we cross-multiply:
12 * 100 = 60 * x
1200 = 60x
Divide both sides by 60:
x = 1200 / 60
x = 20
Again, we find that 12 is 60% of 20.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our case:
- Part = 12
- Percentage = 60
- Whole = x (what we need to find)
Substituting these values into the formula:
(12 / x) * 100 = 60
Now, we solve for x:
1200 / x = 60
x = 1200 / 60
x = 20
This method confirms that 12 is 60% of 20.
Practical Applications and Real-World Examples
Understanding how to solve percentage problems like "12 is 60% of what?" has numerous real-world applications:
-
Sales and Discounts: Imagine a store offering a 40% discount on an item, resulting in a $12 savings. Using the same principles, you can determine the original price of the item.
-
Financial Analysis: In finance, understanding percentages is essential for calculating returns on investment, interest rates, and analyzing financial statements.
-
Statistical Interpretation: Many statistical measures, such as percentages, proportions, and rates, rely on the ability to calculate and interpret percentages accurately.
Expanding Your Understanding: Variations and Further Challenges
While this article focuses on the specific problem "12 is 60% of what?", the underlying principles can be applied to a wide range of percentage problems. Let's explore some variations:
-
Finding the percentage: If you know the part and the whole, you can easily calculate the percentage. For example, what percentage is 8 of 20? The answer is (8/20) * 100 = 40%.
-
Finding the part: If you know the percentage and the whole, you can calculate the part. For instance, what is 30% of 50? The answer is 0.3 * 50 = 15.
The Importance of Accuracy in Percentage Calculations
Accuracy is crucial when working with percentages, especially in situations with financial implications. Even small errors in percentage calculations can have significant consequences. Double-checking your work and using multiple methods to verify your answers are always good practices.
Frequently Asked Questions (FAQ)
Q1: Can I solve this problem using a calculator?
A1: Absolutely! Most calculators have percentage functions that can simplify these calculations. You can directly input the values into the calculator, ensuring to correctly represent the percentage as a decimal.
Q2: What if the percentage is not a whole number?
A2: The same methods apply, even if the percentage is a decimal or a fraction. For example, if you are asked to find the number whose 12.5% is 5, the equation would be 0.125x = 5.
Q3: Are there other ways to visualize this problem?
A3: Yes! You can visualize this using a bar model or a pie chart, which are especially helpful in illustrating the relationship between the part and the whole.
Q4: Why is understanding percentages important?
A4: Percentages are a fundamental tool for understanding proportions and ratios, crucial for various applications in mathematics, science, business, and everyday life.
Conclusion
Solving percentage problems like "12 is 60% of what?" requires a clear understanding of the fundamental principles involved. This article has explored multiple methods for solving such problems, emphasizing accuracy and providing practical applications. By mastering percentage calculations, you significantly enhance your analytical skills, equipping yourself to tackle a wider range of challenges in various fields. Remember to practice regularly and explore different approaches to reinforce your understanding and improve your problem-solving abilities. The more you practice, the more confident and efficient you will become in tackling percentage problems.
Latest Posts
Latest Posts
-
Convert 64 Inches To Feet
Sep 14, 2025
-
Lcm Of 21 And 9
Sep 14, 2025
-
40 Minutes From Now Google
Sep 14, 2025
-
Can You Square Root 0
Sep 14, 2025
-
Gram Of Meth On Scale
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 12 Is 60 Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.