What's 0.375 As A Fraction
keralas
Sep 14, 2025 · 5 min read
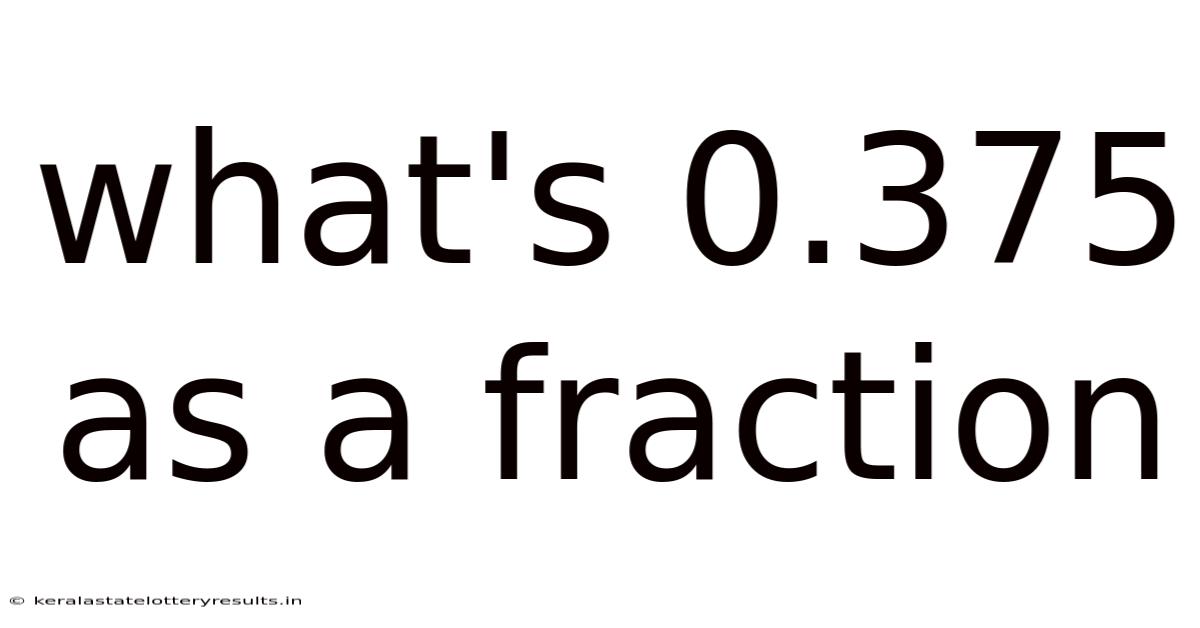
Table of Contents
What's 0.375 as a Fraction? A Comprehensive Guide
Understanding decimal-to-fraction conversion is a fundamental skill in mathematics. This comprehensive guide will walk you through the process of converting the decimal 0.375 into its fractional equivalent, explaining the method in detail and providing additional context to build your understanding of fractions and decimals. We'll explore different approaches, address common misconceptions, and delve into the underlying principles. By the end, you'll not only know the answer but also understand why the answer is what it is.
Understanding Decimals and Fractions
Before we dive into the conversion, let's briefly refresh our understanding of decimals and fractions.
-
Decimals: Decimals represent numbers that are not whole numbers. They use a base-ten system, with digits to the right of the decimal point representing fractions of powers of ten (tenths, hundredths, thousandths, and so on). For example, 0.375 represents 3 tenths, 7 hundredths, and 5 thousandths.
-
Fractions: Fractions represent parts of a whole. They are expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Converting 0.375 to a Fraction: The Step-by-Step Method
There are several ways to convert 0.375 to a fraction. Here's the most straightforward method:
1. Write the decimal as a fraction with a denominator of 1:
This is our starting point. We can write 0.375 as 0.375/1. This doesn't change the value, just its representation.
2. Multiply the numerator and denominator by a power of 10 to remove the decimal point:
Since there are three digits after the decimal point, we need to multiply both the numerator and denominator by 1000 (10<sup>3</sup>). This shifts the decimal point three places to the right.
(0.375 * 1000) / (1 * 1000) = 375/1000
3. Simplify the fraction:
Now we need to simplify the fraction 375/1000 to its lowest terms. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
To find the GCD of 375 and 1000, we can use the Euclidean algorithm or prime factorization. Let's use prime factorization:
- 375 = 3 × 5<sup>3</sup>
- 1000 = 2<sup>3</sup> × 5<sup>3</sup>
The GCD is 5<sup>3</sup> = 125.
Now, divide both the numerator and the denominator by 125:
375 ÷ 125 = 3 1000 ÷ 125 = 8
Therefore, the simplified fraction is 3/8.
Alternative Methods for Conversion
While the previous method is the most common, let's explore a couple of alternative approaches:
Method 2: Using Place Value Understanding
We know that 0.375 means 3/10 + 7/100 + 5/1000. To add these fractions, we need a common denominator, which is 1000. So we rewrite the fractions:
3/10 = 300/1000 7/100 = 70/1000 5/1000 = 5/1000
Adding them together: 300/1000 + 70/1000 + 5/1000 = 375/1000
This fraction then simplifies to 3/8, as shown in the previous method.
Method 3: Recognizing Common Decimal Equivalents
With practice, you might start recognizing common decimal-fraction equivalents. For example, you might know that 1/8 = 0.125. Since 0.375 is three times 0.125, it follows that 0.375 = 3/8.
The Importance of Simplification
Simplifying fractions is crucial because it presents the fraction in its most concise and easily understandable form. While 375/1000 is technically correct, 3/8 is much simpler and easier to work with in further calculations or comparisons. Always aim to simplify your fractions to their lowest terms.
Understanding the Concept of Equivalence
It's important to understand that while 0.375, 375/1000, and 3/8 represent the same value, they are different representations of that value. The fraction 3/8 is the simplified form, representing the most efficient way to express the ratio.
Frequently Asked Questions (FAQ)
Q: Can I convert any decimal to a fraction using this method?
A: Yes, this method works for any terminating decimal (a decimal that ends). For repeating decimals (decimals with digits that repeat infinitely), a slightly different method is required, involving setting up an equation and solving for the variable.
Q: What if I get a fraction that cannot be simplified?
A: If the greatest common divisor of the numerator and denominator is 1, the fraction is already in its simplest form. For example, 7/11 cannot be simplified further.
Q: Are there any online tools to help with decimal-to-fraction conversion?
A: Yes, many online calculators and converters can perform this task quickly and accurately. However, understanding the underlying process is crucial for building your mathematical skills.
Q: Why is understanding decimal-to-fraction conversion important?
A: It's fundamental to a strong grasp of mathematical concepts, particularly in areas like algebra, calculus, and various scientific applications. It also strengthens your number sense and problem-solving abilities.
Conclusion
Converting 0.375 to a fraction involves a clear and methodical process. Understanding the steps, from writing the decimal as a fraction over 1 to simplifying the resulting fraction to its lowest terms (3/8), is key. This guide provided multiple methods, emphasizing the importance of simplification and highlighting the underlying mathematical principles. Mastering this conversion not only gives you the answer but equips you with valuable problem-solving skills applicable to broader mathematical contexts. Remember, practice is key to solidifying your understanding and making this process second nature. Keep practicing, and you'll become confident in tackling decimal-to-fraction conversions with ease.
Latest Posts
Latest Posts
-
Lcm Of 21 And 9
Sep 14, 2025
-
40 Minutes From Now Google
Sep 14, 2025
-
Can You Square Root 0
Sep 14, 2025
-
Gram Of Meth On Scale
Sep 14, 2025
-
How Much Is 71 Kg
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What's 0.375 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.