1 1/2 In Decimal Form
keralas
Sep 16, 2025 · 5 min read
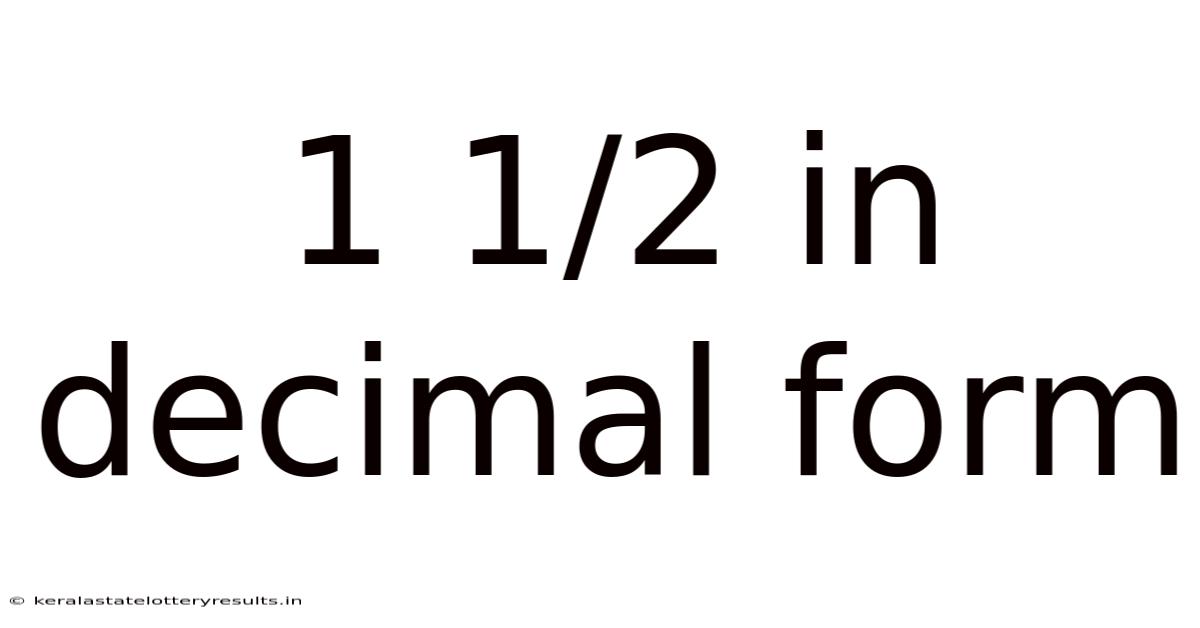
Table of Contents
1 1/2 in Decimal Form: A Comprehensive Guide
Understanding fractions and their decimal equivalents is a fundamental skill in mathematics. This comprehensive guide will delve into converting the mixed number 1 1/2 into its decimal form, explaining the process in detail and exploring related concepts. We'll cover multiple methods, address common questions, and provide examples to solidify your understanding. By the end, you'll not only know the decimal equivalent of 1 1/2 but also possess a deeper understanding of fraction-to-decimal conversions.
Understanding Fractions and Decimals
Before we tackle the conversion, let's briefly review the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 1/2, 1 is the numerator and 2 is the denominator. This means one out of two equal parts.
A decimal is another way to represent a part of a whole. It uses a base-ten system, with digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on. For example, 0.5 represents five-tenths, or half.
Mixed numbers, like 1 1/2, combine a whole number and a fraction. They represent a quantity greater than one.
Method 1: Converting the Fraction to a Decimal
The simplest method to convert 1 1/2 to a decimal involves converting the fractional part (1/2) to a decimal and then adding it to the whole number (1).
-
Step 1: Divide the numerator by the denominator. In our case, we divide 1 (numerator) by 2 (denominator): 1 ÷ 2 = 0.5
-
Step 2: Add the whole number. Now, we add the result from Step 1 to the whole number part of the mixed fraction: 1 + 0.5 = 1.5
Therefore, 1 1/2 in decimal form is 1.5.
Method 2: Converting the Mixed Number to an Improper Fraction
This method involves first converting the mixed number into an improper fraction, and then dividing the numerator by the denominator.
-
Step 1: Convert to an improper fraction. To do this, we multiply the whole number by the denominator and add the numerator. This becomes the new numerator, while the denominator remains the same.
1 1/2 = (1 * 2 + 1) / 2 = 3/2
-
Step 2: Divide the numerator by the denominator. Now, we divide the numerator (3) by the denominator (2): 3 ÷ 2 = 1.5
Again, we arrive at the decimal equivalent of 1.5.
Method 3: Using Equivalent Fractions
This method is less direct but demonstrates a deeper understanding of fractions. We can find an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000). This makes the conversion to decimal straightforward.
-
Step 1: Find an equivalent fraction with a denominator of 10. To make the denominator 10, we multiply both the numerator and the denominator of 1/2 by 5: (1 * 5) / (2 * 5) = 5/10
-
Step 2: Convert the fraction to a decimal. Since the denominator is 10, the fraction 5/10 is equivalent to 0.5.
-
Step 3: Add the whole number. Add the whole number 1: 1 + 0.5 = 1.5
This reinforces that 1 1/2 is equal to 1.5 in decimal form.
Illustrative Examples: Expanding the Concept
Let's expand our understanding by looking at similar conversions:
-
2 1/2: Following the same methods, we find that 2 1/2 = 2.5.
-
3 1/4: This example involves a fraction with a denominator other than 2 or a power of 10. Using the division method (Method 1): 1 ÷ 4 = 0.25, then 3 + 0.25 = 3.25.
-
1 3/4: Converting to an improper fraction (Method 2): (1 * 4 + 3) / 4 = 7/4. Then, 7 ÷ 4 = 1.75.
These examples showcase the adaptability of these methods for various mixed numbers.
The Importance of Understanding Decimal Equivalents
The ability to convert fractions to decimals is crucial for various reasons:
-
Calculations: Decimals are often easier to work with in calculations, especially when using calculators or computers.
-
Comparisons: Comparing fractions can be challenging, but comparing decimals is much simpler. For example, comparing 1/3 and 2/5 is easier once converted to decimals (approximately 0.333 and 0.4).
-
Real-world applications: Many real-world measurements and quantities are expressed in decimals (e.g., prices, weights, lengths).
Frequently Asked Questions (FAQ)
Q1: Can all fractions be converted to terminating decimals?
No. Fractions with denominators that have prime factors other than 2 and 5 will result in repeating decimals. For example, 1/3 = 0.333... (a repeating decimal).
Q2: What if I have a fraction with a larger denominator?
The methods described above still apply. The division might require more steps, but the principle remains the same. You can use a calculator for larger numbers to aid in the division process.
Q3: Is there a shortcut for converting fractions with denominators that are powers of 10?
Yes, if the denominator is a power of 10 (10, 100, 1000, etc.), you can directly convert the fraction to a decimal by placing the numerator after the decimal point, with the number of decimal places equal to the number of zeros in the denominator. For example, 3/10 = 0.3, 27/100 = 0.27, and 456/1000 = 0.456.
Q4: Why is understanding this important for everyday life?
Many everyday tasks involve working with fractions and decimals. From calculating tips and discounts to measuring ingredients in recipes or understanding financial reports, the ability to convert between fractions and decimals is a valuable skill.
Conclusion
Converting 1 1/2 to its decimal equivalent, 1.5, is a straightforward process. We explored three distinct methods, each offering a unique perspective on the conversion. Understanding these methods extends beyond just this specific example and provides a strong foundation for handling various fraction-to-decimal conversions. The ability to seamlessly move between fractions and decimals is not merely a mathematical skill; it's a practical tool applicable to countless everyday situations. Remember to practice these methods with various fractions to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the easier it will become!
Latest Posts
Latest Posts
-
Gcf Of 30 And 16
Sep 16, 2025
-
What Is 100 Of 15
Sep 16, 2025
-
What Is 3 1
Sep 16, 2025
-
31 8 As A Mixed Number
Sep 16, 2025
-
Lcm Of 10 And 18
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 1 1/2 In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.