31/8 As A Mixed Number
keralas
Sep 16, 2025 · 5 min read
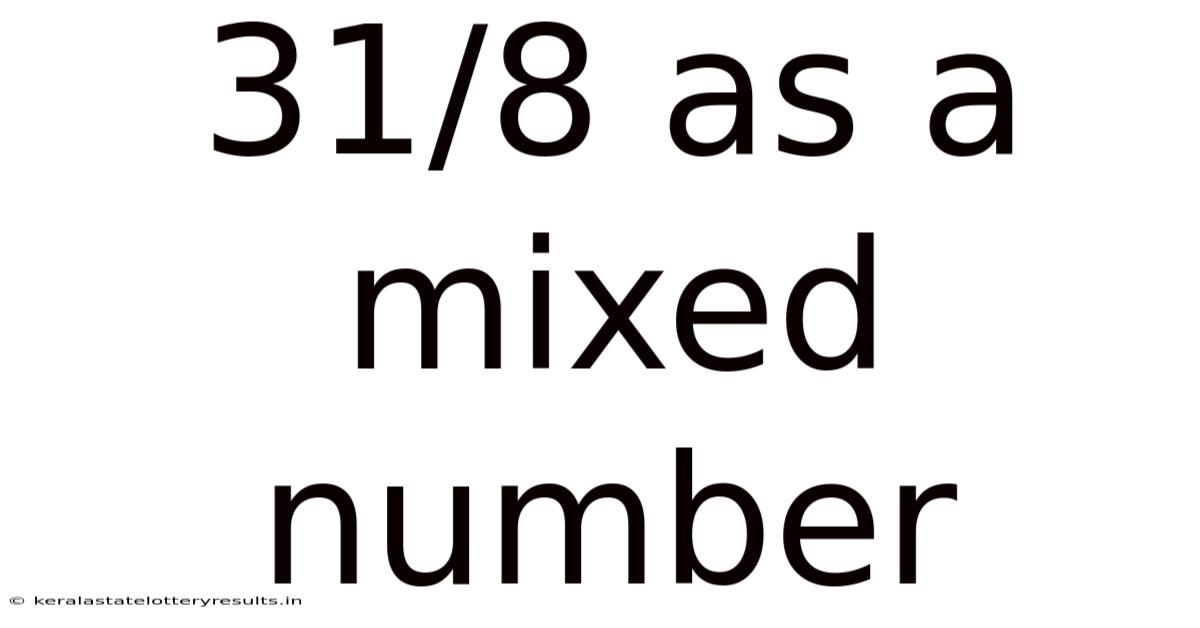
Table of Contents
Understanding 31/8 as a Mixed Number: A Comprehensive Guide
The fraction 31/8 represents a quantity larger than one whole. Understanding how to convert improper fractions like 31/8 into mixed numbers is a fundamental skill in mathematics, crucial for various applications from baking to engineering. This comprehensive guide will not only show you how to convert 31/8 to a mixed number but also why this process works, providing a solid foundation for future mathematical endeavors. We'll explore different methods, address common misconceptions, and even delve into the underlying mathematical principles.
What is a Mixed Number?
Before we dive into the conversion, let's define our terms. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ⅛ are all mixed numbers. They represent a quantity that is more than one whole unit but not a whole number itself.
Conversely, an improper fraction is a fraction where the numerator is greater than or equal to the denominator. Our example, 31/8, is an improper fraction because 31 (numerator) is larger than 8 (denominator). Improper fractions are perfectly valid representations of quantities, but mixed numbers are often preferred for their intuitive readability and ease of comparison.
Method 1: Long Division
The most straightforward method for converting an improper fraction to a mixed number involves long division. We divide the numerator by the denominator:
-
Divide: Divide 31 by 8. 8 goes into 31 three times (8 x 3 = 24).
-
Quotient: The quotient (the result of the division) becomes the whole number part of the mixed number. In this case, the quotient is 3.
-
Remainder: Subtract the product (24) from the dividend (31). The remainder is 7 (31 - 24 = 7).
-
Fraction: The remainder (7) becomes the numerator of the fraction, and the original denominator (8) remains the same.
-
Mixed Number: Therefore, 31/8 as a mixed number is 3 ⅞.
Method 2: Repeated Subtraction
This method offers a more visual understanding of the process. It's particularly helpful for those who find long division challenging.
-
Subtract the denominator: Start by subtracting the denominator (8) from the numerator (31) repeatedly until the result is less than the denominator.
- 31 - 8 = 23
- 23 - 8 = 15
- 15 - 8 = 7
-
Count the subtractions: Count how many times you subtracted the denominator. This is your whole number. We subtracted 8 three times.
-
Remainder as the numerator: The final result after repeated subtraction (7) is the remainder, which becomes the numerator of the fraction. The denominator remains the same (8).
-
Mixed Number: This gives us the mixed number 3 ⅞.
Visual Representation: Using Fraction Bars
Imagine you have 31 equal-sized pieces, and each group of 8 pieces forms one whole. You can arrange these pieces into groups of 8. You'll get three complete groups (3 wholes) and 7 pieces left over. These 7 pieces represent the remaining fraction, ⅞. This visual approach reinforces the concept of what a mixed number truly represents.
Why This Works: Mathematical Principles
The conversion from an improper fraction to a mixed number is based on the fundamental principle of representing the same quantity in different forms. Both 31/8 and 3 ⅞ represent the same numerical value. The process essentially decomposes the improper fraction into its whole number components and the remaining fractional part. The long division method is a streamlined approach to this decomposition.
Common Mistakes and How to Avoid Them
A common mistake is incorrectly calculating the remainder or forgetting to retain the original denominator. Always double-check your subtraction and ensure the denominator in the mixed number remains the same as in the original improper fraction. Another mistake is misinterpreting the whole number and the fraction – remember the whole number represents complete groups, while the fraction represents a part of a group.
Applications of Mixed Numbers
Mixed numbers are used extensively in everyday life and across various disciplines:
- Cooking and Baking: Recipes often use mixed numbers for ingredient quantities (e.g., 2 ½ cups of flour).
- Construction and Engineering: Measurements in construction frequently involve mixed numbers (e.g., 5 ⅝ inches).
- Data Analysis: Presenting data in mixed numbers can improve readability and understanding.
- Everyday Measurements: We commonly encounter mixed numbers when dealing with time (e.g., 1 hour and 15 minutes, or 1 ¼ hours) and length (e.g., 2 feet and 6 inches, or 2 ½ feet).
Expanding on the Concept: Further Exploration
Beyond simply converting 31/8, understanding the relationship between improper fractions and mixed numbers opens doors to more advanced concepts:
- Adding and Subtracting Mixed Numbers: Converting mixed numbers to improper fractions simplifies these operations.
- Multiplying and Dividing Mixed Numbers: Similar to addition and subtraction, conversion can ease these calculations.
- Comparing Fractions: Converting improper fractions to mixed numbers makes it easier to compare their relative sizes.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted into mixed numbers?
A: Yes, all improper fractions (where the numerator is greater than or equal to the denominator) can be converted into a mixed number or a whole number (if the numerator is a multiple of the denominator).
Q: What if the remainder is zero after the division?
A: If the remainder is zero, it means the improper fraction is equivalent to a whole number. For example, 16/8 = 2.
Q: Is it always necessary to convert improper fractions to mixed numbers?
A: Not always. Sometimes, improper fractions are more convenient for calculations, particularly in algebra. However, mixed numbers are usually preferred for representing quantities in everyday contexts.
Q: Are there other ways to represent 31/8?
A: Yes, 31/8 can also be represented as a decimal (3.875). The choice of representation depends on the context and the desired level of precision.
Conclusion
Converting 31/8 to the mixed number 3 ⅞ is a fundamental skill that has broad applicability. By understanding the underlying principles and different methods, you'll not only master this specific conversion but also develop a deeper understanding of fractions, paving the way for more complex mathematical concepts. Remember to practice regularly, explore different methods, and always double-check your calculations to build confidence and accuracy. This skill, seemingly simple, forms a cornerstone of further mathematical exploration and real-world application. Mastering it now will undoubtedly benefit you in your future academic and professional endeavors.
Latest Posts
Latest Posts
-
Lcm Of 16 And 36
Sep 16, 2025
-
Gcf Of 12 And 44
Sep 16, 2025
-
What Times What Equals 85
Sep 16, 2025
-
Convert 0 125 Into A Fraction
Sep 16, 2025
-
What Is 28 Square Root
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 31/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.