What Is 100 Of 15
keralas
Sep 16, 2025 · 5 min read
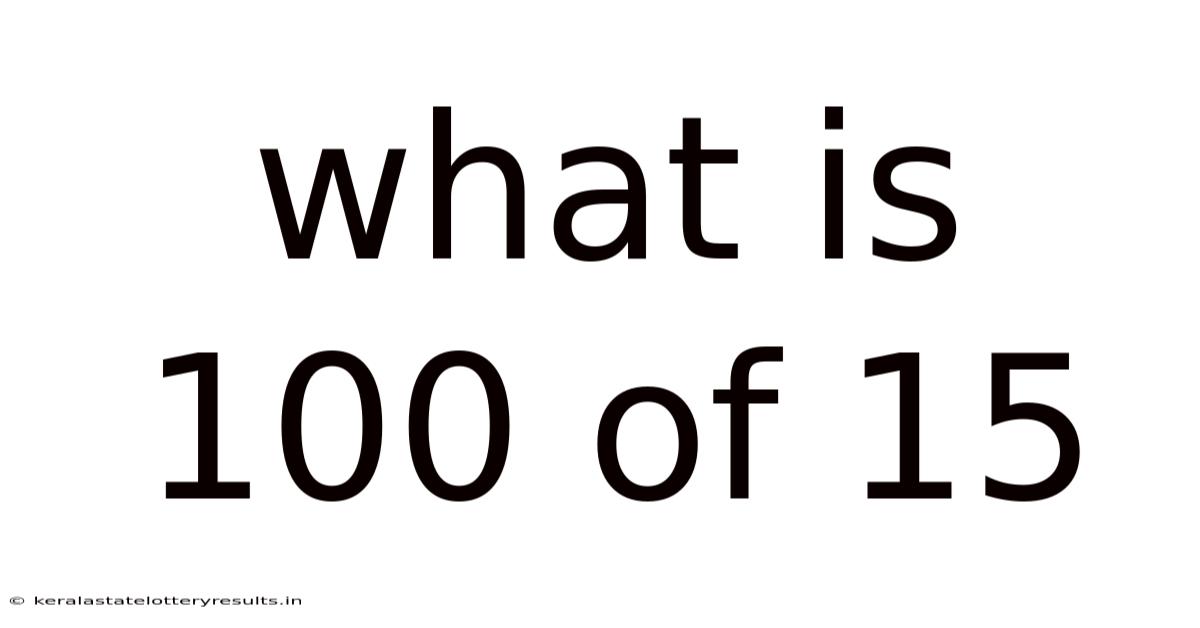
Table of Contents
What is 100% of 15? Understanding Percentages and Their Applications
This article explores the seemingly simple question: "What is 100% of 15?" While the answer might seem immediately obvious, delving into the concept provides a valuable opportunity to understand percentages, their fundamental principles, and their wide-ranging applications in various fields. We'll move beyond a simple calculation to explore the underlying mathematical concepts, practical examples, and common misconceptions surrounding percentages.
Introduction: The Basics of Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, 100% of any number represents the whole, the entirety of that number. So, 100% of 15 is simply 15. This seems straightforward, but understanding the underlying principles allows us to tackle more complex percentage problems.
Calculating 100% of 15: A Step-by-Step Approach
The calculation is elementary:
- Identify the whole: In this case, the whole is 15.
- Express the percentage as a decimal: 100% is equivalent to 1.00 or simply 1.
- Multiply the whole by the decimal: 15 x 1 = 15.
Therefore, 100% of 15 is 15.
While this specific calculation is trivial, understanding this process forms the foundation for solving more complex percentage problems. Let's explore how this basic principle extends to more challenging scenarios.
Beyond the Basics: Working with Other Percentages
The method used to calculate 100% of 15 can be adapted to find any percentage of any number. Let's consider a few examples:
-
Finding 50% of 15: 50% is equivalent to 0.50 or 1/2. Therefore, 50% of 15 is 15 x 0.50 = 7.5.
-
Finding 25% of 15: 25% is equivalent to 0.25 or 1/4. Therefore, 25% of 15 is 15 x 0.25 = 3.75.
-
Finding 150% of 15: 150% is equivalent to 1.50 or 3/2. Therefore, 150% of 15 is 15 x 1.50 = 22.5. This illustrates that percentages can exceed 100%, representing more than the whole.
Practical Applications of Percentages
Percentages are ubiquitous in everyday life and across numerous professional fields. Here are some examples:
-
Sales and discounts: Stores often advertise discounts as percentages (e.g., "20% off"). Understanding percentages is crucial for calculating the final price after a discount.
-
Financial calculations: Interest rates on loans and savings accounts are expressed as percentages. Calculating interest earned or paid requires a solid grasp of percentage calculations.
-
Statistics and data analysis: Percentages are frequently used to represent proportions in data sets. For instance, survey results are often presented as percentages to show the distribution of responses.
-
Science and engineering: Percentages are used to express efficiency, error margins, and changes in quantities.
-
Cooking and baking: Recipes often specify ingredients as percentages of the total weight or volume.
Understanding Percentage Increase and Decrease
Calculating percentage increases and decreases is another crucial application. Consider these examples:
-
Percentage increase: If a value increases from 10 to 15, the percentage increase is calculated as follows:
- Find the difference: 15 - 10 = 5
- Divide the difference by the original value: 5 / 10 = 0.5
- Multiply by 100 to express as a percentage: 0.5 x 100 = 50%
Therefore, the value increased by 50%.
-
Percentage decrease: If a value decreases from 20 to 15, the percentage decrease is calculated as follows:
- Find the difference: 20 - 15 = 5
- Divide the difference by the original value: 5 / 20 = 0.25
- Multiply by 100 to express as a percentage: 0.25 x 100 = 25%
Therefore, the value decreased by 25%.
Common Misconceptions about Percentages
Several common misconceptions surround percentages that can lead to errors in calculations:
-
Adding percentages directly: It's incorrect to simply add percentages without considering the base value. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Confusing percentage change with absolute change: A large percentage change doesn't necessarily mean a large absolute change, and vice versa. A 10% increase on a small base value is much smaller than a 10% increase on a large base value.
-
Incorrectly interpreting percentages in context: Always carefully consider the context in which a percentage is presented. The same percentage can represent vastly different quantities depending on the base value.
Advanced Percentage Calculations and Applications
While this article focuses on the fundamentals, it's important to acknowledge the existence of more advanced percentage calculations and applications. These include:
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding compound interest is crucial for long-term financial planning.
-
Percentage points: This refers to the arithmetic difference between two percentages. For instance, an increase from 10% to 15% is a 5 percentage point increase, not a 50% increase.
-
Weighted averages: These are used when different values contribute differently to the overall average. For example, calculating a weighted average grade in a course where assignments have different weights.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a percentage and a proportion?
- A: A percentage is a special type of proportion expressed as a fraction of 100. A proportion is a more general term that represents the relative size of one part compared to the whole.
-
Q: How do I convert a fraction to a percentage?
- A: To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100.
-
Q: How do I convert a decimal to a percentage?
- A: To convert a decimal to a percentage, multiply the decimal by 100 and add the percent sign (%).
Conclusion: The Power of Understanding Percentages
While finding 100% of 15 might seem trivial, understanding the underlying principles of percentages empowers us to solve a wide variety of problems in everyday life, professional settings, and various fields of study. From calculating discounts to analyzing financial data, understanding percentages is a fundamental skill with far-reaching applications. This article has provided a comprehensive introduction, moving beyond the simple calculation to explore the deeper concepts, practical applications, and common misconceptions associated with percentages. Mastering these principles opens doors to a deeper understanding of the quantitative world around us.
Latest Posts
Latest Posts
-
Gcf Of 12 And 44
Sep 16, 2025
-
What Times What Equals 85
Sep 16, 2025
-
Convert 0 125 Into A Fraction
Sep 16, 2025
-
What Is 28 Square Root
Sep 16, 2025
-
What Is 108 Divisible By
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 100 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.