What Is -3 - 1
keralas
Sep 16, 2025 · 6 min read
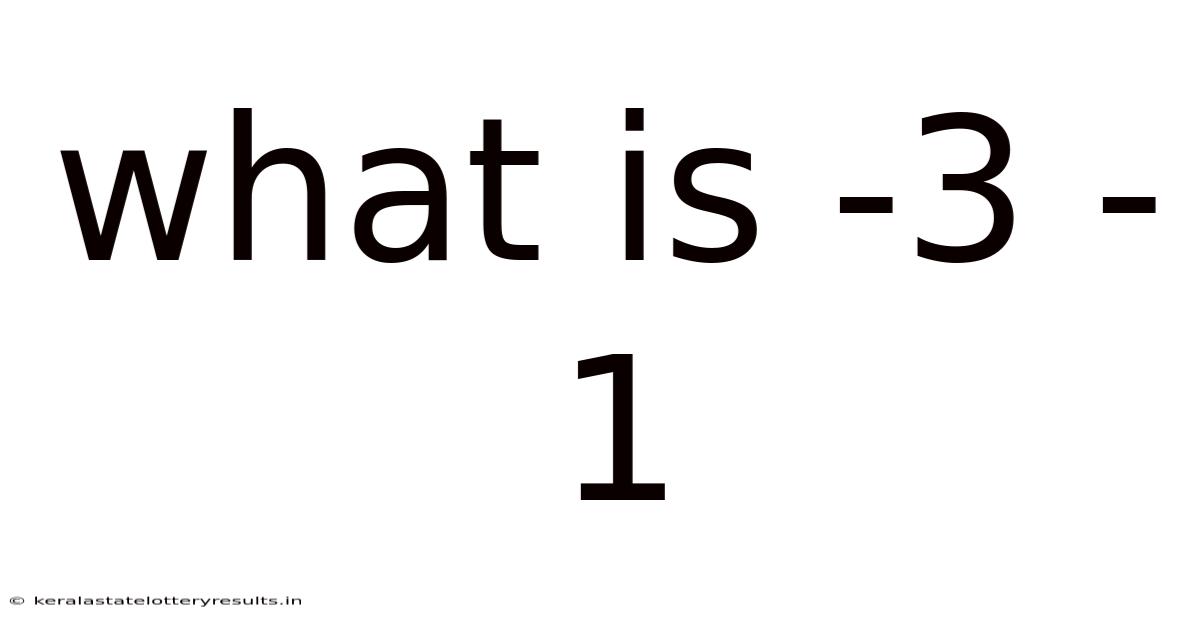
Table of Contents
What is -3 - 1? Understanding Negative Numbers and Subtraction
This article delves into the seemingly simple question: What is -3 - 1? While the answer might seem obvious to some, understanding the underlying principles of subtracting negative numbers is crucial for a solid grasp of arithmetic and algebra. We will explore the concept of negative numbers, explain the process of subtraction with negative numbers, and provide various perspectives to solidify your understanding. This will involve looking at the number line, using different models, and addressing common misconceptions. By the end, you'll not only know the answer but also understand why the answer is what it is.
Introduction to Negative Numbers
Before tackling the subtraction problem, let's establish a firm understanding of negative numbers. Negative numbers are numbers less than zero. They are often used to represent quantities below a reference point, such as temperature below zero degrees Celsius or a debt in financial contexts. They are represented with a minus sign (-) before the number. For example, -5 represents a quantity five units less than zero.
Imagine a number line:
... -5 -4 -3 -2 -1 0 1 2 3 4 5 ...
Zero is the midpoint, with positive numbers extending to the right and negative numbers extending to the left. The further a number is from zero to the left, the smaller its value. Therefore, -5 is smaller than -3, which is smaller than -1, and so on.
Understanding Subtraction
Subtraction can be interpreted in a few ways. One common understanding is "taking away." If you have 5 apples and subtract 2, you are taking away 2 apples, leaving you with 3. However, this "taking away" model becomes less intuitive when dealing with negative numbers.
A more general and useful way to think about subtraction is as the inverse of addition. Subtracting a number is the same as adding its opposite. The opposite of a positive number is its negative counterpart (e.g., the opposite of 5 is -5), and the opposite of a negative number is its positive counterpart (e.g., the opposite of -3 is 3).
Solving -3 - 1: A Step-by-Step Approach
Now, let's apply this understanding to solve -3 - 1.
-
Identify the operation: We are performing subtraction.
-
Rewrite as addition: Subtracting 1 is the same as adding its opposite, which is -1. Therefore, -3 - 1 can be rewritten as -3 + (-1).
-
Perform the addition: We are now adding two negative numbers. When adding numbers with the same sign (both negative in this case), we add their absolute values and keep the negative sign. The absolute value of -3 is 3, and the absolute value of -1 is 1. Adding 3 and 1 gives us 4. Therefore, -3 + (-1) = -4.
Therefore, -3 - 1 = -4
Visualizing with the Number Line
The number line provides a visual representation of this process. Starting at -3, subtracting 1 means moving one unit to the left on the number line. This brings us to -4.
... -5 -4 -3 -2 -1 0 1 2 3 4 5 ...
^ ^
| |
| | Subtracting 1 from -3 means moving one unit to the left.
|-3 |-4
Using the Debt Analogy
A helpful analogy involves debt. Think of -3 as representing a debt of 3 units. Subtracting 1 means adding to your debt, increasing it by 1 unit. This results in a total debt of 4 units, represented as -4.
Addressing Common Misconceptions
A frequent mistake is treating -3 - 1 as if it were -3 + 1. Remember, subtracting a number is not the same as adding it. Subtracting 1 moves you to the left on the number line, whereas adding 1 moves you to the right.
Another common misunderstanding involves the signs. Students often incorrectly change the signs of both numbers when dealing with subtraction of negative numbers. Remember, only the sign of the number being subtracted changes when you rewrite the subtraction as addition.
Expanding the Concept: Subtracting More Complex Negative Numbers
Let's consider a slightly more complex example: -5 - (-2).
-
Rewrite as addition: Subtracting a negative number is equivalent to adding its positive counterpart. So, -5 - (-2) becomes -5 + 2.
-
Perform the addition: We are adding numbers with different signs. In this case, we subtract the smaller absolute value (2) from the larger absolute value (5), and keep the sign of the number with the larger absolute value (negative). 5 - 2 = 3, and the larger absolute value is negative, so -5 + 2 = -3.
Therefore, -5 - (-2) = -3
This example demonstrates that subtracting a negative number results in a movement to the right on the number line. It's essentially the same as adding a positive number.
Mathematical Explanation and Properties
The operation of subtraction can be described mathematically as the addition of the additive inverse. The additive inverse of a number 'a' is denoted as -a. This means that a + (-a) = 0.
So, when we subtract a number, we're actually adding its additive inverse. This concept holds true for both positive and negative numbers. The properties of addition, such as the associative and commutative properties, don't directly apply to subtraction, but they apply to the equivalent addition operation after rewriting the subtraction expression.
Frequently Asked Questions (FAQ)
-
Q: Why does subtracting a negative number result in addition?
- A: Subtracting a number is equivalent to adding its opposite. The opposite of a negative number is positive.
-
Q: Can I use a calculator to solve these problems?
- A: Yes, calculators can handle negative numbers and subtraction effectively. However, understanding the underlying principles is essential for problem-solving beyond simple calculations.
-
Q: Are there other ways to represent or visualize subtraction with negative numbers?
- A: Yes, various models, including using colored chips (red for negative, black for positive), can help visualize the process.
-
Q: What if I have more than two numbers involved in the subtraction?
- A: You can still apply the same principles. Rewrite all subtractions as additions of opposites and then proceed with addition following the rules of combining positive and negative numbers.
Conclusion: Mastering Negative Number Subtraction
Understanding subtraction involving negative numbers is a cornerstone of mathematical proficiency. By viewing subtraction as the addition of the opposite and visualizing the process on a number line, we can overcome the challenges presented by negative numbers. The debt analogy and other visualization methods can further solidify this understanding. Mastering these concepts is not just about getting the right answer but about developing a deep and intuitive grasp of fundamental mathematical principles. Remember, practice is key! Work through several examples, using different methods to reinforce your understanding and build confidence in tackling more complex problems involving negative numbers. The seemingly simple question of "-3 - 1" opens a door to a much wider understanding of number systems and arithmetic operations.
Latest Posts
Latest Posts
-
Lcm Of 16 And 36
Sep 16, 2025
-
Gcf Of 12 And 44
Sep 16, 2025
-
What Times What Equals 85
Sep 16, 2025
-
Convert 0 125 Into A Fraction
Sep 16, 2025
-
What Is 28 Square Root
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is -3 - 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.