What Is 45 Of 20
keralas
Sep 15, 2025 · 5 min read
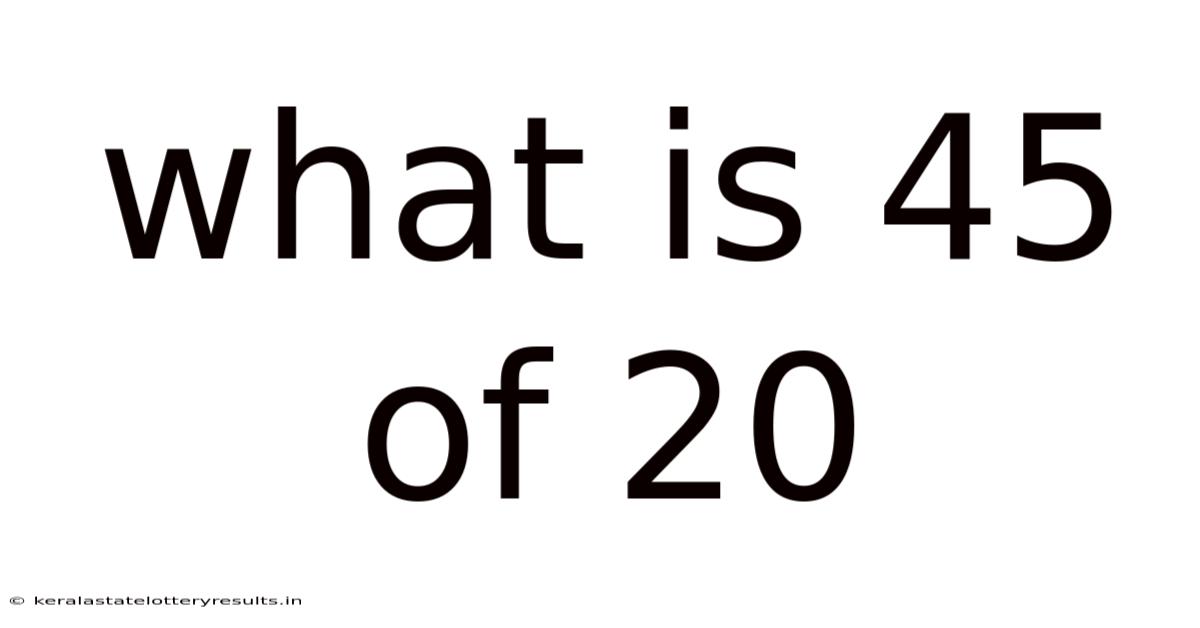
Table of Contents
What is 45% of 20? A Deep Dive into Percentages and Practical Applications
Finding 45% of 20 might seem like a simple calculation, but it opens a door to understanding percentages – a crucial concept in various aspects of life, from everyday budgeting to complex financial modeling. This article will not only show you how to calculate 45% of 20 but also explore the underlying principles, different calculation methods, and real-world applications of percentages.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" denotes percentage. So, 45% means 45 out of 100, or 45/100, which can be simplified to 9/20. Understanding this fundamental definition is key to solving percentage problems. We will explore several ways to calculate 45% of 20, catering to different levels of mathematical understanding.
Method 1: Converting Percentage to Decimal
This is the most straightforward method. We convert the percentage into a decimal by dividing it by 100. Then, we multiply the decimal by the number we're finding the percentage of.
- Step 1: Convert 45% to a decimal: 45% / 100 = 0.45
- Step 2: Multiply the decimal by 20: 0.45 * 20 = 9
Therefore, 45% of 20 is 9.
Method 2: Using Fractions
As mentioned earlier, 45% can be expressed as the fraction 45/100. We can then use this fraction to calculate 45% of 20.
- Step 1: Express 45% as a fraction: 45/100
- Step 2: Multiply the fraction by 20: (45/100) * 20 = 900/100
- Step 3: Simplify the fraction: 900/100 = 9
Again, we arrive at the answer: 45% of 20 is 9.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. We set up a proportion where we relate the percentage to the whole.
- Step 1: Set up the proportion: 45/100 = x/20 (where x is 45% of 20)
- Step 2: Cross-multiply: 45 * 20 = 100 * x
- Step 3: Solve for x: 900 = 100x => x = 900/100 = 9
This method, while slightly more involved, reinforces the fundamental relationship between percentages, parts, and wholes.
Method 4: Using a Calculator
Most calculators have a percentage function. Simply enter 45, press the "%" button, then multiply by 20. The calculator will automatically perform the necessary conversion and calculation. This is a quick and convenient method for everyday use.
A Deeper Dive into Percentages: Mathematical Principles
The ability to calculate percentages relies on a strong understanding of fractions, decimals, and proportions. These mathematical concepts are interconnected and form the foundation of many advanced mathematical applications.
-
Fractions: Percentages are essentially fractions with a denominator of 100. Converting between percentages and fractions helps simplify calculations and deepen understanding. For example, understanding that 45% is equivalent to 9/20 allows for easier mental calculations in some scenarios.
-
Decimals: Decimals provide a convenient way to represent percentages in calculations. The conversion process (dividing by 100) is straightforward and readily applicable in various mathematical contexts. Working with decimals is crucial for many calculations, including those involving money, measurements, and scientific data.
-
Proportions: Proportions demonstrate the relationship between two ratios. The proportion method for calculating percentages emphasizes the core concept of relative magnitude. Understanding proportions is crucial for solving many real-world problems involving scaling, ratios, and rates.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives, appearing in various contexts:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. Understanding percentages is essential for making sound financial decisions and managing personal finances effectively.
-
Shopping: Discounts and sales are often expressed as percentages. The ability to quickly calculate the final price after a discount helps in making informed purchasing decisions.
-
Science: Percentages are used to express concentrations of solutions, statistical probabilities, and error margins in experiments. Accurate percentage calculations are vital for maintaining accuracy and reliability in scientific research.
-
Data Analysis: Percentages are widely used to represent data and trends in graphs, charts, and reports. Understanding percentages helps to interpret data effectively and draw meaningful conclusions.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and comparing prices of different products all involve percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage of a number that isn't a whole number? A: The methods described above work equally well for whole numbers and decimals. Simply substitute the decimal number into the calculations.
-
Q: How can I improve my mental math skills with percentages? A: Practice regularly with simple percentage problems. Memorize common percentage-to-fraction conversions (e.g., 50% = 1/2, 25% = 1/4, 10% = 1/10). Break down complex calculations into smaller, manageable steps.
-
Q: Are there any online tools or calculators for percentage calculations? A: Yes, many websites and apps offer percentage calculators. These can be helpful for quick calculations or for verifying your manual work.
-
Q: What if I need to calculate the percentage one number represents of another? A: To find what percentage number A is of number B, you use the formula: (A/B) * 100%. For example, to find what percentage 9 is of 20, you would calculate (9/20) * 100% = 45%.
Conclusion: Mastering Percentages
Understanding and calculating percentages is a fundamental skill applicable across various disciplines and everyday situations. While calculating 45% of 20 might seem trivial, the underlying principles and methods explored in this article empower you to tackle more complex percentage problems. By mastering these concepts, you not only improve your mathematical proficiency but also enhance your ability to analyze data, make informed decisions, and navigate various aspects of life with greater confidence. Remember, the key is practice and understanding the fundamental relationships between percentages, fractions, decimals, and proportions. The more you practice, the easier and more intuitive these calculations will become.
Latest Posts
Latest Posts
-
Y 3 X 3 2
Sep 16, 2025
-
Is 15 An Odd Number
Sep 16, 2025
-
Coefficient Of Variation In Excel
Sep 16, 2025
-
What Is 1 4 1
Sep 16, 2025
-
130 Miles In Km H
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 45 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.