Y 3 X 3 2
keralas
Sep 16, 2025 · 5 min read
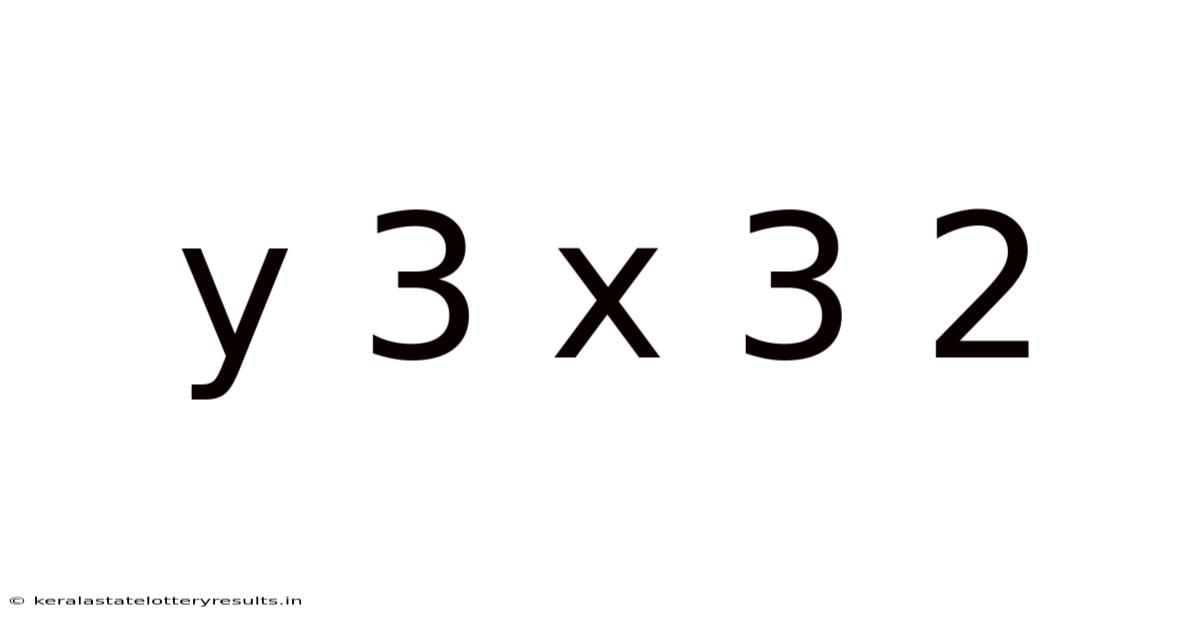
Table of Contents
Decoding the Mathematical Expression: y = 3x³ + 2
This article delves into the mathematical expression y = 3x³ + 2, exploring its properties, applications, and significance in various mathematical contexts. We'll cover its graphical representation, how to solve for x and y, and touch upon its broader implications in fields like calculus and physics. Understanding this seemingly simple equation provides a strong foundation for more complex mathematical concepts.
Introduction: Understanding the Basics
The equation y = 3x³ + 2 represents a cubic function. A cubic function is a polynomial function of degree three, meaning the highest power of the variable x is 3. The equation consists of three main components:
- y: The dependent variable. Its value depends on the value of x.
- x: The independent variable. We can choose any value for x, and the equation will give us the corresponding value of y.
- 3x³: The cubic term. This term dominates the function's behavior for large values of x.
- 2: The constant term. This term shifts the entire graph vertically.
Graphical Representation: Visualizing the Function
The graph of y = 3x³ + 2 is a curve, characteristic of cubic functions. It exhibits the following key features:
- Increasing Function: As x increases, y also increases. This means the function is monotonically increasing.
- No Maximum or Minimum Values: Unlike quadratic functions (parabolas), cubic functions generally do not have a single maximum or minimum point. They can have inflection points, where the concavity changes.
- One Real Root: The equation 3x³ + 2 = 0 has one real root and two complex roots. This real root represents the x-intercept (where the graph crosses the x-axis). We can approximate this root using numerical methods.
- Vertical Shift: The "+2" term shifts the entire graph two units upward compared to the graph of y = 3x³.
Solving for y: Finding the Output
Solving for y is straightforward. Given a value for x, simply substitute it into the equation and perform the calculations. For example:
- If x = 1, then y = 3(1)³ + 2 = 5.
- If x = 2, then y = 3(2)³ + 2 = 26.
- If x = -1, then y = 3(-1)³ + 2 = -1.
- If x = 0, then y = 3(0)³ + 2 = 2.
This shows how different values of x produce different values of y, illustrating the function's behavior.
Solving for x: Finding the Input
Solving for x, when y is known, requires a bit more work. We need to solve the cubic equation:
3x³ + 2 = y
This can be rewritten as:
3x³ = y - 2
x³ = (y - 2) / 3
x = ³√((y - 2) / 3)
The cube root operation (³√) always yields one real root. For example:
- If y = 5, then x = ³√((5 - 2) / 3) = ³√1 = 1.
- If y = 26, then x = ³√((26 - 2) / 3) = ³√8 = 2.
- If y = -1, then x = ³√((-1 - 2) / 3) = ³√(-1) = -1.
This process demonstrates how to find the input (x) given a specific output (y).
Calculus Applications: Exploring Derivatives and Integrals
The power of calculus allows for a deeper understanding of the cubic function.
- First Derivative: The first derivative, dy/dx, represents the slope of the tangent line at any point on the curve. For y = 3x³ + 2, the first derivative is: dy/dx = 9x². This shows the slope is always non-negative (positive or zero), confirming the monotonically increasing nature of the function.
- Second Derivative: The second derivative, d²y/dx², represents the concavity of the curve. For y = 3x³ + 2, the second derivative is: d²y/dx² = 18x. This indicates that the concavity changes at x = 0; the function is concave down for x < 0 and concave up for x > 0. This point (x=0, y=2) is the inflection point.
- Integration: Integrating the function allows us to find the area under the curve. The indefinite integral of 3x³ + 2 is: (3/4)x⁴ + 2x + C, where C is the constant of integration. This integral has applications in various fields, such as calculating the work done by a force or the volume of a solid of revolution.
Applications in Physics and Engineering:
Cubic functions appear in various physical phenomena and engineering applications. For instance:
- Projectile Motion: While simplified models often use quadratic functions, more accurate models of projectile motion, considering air resistance, can involve cubic or higher-order functions.
- Fluid Dynamics: The relationship between flow rate and pressure in certain fluid systems can be described by cubic equations.
- Mechanical Engineering: Cubic functions can model the deflection of beams under load or the relationship between stress and strain in some materials.
Frequently Asked Questions (FAQ)
-
Q: What is the domain of the function y = 3x³ + 2?
- A: The domain is all real numbers (-∞, +∞). We can substitute any real number for x and obtain a real number for y.
-
Q: What is the range of the function y = 3x³ + 2?
- A: The range is also all real numbers (-∞, +∞). Since the function is monotonically increasing and unbounded, it covers all possible y-values.
-
Q: How can I find the inflection point of the function?
- A: The inflection point occurs where the second derivative is zero and changes sign. In this case, d²y/dx² = 18x = 0, so x = 0. Substituting x = 0 into the original equation gives y = 2. Therefore, the inflection point is (0, 2).
-
Q: Can this function be used to model real-world phenomena?
- A: Yes, as discussed above, cubic functions have applications in physics, engineering, and other fields. However, the specific context determines whether this particular cubic function (y = 3x³ + 2) is an appropriate model.
Conclusion: The Significance of Understanding Cubic Functions
The seemingly simple equation y = 3x³ + 2 opens a window into the rich world of cubic functions. Understanding its properties, graphing techniques, and the ability to solve for x and y forms a crucial stepping stone in grasping more complex mathematical concepts. Its applications in various scientific and engineering fields highlight the practical importance of mastering these fundamental mathematical principles. By exploring this equation thoroughly, we not only gain a deeper understanding of mathematics but also develop valuable problem-solving skills applicable to a wide range of challenges. The journey from a basic equation to its multifaceted applications underscores the power of mathematical modeling and its ability to describe and predict real-world phenomena.
Latest Posts
Latest Posts
-
What Is 20 Of 80 00
Sep 16, 2025
-
70km To Miles Per Hour
Sep 16, 2025
-
Triangular Prism Vs Triangular Pyramid
Sep 16, 2025
-
33 Cm How Many Inches
Sep 16, 2025
-
5 8 Of An Inch
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Y 3 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.