Lcm Of 15 And 8
keralas
Sep 17, 2025 · 6 min read
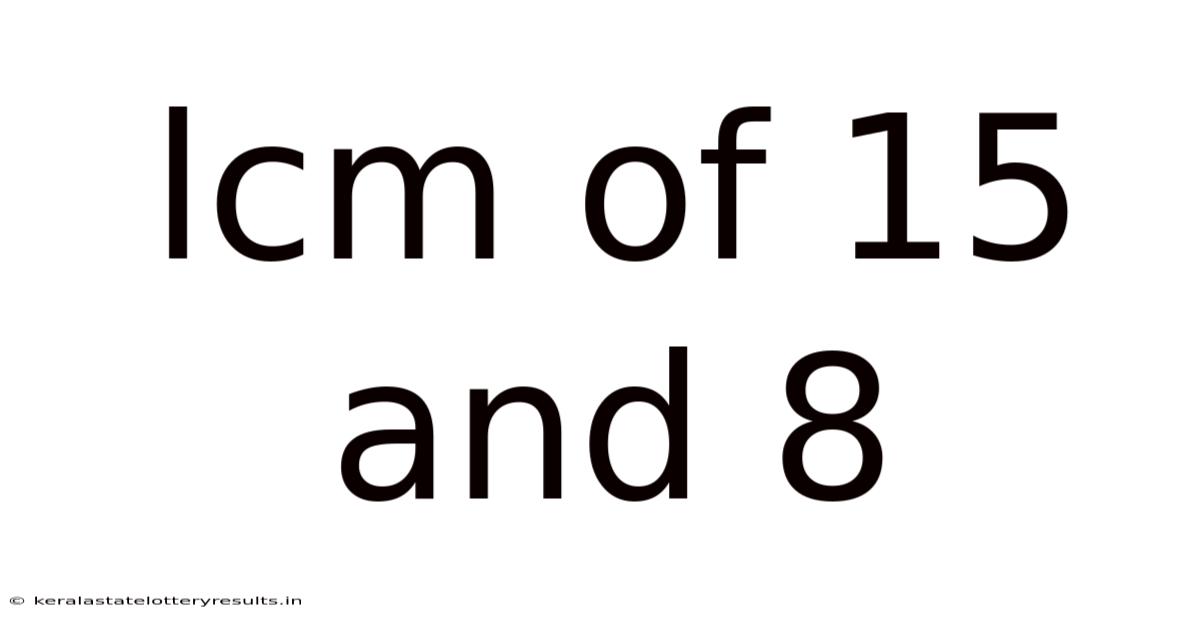
Table of Contents
Finding the Least Common Multiple (LCM) of 15 and 8: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts is crucial for grasping more advanced mathematical ideas. This comprehensive guide will not only show you how to calculate the LCM of 15 and 8 but also delve into the theory behind it, exploring different methods and their applications. We'll equip you with the knowledge to tackle similar problems with confidence and even explain why this seemingly simple concept is so important.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers you're considering as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3. This concept is fundamental in various areas of mathematics, including fractions, algebra, and even more advanced fields.
Method 1: Listing Multiples
The most straightforward method for finding the LCM of relatively small numbers like 15 and 8 is by listing their multiples. Let's start by listing the multiples of 15 and 8:
Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150...
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128...
By comparing the two lists, we can identify the smallest number that appears in both: 120. Therefore, the LCM of 15 and 8 is 120.
This method is easy to visualize and understand, especially for beginners. However, it becomes less practical when dealing with larger numbers or more than two numbers, as the lists can get quite extensive.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, is using prime factorization. This involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorization of 15: 3 x 5
- Prime factorization of 8: 2 x 2 x 2 = 2³
To find the LCM using prime factorization, we follow these steps:
- Identify all the prime factors present in the numbers: In our case, we have 2, 3, and 5.
- For each prime factor, select the highest power: The highest power of 2 is 2³, the highest power of 3 is 3¹, and the highest power of 5 is 5¹.
- Multiply the selected highest powers together: 2³ x 3 x 5 = 8 x 3 x 5 = 120
Therefore, the LCM of 15 and 8 is 120. This method is significantly faster and more efficient than listing multiples, especially when dealing with larger numbers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both integers without leaving a remainder. There's a convenient formula that links the LCM and GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
Let's find the GCD of 15 and 8 using the Euclidean algorithm:
- Divide the larger number (15) by the smaller number (8): 15 = 1 x 8 + 7
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (7): 8 = 1 x 7 + 1
- Repeat the process: 7 = 7 x 1 + 0
The GCD is the last non-zero remainder, which is 1.
Now, we can use the formula:
LCM(15, 8) x GCD(15, 8) = 15 x 8 LCM(15, 8) x 1 = 120 LCM(15, 8) = 120
This method elegantly connects the concepts of LCM and GCD, providing another efficient way to calculate the LCM. The Euclidean algorithm is particularly useful for finding the GCD of larger numbers.
Why is Finding the LCM Important?
The LCM isn't just an abstract mathematical concept; it has practical applications in various scenarios:
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is crucial for finding a common denominator. This simplifies the calculation significantly. For example, adding 1/15 and 1/8 requires finding the LCM of 15 and 8 (which is 120) to get a common denominator.
-
Scheduling: LCM finds applications in scheduling problems. Imagine two events that repeat at different intervals. For example, one event occurs every 15 days, and another every 8 days. The LCM (120 days) tells us when both events will occur on the same day again.
-
Modular Arithmetic: In modular arithmetic (a branch of number theory), the LCM plays a significant role in solving congruence problems.
-
Real-world applications: LCM concepts are used in various engineering and manufacturing processes, particularly when dealing with cyclical operations or synchronizing different machinery working at different speeds.
Frequently Asked Questions (FAQ)
Q1: What if I have more than two numbers? How do I find the LCM?
A1: You can extend the prime factorization method or the GCD-based method to handle more than two numbers. For prime factorization, you simply consider all the prime factors from all the numbers and choose the highest power of each. For the GCD-based method, you can find the LCM iteratively, first finding the LCM of two numbers, then finding the LCM of the result and the next number, and so on.
Q2: Are there any other methods for finding the LCM?
A2: Yes, there are other, less common methods, such as using Venn diagrams for visualizing prime factors or employing specialized algorithms for very large numbers. However, the methods discussed above (listing multiples, prime factorization, and the GCD method) are the most efficient and widely used.
Q3: What if one of the numbers is zero?
A3: The LCM of any number and 0 is undefined. This is because 0 is a multiple of every integer, and there's no smallest positive integer divisible by all the integers if one of them is 0.
Q4: Can the LCM of two numbers be equal to one of the numbers?
A4: Yes, this happens if one number is a multiple of the other. For example, the LCM of 15 and 30 is 30.
Conclusion
Finding the least common multiple (LCM) is a fundamental concept in mathematics with significant applications in various fields. While seemingly simple, a thorough understanding of the underlying principles and the various methods for calculating the LCM equips you with valuable problem-solving skills. We've explored three primary methods – listing multiples, prime factorization, and utilizing the greatest common divisor – each with its strengths and weaknesses, allowing you to choose the most appropriate method depending on the numbers involved. Remember, mastering the LCM is not just about getting the right answer; it's about understanding the mathematical concepts that underpin it and appreciating its relevance in various contexts. With practice and a clear understanding of these concepts, you'll be able to confidently tackle LCM problems and further your mathematical journey.
Latest Posts
Latest Posts
-
Gcf Of 45 And 18
Sep 17, 2025
-
What Is Xviii In Numbers
Sep 17, 2025
-
Is 40 Prime Or Composite
Sep 17, 2025
-
Gcf Of 12 And 14
Sep 17, 2025
-
Lcm Of 20 And 16
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.