Lcm Of 20 And 16
keralas
Sep 17, 2025 · 6 min read
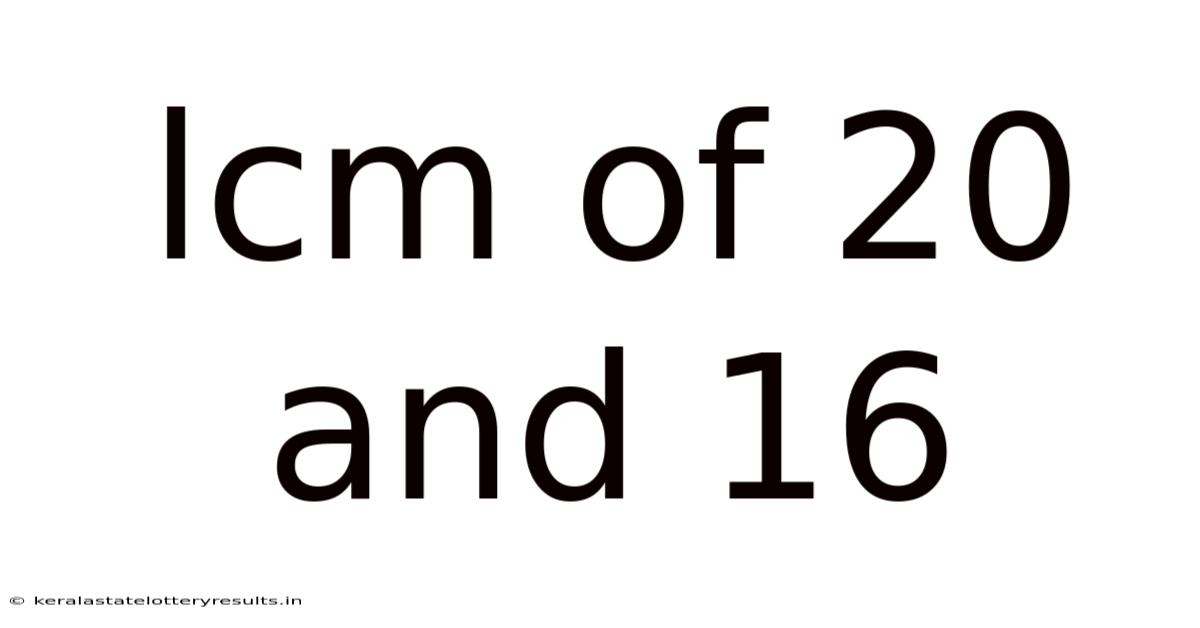
Table of Contents
Finding the Least Common Multiple (LCM) of 20 and 16: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it offers valuable insights into number theory. This article will delve deep into finding the LCM of 20 and 16, exploring various approaches and explaining the mathematical principles involved. We will cover the prime factorization method, the listing multiples method, and the greatest common divisor (GCD) method, equipping you with a comprehensive understanding of this fundamental concept.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder. Understanding LCM is crucial in various mathematical applications, including simplifying fractions, solving problems involving ratios and proportions, and scheduling repetitive events. This article focuses on finding the LCM of 20 and 16, demonstrating different methods and providing a solid foundation for understanding this key mathematical concept.
Method 1: Prime Factorization
This method is considered one of the most efficient ways to find the LCM, especially when dealing with larger numbers. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply to give the original number.
Step 1: Find the prime factorization of each number.
- 20 = 2 x 2 x 5 = 2² x 5
- 16 = 2 x 2 x 2 x 2 = 2⁴
Step 2: Identify the highest power of each prime factor present in the factorizations.
In our case, the prime factors are 2 and 5.
- The highest power of 2 is 2⁴ = 16
- The highest power of 5 is 5¹ = 5
Step 3: Multiply the highest powers of all prime factors together.
LCM(20, 16) = 2⁴ x 5 = 16 x 5 = 80
Therefore, the least common multiple of 20 and 16 is 80. This means that 80 is the smallest positive integer that is divisible by both 20 and 16.
Method 2: Listing Multiples
This method is straightforward but can be less efficient for larger numbers. It involves listing the multiples of each number until you find the smallest common multiple.
Step 1: List the multiples of 20.
Multiples of 20: 20, 40, 60, 80, 100, 120, 140, 160...
Step 2: List the multiples of 16.
Multiples of 16: 16, 32, 48, 64, 80, 96, 112, 128...
Step 3: Identify the smallest common multiple.
By comparing the lists, we see that the smallest multiple that appears in both lists is 80.
Therefore, the LCM(20, 16) = 80.
Method 3: Using the Greatest Common Divisor (GCD)
This method utilizes the relationship between the LCM and the greatest common divisor (GCD) of two numbers. The GCD is the largest positive integer that divides both numbers without leaving a remainder. The formula connecting LCM and GCD is:
LCM(a, b) = (|a x b|) / GCD(a, b)
where 'a' and 'b' are the two numbers.
Step 1: Find the GCD of 20 and 16 using the Euclidean algorithm.
The Euclidean algorithm is an efficient method to find the GCD.
- Divide the larger number (20) by the smaller number (16): 20 ÷ 16 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (16) and the smaller number with the remainder (4).
- Repeat the process: 16 ÷ 4 = 4 with a remainder of 0.
- The GCD is the last non-zero remainder, which is 4.
Therefore, GCD(20, 16) = 4.
Step 2: Apply the LCM formula.
LCM(20, 16) = (|20 x 16|) / GCD(20, 16) = (320) / 4 = 80
Thus, the LCM(20, 16) = 80.
Visual Representation: Venn Diagram
A Venn diagram can visually represent the relationship between the multiples of 20 and 16, helping to understand the concept of LCM. Each circle represents the multiples of a number, and the overlapping area represents the common multiples. The smallest number in the overlapping area is the LCM. While drawing a complete Venn diagram for all multiples is impractical, it helps conceptually. Imagine the multiples of 20 in one circle and the multiples of 16 in another. 80 would be the smallest number present in both circles, illustrating the LCM.
Applications of LCM
The concept of LCM has wide-ranging applications in various fields:
-
Scheduling: Determining when events with different repeating cycles will occur simultaneously (e.g., two buses arriving at the same stop). If Bus A arrives every 20 minutes and Bus B every 16 minutes, they will both arrive together at the LCM(20, 16) = 80 minutes.
-
Fractions: Finding the least common denominator (LCD) when adding or subtracting fractions. The LCD is the LCM of the denominators.
-
Ratio and Proportion: Solving problems involving ratios and proportions often requires finding the LCM to maintain consistent units.
-
Modular Arithmetic: LCM plays a crucial role in solving problems related to modular arithmetic and congruences.
-
Music Theory: Understanding rhythmic patterns and harmonies.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors? If the numbers are relatively prime (their GCD is 1), their LCM is simply their product. For example, LCM(15, 8) = 15 x 8 = 120, because GCD(15, 8) = 1.
-
Q: Can I use a calculator to find the LCM? Many scientific calculators and online calculators have built-in functions to calculate the LCM.
-
Q: Which method is the best? The prime factorization method is generally the most efficient, particularly for larger numbers. However, the listing multiples method is easier to understand for beginners. The GCD method is also very efficient, especially if you already know the GCD.
-
Q: What is the difference between LCM and GCD? LCM is the smallest common multiple, while GCD is the greatest common divisor. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
-
Q: Can we find the LCM of more than two numbers? Yes, the methods (especially prime factorization) can be extended to find the LCM of more than two numbers. For instance, to find the LCM of 20, 16, and 12, you would find the prime factorization of each number and then take the highest power of each prime factor present.
Conclusion: Mastering the LCM
Understanding the least common multiple is a cornerstone of number theory with practical applications in various fields. This comprehensive guide explored three different methods for calculating the LCM, illustrating the process with the example of 20 and 16. Whether you choose prime factorization, listing multiples, or the GCD method, the fundamental principle remains the same: finding the smallest positive integer divisible by all the given numbers. By mastering these methods, you will be well-equipped to tackle more complex mathematical problems and appreciate the elegant simplicity of this fundamental concept. Remember to practice these methods regularly to solidify your understanding and improve your problem-solving skills. The ability to calculate the LCM efficiently is a valuable skill in mathematics and beyond.
Latest Posts
Latest Posts
-
Hypotenuse Of An Isosceles Triangle
Sep 17, 2025
-
Simplify Square Root Of 145
Sep 17, 2025
-
Composite Numbers 1 To 1000
Sep 17, 2025
-
Gcf Of 6 And 14
Sep 17, 2025
-
Parabola In Real Life Examples
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 20 And 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.