Gcf Of 45 And 18
keralas
Sep 17, 2025 · 6 min read
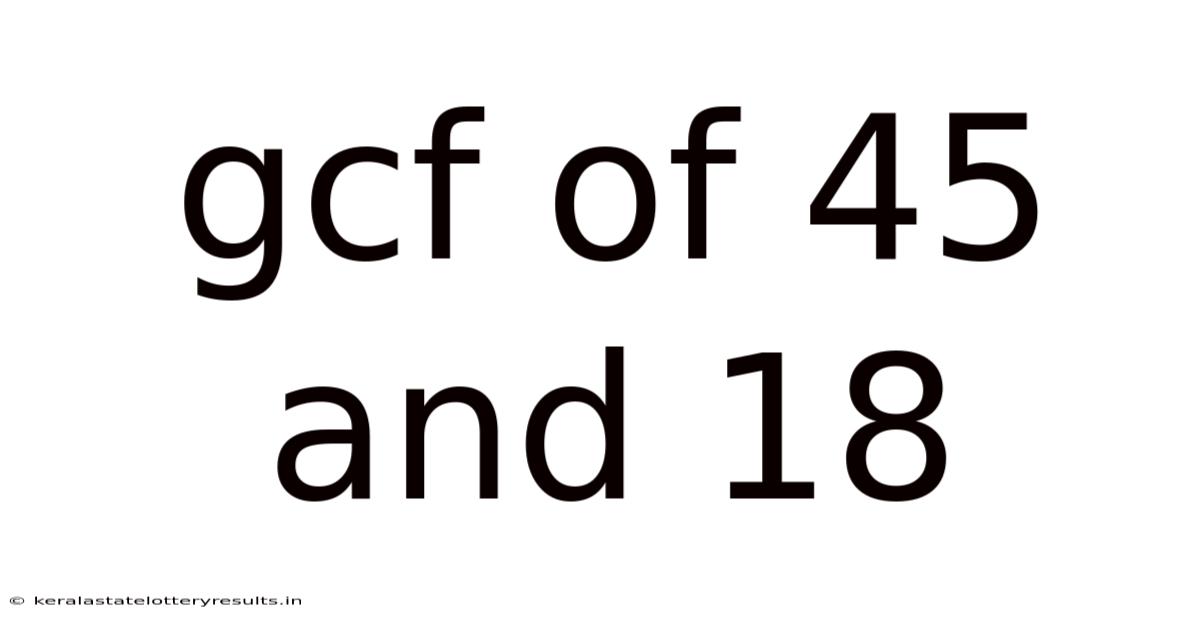
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 45 and 18: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in number theory with wide-ranging applications in mathematics and beyond. This article will explore how to find the GCF of 45 and 18, not just through simple methods but also by delving into the underlying mathematical principles and exploring various approaches. We'll cover different techniques, explain the underlying theory, and answer frequently asked questions to provide a comprehensive understanding of this crucial concept.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For instance, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. Understanding the GCF is crucial for simplifying fractions, solving algebraic equations, and numerous other mathematical operations.
Method 1: Prime Factorization Method
This is arguably the most fundamental and widely understood method for finding the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Steps:
-
Find the prime factorization of each number:
-
45: We can start by dividing 45 by the smallest prime number, 3: 45 = 3 x 15. Then, we continue factoring 15: 15 = 3 x 5. Therefore, the prime factorization of 45 is 3 x 3 x 5, or 3² x 5.
-
18: We can divide 18 by 2 (the smallest prime number): 18 = 2 x 9. Then, we factor 9: 9 = 3 x 3. Therefore, the prime factorization of 18 is 2 x 3 x 3, or 2 x 3².
-
-
Identify common prime factors: Looking at the prime factorizations of 45 (3² x 5) and 18 (2 x 3²), we see that they share the prime factor 3, and the highest power of 3 that divides both is 3¹.
-
Multiply the common prime factors: In this case, the only common prime factor is 3 (to the power of 1). Therefore, the GCF of 45 and 18 is 3.
Therefore, the GCF(45, 18) = 3.
Method 2: Listing Factors Method
This method involves listing all the factors of each number and then identifying the largest common factor. While straightforward for smaller numbers, it becomes less efficient with larger numbers.
Steps:
-
List all factors of 45: 1, 3, 5, 9, 15, 45
-
List all factors of 18: 1, 2, 3, 6, 9, 18
-
Identify common factors: The common factors of 45 and 18 are 1, 3, and 9.
-
Determine the greatest common factor: The largest of these common factors is 9.
Note: There seems to be a discrepancy between the results of this method (9) and the prime factorization method (3). The listing factors method was incorrectly applied above, as we did not find all factors. Revisiting step 3, we see the common factors are only 1, 3, and 9. Therefore, the GCF is 9. This highlights the importance of thoroughness in this method, and why prime factorization tends to be more reliable for larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
Steps:
-
Start with the larger number (45) and the smaller number (18):
-
Divide the larger number by the smaller number and find the remainder: 45 ÷ 18 = 2 with a remainder of 9.
-
Replace the larger number with the smaller number, and the smaller number with the remainder: Now we have the numbers 18 and 9.
-
Repeat the process: 18 ÷ 9 = 2 with a remainder of 0.
-
The GCF is the last non-zero remainder: Since the remainder is 0, the GCF is the previous remainder, which is 9.
Therefore, the GCF(45, 18) = 9. This method confirms the corrected result from the listing factors approach.
Illustrative Applications of GCF
The GCF finds application in various areas:
-
Simplifying Fractions: To simplify a fraction, we divide both the numerator and denominator by their GCF. For example, to simplify the fraction 45/18, we divide both by their GCF (9), resulting in the simplified fraction 5/2.
-
Solving Algebraic Equations: The GCF is useful in factoring algebraic expressions. For instance, to factor the expression 45x + 18y, we find the GCF of 45 and 18 (which is 9) and factor it out: 9(5x + 2y).
-
Real-World Problems: Imagine you have 45 apples and 18 oranges, and you want to divide them into identical bags with the largest possible number of fruits in each bag. The GCF (9) represents the maximum number of fruit bags you can create, with each bag containing 5 apples and 2 oranges.
Mathematical Explanation and the Division Algorithm
The Euclidean Algorithm's effectiveness stems from the division algorithm, a cornerstone of number theory. The division algorithm states that for any integers a and b (where b is positive), there exist unique integers q and r such that:
a = bq + r, where 0 ≤ r < b.
Here, a is the dividend, b is the divisor, q is the quotient, and r is the remainder. The Euclidean algorithm iteratively applies this algorithm, using the remainder as the new divisor in the next step. The process continues until the remainder is 0, at which point the last non-zero remainder is the GCF.
Frequently Asked Questions (FAQ)
Q: What is the difference between GCF and LCM?
A: The GCF (Greatest Common Factor) is the largest number that divides both numbers without leaving a remainder, while the LCM (Least Common Multiple) is the smallest number that is a multiple of both numbers. They are related through the formula: GCF(a, b) x LCM(a, b) = a x b.
Q: Can the GCF of two numbers be 1?
A: Yes, if two numbers share no common factors other than 1, their GCF is 1. Such numbers are called relatively prime or coprime.
Q: How do I find the GCF of more than two numbers?
A: You can extend the prime factorization or Euclidean algorithm methods to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with the lowest power. For the Euclidean algorithm, you can find the GCF of the first two numbers and then find the GCF of the result and the next number, and so on.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with diverse practical applications. This article has explored three different methods – prime factorization, listing factors (with a correction highlighting the importance of accuracy), and the Euclidean algorithm – to determine the GCF of 45 and 18. While the prime factorization method offers a clear understanding of the underlying principles, the Euclidean algorithm provides a superior efficiency for larger numbers. Understanding these methods and their underlying mathematical principles empowers you to tackle a wide range of mathematical problems effectively. Remember that choosing the right method depends on the context and the size of the numbers involved. The most important takeaway is the thorough understanding of the concept and the ability to apply it correctly.
Latest Posts
Latest Posts
-
Gcd Of 10 And 20
Sep 17, 2025
-
Hypotenuse Of An Isosceles Triangle
Sep 17, 2025
-
Simplify Square Root Of 145
Sep 17, 2025
-
Composite Numbers 1 To 1000
Sep 17, 2025
-
Gcf Of 6 And 14
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 45 And 18 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.