D Dx Of Log X
keralas
Sep 14, 2025 · 6 min read
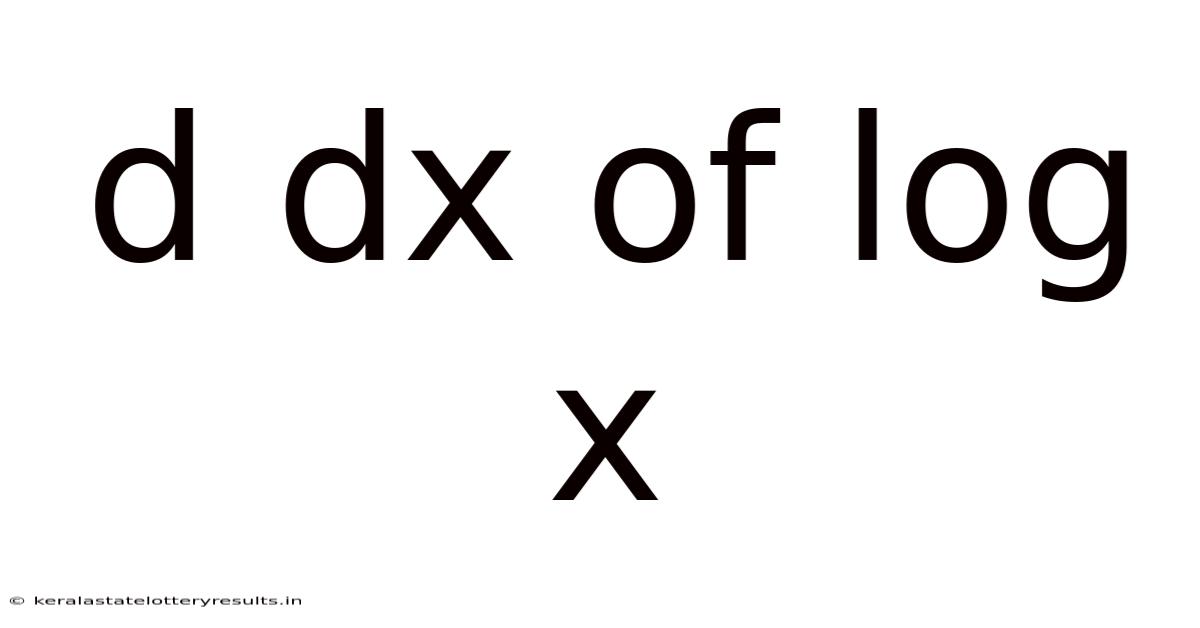
Table of Contents
Understanding d/dx of log x: A Comprehensive Guide
Finding the derivative of the logarithmic function, specifically d/dx of log x, is a fundamental concept in calculus. This seemingly simple problem underpins a wide range of applications in mathematics, physics, engineering, and economics. This comprehensive guide will delve into the intricacies of this derivative, explaining the process step-by-step, exploring its underlying principles, and addressing common questions. We will cover both the natural logarithm (ln x) and the logarithm with base 10 (log₁₀ x).
Introduction: The Power of Logarithms
Logarithms are the inverse functions of exponential functions. They are powerful tools for simplifying complex calculations, particularly those involving large numbers or exponents. Understanding their derivatives is crucial for anyone working with exponential growth or decay models, solving differential equations, or analyzing data with logarithmic scales. The derivative, d/dx, represents the instantaneous rate of change of a function with respect to x. Therefore, finding d/dx of log x helps us understand how quickly the logarithmic function changes at any given point.
1. Deriving d/dx of ln x (Natural Logarithm)
The natural logarithm, denoted as ln x, has a base of e, Euler's number (approximately 2.71828). Its derivative is remarkably simple and elegant. We'll derive it using the definition of the derivative and a key limit:
-
The Definition of the Derivative: The derivative of a function f(x) is defined as:
f'(x) = lim (h→0) [(f(x + h) - f(x)) / h]
-
Applying it to ln x: Let f(x) = ln x. Then:
f'(x) = lim (h→0) [(ln(x + h) - ln x) / h]
-
Using Logarithmic Properties: Recall that ln(a) - ln(b) = ln(a/b). Applying this:
f'(x) = lim (h→0) [ln((x + h) / x) / h]
-
Rewriting the Expression: We can rewrite (x + h) / x as 1 + (h/x):
f'(x) = lim (h→0) [ln(1 + (h/x)) / h]
-
A Crucial Limit: We use the important limit: lim (u→0) [ln(1 + u) / u] = 1. Let u = h/x. As h approaches 0, u also approaches 0. Therefore:
f'(x) = (1/x) * lim (u→0) [ln(1 + u) / u] = (1/x) * 1 = 1/x
Therefore, the derivative of ln x with respect to x is 1/x. This is a fundamental result in calculus.
2. Deriving d/dx of log₁₀ x (Logarithm Base 10)
The common logarithm, log₁₀ x, has a base of 10. To find its derivative, we use the change of base formula and the chain rule.
-
Change of Base Formula: logₐ b = (logₓ b) / (logₓ a). We can change the base of log₁₀ x to e:
log₁₀ x = ln x / ln 10
-
Applying the Chain Rule: The chain rule states that d/dx [f(g(x))] = f'(g(x)) * g'(x). Let f(u) = u/ln 10 and u = ln x. Then:
d/dx (log₁₀ x) = d/dx (ln x / ln 10) = (1/ln 10) * d/dx (ln x)
-
Substituting the Derivative of ln x: We already know that d/dx (ln x) = 1/x. Therefore:
d/dx (log₁₀ x) = (1/ln 10) * (1/x) = 1 / (x * ln 10)
Therefore, the derivative of log₁₀ x with respect to x is 1 / (x * ln 10).
3. Understanding the Results: Geometric Interpretation
The derivative 1/x for ln x tells us several important things:
- The rate of change decreases as x increases: The larger x becomes, the smaller the derivative becomes. This means the slope of the tangent line to the curve y = ln x gets shallower as x increases.
- The derivative is undefined at x = 0: The natural logarithm is undefined for x ≤ 0, reflecting the fact that you cannot take the logarithm of a non-positive number. This is consistent with the derivative being undefined at x = 0.
- The derivative is always positive for x > 0: This signifies that the natural logarithm function is strictly increasing for positive x values.
Similarly, the derivative 1 / (x * ln 10) for log₁₀ x shows a similar pattern, albeit scaled by the constant factor 1/ln 10. The rate of change is still inversely proportional to x, indicating a decreasing rate of change as x increases.
4. Applications of d/dx of log x
The derivatives of logarithmic functions have wide-ranging applications in numerous fields:
- Optimization Problems: In economics and engineering, finding the maximum or minimum values often involves taking derivatives. If a function involves logarithms, knowing their derivatives is crucial for solving these problems.
- Differential Equations: Many differential equations in physics and engineering involve logarithmic functions. Understanding their derivatives is essential for solving these equations.
- Data Analysis: Logarithmic scales are frequently used to represent data across a wide range of magnitudes (e.g., Richter scale for earthquakes). The derivative helps in analyzing the rate of change within such scales.
- Growth and Decay Models: Exponential growth and decay are often modeled using logarithmic functions. The derivative helps analyze the instantaneous growth or decay rate.
5. Frequently Asked Questions (FAQs)
-
Q: What is the difference between ln x and log x?
A: ln x denotes the natural logarithm (base e), while log x often refers to the common logarithm (base 10). However, it's essential to always check the context to confirm the base of the logarithm.
-
Q: Can I use the power rule for differentiating log x?
A: No, the power rule (d/dx (xⁿ) = nxⁿ⁻¹) doesn't directly apply to logarithmic functions. The derivative of log x requires different techniques, as shown in the derivations above.
-
Q: What is the derivative of log₂ x?
A: Using the change of base formula and the chain rule, similar to the derivation for log₁₀ x, we find that the derivative of log₂ x is 1 / (x * ln 2).
-
Q: What happens when x is negative?
A: The logarithm function (whether natural or base 10) is undefined for negative values of x. Therefore, the derivative is not defined for x < 0.
-
Q: What are some common mistakes to avoid?
A: A common mistake is incorrectly applying the power rule to logarithmic functions. Remember to use the appropriate techniques demonstrated in this article. Another mistake is forgetting to consider the base of the logarithm when finding its derivative.
6. Conclusion: Mastering the Derivative of log x
Understanding the derivative of the logarithmic function, whether natural or base 10, is a cornerstone of calculus and its applications. By mastering this concept, you'll be equipped to tackle complex problems in various fields. This guide has provided a comprehensive explanation, detailed derivations, and practical applications to enhance your understanding. Remember the key results: d/dx (ln x) = 1/x and d/dx (log₁₀ x) = 1 / (x * ln 10). With practice and a solid grasp of these fundamentals, you'll be well-prepared to apply these concepts effectively. Remember to always clarify the base of the logarithm to avoid confusion and ensure accurate calculations. The beauty of mathematics lies in its precision, and careful consideration of each step is essential for achieving mastery.
Latest Posts
Latest Posts
-
Gcf Of 35 And 45
Sep 14, 2025
-
10 Square Root Of 3
Sep 14, 2025
-
1 Quart How Many Pints
Sep 14, 2025
-
The Accompanying Frequency Polygon Represents
Sep 14, 2025
-
9 Times 9 Times 9
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about D Dx Of Log X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.