9 Times 9 Times 9
keralas
Sep 14, 2025 · 6 min read
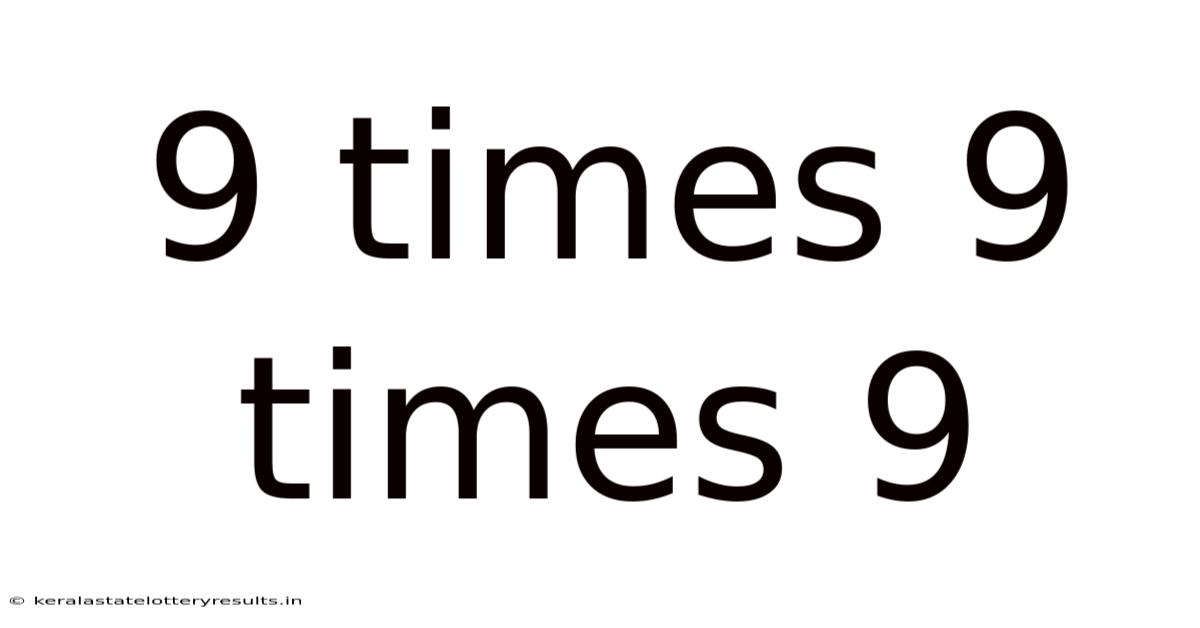
Table of Contents
Exploring the Mathematical Landscape of 9 x 9 x 9: Beyond Simple Multiplication
This article delves into the seemingly simple calculation of 9 x 9 x 9, exploring its mathematical underpinnings, its connections to other areas of mathematics, and its surprising applications in various fields. We'll move beyond the basic answer to uncover the richness and depth hidden within this seemingly straightforward problem. Understanding 9 x 9 x 9 offers a gateway to appreciating the interconnectedness of mathematical concepts and their practical relevance.
I. The Fundamental Calculation: 9 x 9 x 9 = 729
At its core, 9 x 9 x 9 is a straightforward multiplication problem. The calculation proceeds as follows:
- Step 1: 9 x 9 = 81 This is a fundamental multiplication fact that most students learn early in their mathematical education.
- Step 2: 81 x 9 = 729 This step can be performed using various methods, including long multiplication, mental math techniques (like breaking down 9 into 10 - 1), or using a calculator.
Therefore, the answer to 9 x 9 x 9 is definitively 729. This seemingly simple result, however, serves as a springboard for exploring more complex and fascinating mathematical ideas.
II. Exploring the Properties of 729
The number 729 itself possesses several interesting mathematical properties:
- Perfect Cube: 729 is a perfect cube, meaning it's the result of cubing an integer (9³ = 729). This connects our initial problem directly to the concept of exponents and powers.
- Sum of Consecutive Odd Numbers: 729 can be expressed as the sum of consecutive odd numbers: 1 + 3 + 5 + ... + 53 = 729. This illustrates a link between arithmetic series and cubic numbers.
- Divisibility: 729 is divisible by several numbers, including 1, 3, 9, 27, 81, and 729 itself. Exploring its divisors provides insights into number theory and prime factorization.
- Digital Root: The digital root of 729 (obtained by repeatedly summing its digits until a single digit remains) is 9 (7 + 2 + 9 = 18; 1 + 8 = 9). This highlights a connection to modular arithmetic and digit patterns.
Understanding these properties deepens our comprehension of 729 beyond its simple role as the result of 9 x 9 x 9.
III. Connections to Other Mathematical Concepts
The calculation 9 x 9 x 9 isn't isolated; it has connections to various areas of mathematics:
- Exponentiation: The problem directly utilizes exponentiation (9³). Understanding exponents is crucial in algebra, calculus, and numerous scientific applications.
- Number Theory: Investigating the properties of 729 leads to explorations in number theory, including prime factorization, divisibility rules, and the study of perfect cubes.
- Geometry: Cubes and cubic volumes are directly related to 9 x 9 x 9. Imagine a cube with side lengths of 9 units; its volume would be 729 cubic units. This demonstrates the practical application of cubic calculations in three-dimensional geometry.
- Algebra: The equation x³ = 729 has a simple solution (x = 9), illustrating the relationship between algebraic equations and numerical calculations. More complex cubic equations require more sophisticated algebraic techniques to solve.
- Combinatorics: In combinatorics, the number 729 could appear in various counting problems, potentially involving arrangements or selections of objects. The specific context would dictate the application.
IV. Applications in Real-World Scenarios
While seemingly abstract, the concept of 9 x 9 x 9, and more broadly, cubic calculations, finds applications in numerous real-world scenarios:
- Volume Calculations: Calculating the volume of cubes, rectangular prisms, or even approximating the volume of irregularly shaped objects often involves cubic calculations. This is essential in engineering, architecture, and various other fields.
- Data Storage: In computer science, data storage is often measured in units like kilobytes, megabytes, and gigabytes, which are based on powers of 2. However, understanding cubic calculations helps in visualizing and working with three-dimensional data structures.
- Physics and Engineering: Many physical phenomena, such as the volume of fluids, the displacement of objects, and calculations related to cubic crystals, rely on understanding and applying cubic calculations.
- Finance: Compound interest calculations, particularly over multiple periods, involve exponential growth, of which cubic calculations represent a specific case.
V. Expanding the Concept: Beyond 9 x 9 x 9
While we've focused on 9 x 9 x 9, it's beneficial to consider the broader implications:
- Other Cubes: Exploring the cubes of other numbers (e.g., 2³, 5³, 10³) helps build a broader understanding of exponentiation and cubic relationships.
- Higher Powers: Moving beyond cubes to higher powers (e.g., 9⁴, 9⁵) expands our understanding of exponential growth and its applications in various areas like compound interest and population modeling.
- Generalizing the Problem: We can generalize the problem to a³ for any integer 'a', allowing us to explore the properties of cubes in a more abstract mathematical context.
VI. Frequently Asked Questions (FAQ)
Q1: What are some real-world examples where I might use 9 x 9 x 9?
A1: Calculating the volume of a cube with 9-unit sides, determining the number of smaller cubes within a larger 9x9x9 cube, or even estimating the volume of a roughly cubical object.
Q2: Is there a quicker way to calculate 9 x 9 x 9 than using a calculator or manual multiplication?
A2: You can use mental math techniques. For example, recognizing that 9 x 9 = 81, and then multiplying 81 by 9 might be faster for some individuals. Breaking down 9 into (10-1) can be helpful for mental multiplication.
Q3: What are some other interesting mathematical properties of 729 besides being a perfect cube?
A3: 729 is the sum of consecutive odd numbers (1 + 3 + 5 +...+ 53), it's divisible by 1, 3, 9, 27, 81, and 729, and its digital root is 9.
Q4: How does 9 x 9 x 9 relate to geometry?
A4: It directly relates to the volume of a cube with sides of length 9 units. The result, 729, represents the number of cubic units that fill the cube.
VII. Conclusion: The Significance of Simple Calculations
The seemingly simple calculation of 9 x 9 x 9 provides a rich and rewarding exploration into various mathematical concepts. From its fundamental role in multiplication to its connections to exponents, number theory, geometry, and real-world applications, this problem underscores the interconnectedness of mathematics. By delving beyond the immediate answer of 729, we gain a deeper appreciation for the beauty and practical relevance of mathematics in everyday life and beyond. It serves as a reminder that even seemingly simple mathematical problems can unlock a world of deeper understanding and fascinating connections. The journey from 9 x 9 x 9 to an understanding of its implications is a testament to the power and elegance of mathematical exploration.
Latest Posts
Latest Posts
-
4 To The 8 Power
Sep 14, 2025
-
What Is Sin 45 Degree
Sep 14, 2025
-
Nine Tenths As A Decimal
Sep 14, 2025
-
Is 1681 A Prime Number
Sep 14, 2025
-
How Many Feet 1 4 Mile
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 9 Times 9 Times 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.