10 Square Root Of 3
keralas
Sep 14, 2025 · 5 min read
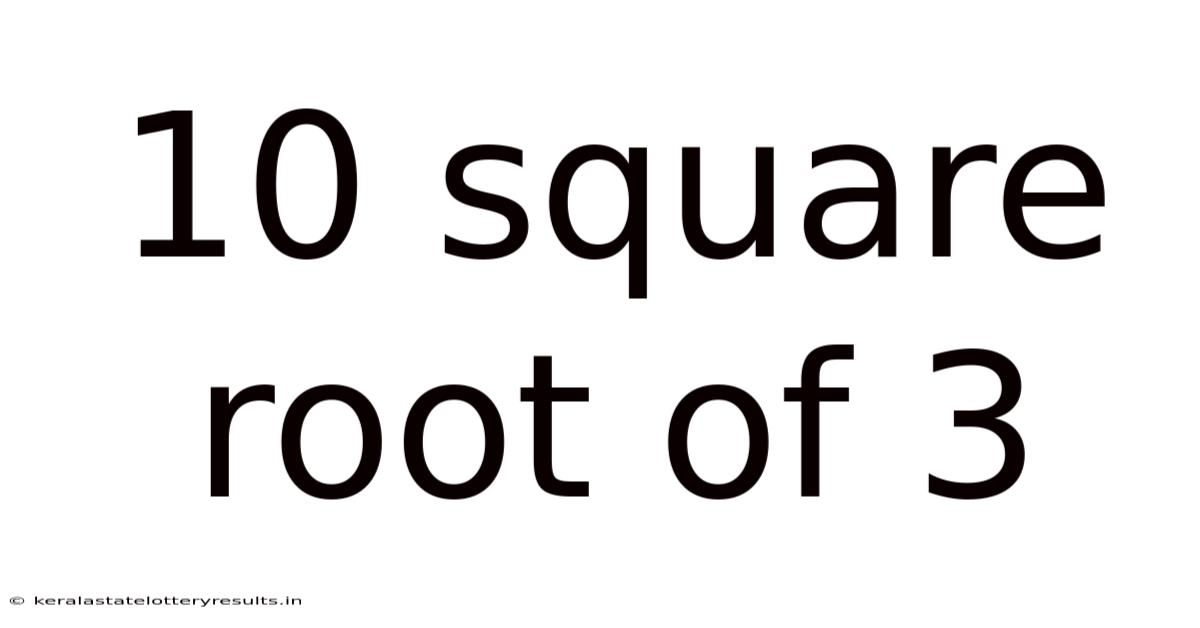
Table of Contents
Unveiling the Mysteries of 10√3: A Deep Dive into the World of Irrational Numbers
The expression "10√3" might seem intimidating at first glance, conjuring up images of complex mathematical equations and confusing formulas. However, understanding this seemingly simple expression unlocks a gateway to a deeper appreciation of irrational numbers, their properties, and their practical applications in various fields. This comprehensive guide will demystify 10√3, exploring its calculation, significance, and relevance in geometry, trigonometry, and beyond. We will also delve into the fascinating world of irrational numbers and their place within the broader mathematical landscape.
Understanding Irrational Numbers: Beyond the Rational
Before we delve into the specifics of 10√3, it's crucial to understand the nature of irrational numbers. Unlike rational numbers, which can be expressed as a fraction of two integers (e.g., 1/2, 3/4, -5/7), irrational numbers cannot be expressed as such. Their decimal representations are non-terminating and non-repeating, meaning they go on forever without ever settling into a predictable pattern. Famous examples include π (pi) and e (Euler's number), both fundamental constants in mathematics and physics.
√3 (the square root of 3) falls into this category. It represents the number which, when multiplied by itself, equals 3. Its decimal representation begins 1.7320508… and continues infinitely without any repeating sequence. This inherent "irrationality" might seem abstract, but it has profound implications across various fields.
Calculating 10√3: Methods and Approximations
Calculating 10√3 involves two steps: finding the approximate value of √3 and then multiplying it by 10. Several methods can be employed to achieve this:
1. Using a Calculator: The simplest approach is using a scientific calculator. Simply input "√3" and then multiply the result by 10. Most calculators will provide a high degree of accuracy, typically displaying several decimal places.
2. Using a Square Root Algorithm: For those interested in a more manual approach, various algorithms exist for approximating square roots. One common method is the Babylonian method (also known as Heron's method), an iterative process that refines an initial guess to progressively closer approximations. While this requires more steps, it offers a deeper understanding of how square roots are calculated.
3. Using a Taylor Series Expansion: For a more advanced approach, the Taylor series expansion can be used to approximate the value of √3. This involves representing the function as an infinite sum of terms, allowing for progressively more accurate approximations as more terms are included. This method is particularly useful in computer programming and advanced mathematical analysis.
Regardless of the method used, the result will always be an approximation, as √3 is irrational. The accuracy of the approximation depends on the chosen method and the number of decimal places considered. For most practical purposes, using a calculator provides sufficient accuracy. A common approximation is 17.32, which is accurate enough for many applications.
The Significance of 10√3 in Geometry and Trigonometry
The expression 10√3 frequently appears in geometry and trigonometry, particularly when dealing with equilateral triangles and 30-60-90 triangles.
Equilateral Triangles: In an equilateral triangle with side length 'a', the height (h) is given by the formula h = (a√3)/2. If the side length is 20 units, the height becomes 10√3 units. This illustrates the direct relationship between 10√3 and the dimensions of a specific equilateral triangle.
30-60-90 Triangles: These triangles are special right-angled triangles with angles of 30°, 60°, and 90°. The ratio of their sides is 1:√3:2. If the hypotenuse is 20 units, the side opposite the 60° angle will be 10√3 units. This showcases another geometric context where 10√3 arises naturally.
These geometric applications highlight the practical relevance of 10√3 in solving problems involving lengths, areas, and volumes of various shapes. Understanding this number's geometric significance simplifies calculations and enhances problem-solving skills.
Applications Beyond Geometry and Trigonometry
While geometry and trigonometry provide the most direct applications, 10√3, or more generally, multiples of √3, appear in other areas of mathematics and science:
-
Physics: Certain physical phenomena, particularly those involving vectors and forces, often involve calculations that result in expressions containing √3. Examples include calculations related to simple harmonic motion or the analysis of crystal structures.
-
Engineering: Engineering designs frequently utilize geometric principles, leading to the incorporation of √3 in calculations relating to structural integrity, material science, and mechanical design.
-
Computer Graphics: In computer graphics and game development, √3 often appears in calculations involving 3D transformations, rotations, and vector operations. Accurate representation of √3 is crucial for rendering realistic and accurate visuals.
Frequently Asked Questions (FAQ)
Q1: What is the exact value of 10√3?
A1: There is no exact decimal value for 10√3 because √3 is an irrational number. Any decimal representation will be an approximation.
Q2: How can I calculate 10√3 without a calculator?
A2: You can use approximation methods like the Babylonian method or Taylor series expansion, but these require more steps and may not provide high accuracy.
Q3: What are the practical applications of understanding 10√3?
A3: Understanding 10√3 is crucial for solving geometric problems involving equilateral and 30-60-90 triangles. It's also relevant in various fields like physics, engineering, and computer graphics where calculations involving irrational numbers are common.
Q4: Is 10√3 a rational or irrational number?
A4: 10√3 is an irrational number because it's the product of a rational number (10) and an irrational number (√3). The product of a rational and an irrational number is always irrational.
Q5: Can 10√3 be simplified further?
A5: No, 10√3 is already in its simplest form. 10 and √3 share no common factors other than 1.
Conclusion: Embracing the Irrational
10√3, while seemingly a simple mathematical expression, embodies the fascinating world of irrational numbers. Its presence in various geometric contexts and its relevance in numerous fields underscore the importance of understanding and appreciating irrational numbers beyond their seemingly abstract nature. While we can only approximate its decimal value, its precise mathematical representation holds significant weight in problem-solving and scientific exploration. Mastering the concepts related to 10√3 enhances mathematical proficiency and provides a stronger foundation for tackling more complex problems across diverse disciplines. The seemingly simple "10√3" thus represents a powerful gateway to a deeper understanding of mathematics and its profound impact on our world.
Latest Posts
Latest Posts
-
What Is Sin 45 Degree
Sep 14, 2025
-
Nine Tenths As A Decimal
Sep 14, 2025
-
Is 1681 A Prime Number
Sep 14, 2025
-
How Many Feet 1 4 Mile
Sep 14, 2025
-
How Long Is 72 Days
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 10 Square Root Of 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.