3/5 As An Equivalent Fraction
keralas
Sep 13, 2025 · 7 min read
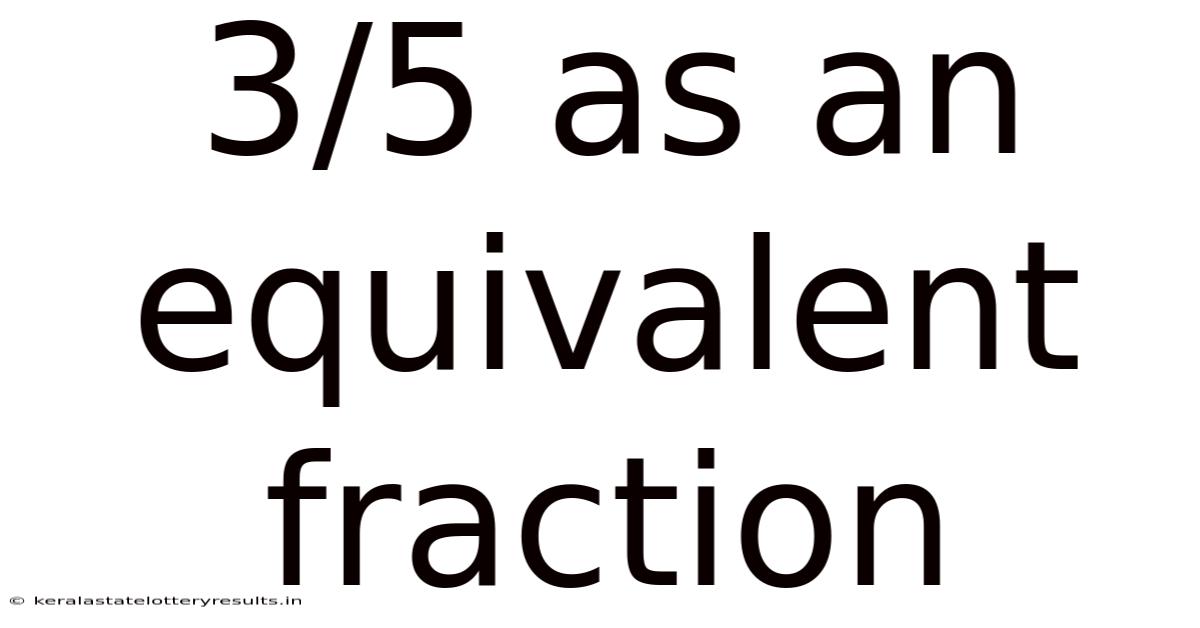
Table of Contents
Understanding 3/5: Exploring Equivalent Fractions and Their Applications
The fraction 3/5 represents three parts out of a total of five equal parts. Understanding this seemingly simple fraction opens the door to a world of mathematical concepts, including equivalent fractions, ratios, proportions, and even percentages. This comprehensive guide will delve into the intricacies of 3/5, exploring its equivalent fractions, demonstrating its practical applications, and answering frequently asked questions. Mastering this fundamental concept will significantly enhance your mathematical skills and problem-solving abilities.
Introduction to Fractions and Equivalent Fractions
A fraction, at its core, represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts, while the numerator shows how many of those parts are being considered.
Equivalent fractions are fractions that represent the same value, even though they look different. They are obtained by multiplying or dividing both the numerator and the denominator by the same non-zero number. This process doesn't change the fundamental ratio, just its representation. For example, 1/2 is equivalent to 2/4, 3/6, 4/8, and so on. All these fractions represent the same proportion – one-half.
Finding Equivalent Fractions for 3/5
Finding equivalent fractions for 3/5 involves multiplying both the numerator and the denominator by the same number. Let's explore some examples:
- Multiplying by 2: (3 x 2) / (5 x 2) = 6/10
- Multiplying by 3: (3 x 3) / (5 x 3) = 9/15
- Multiplying by 4: (3 x 4) / (5 x 4) = 12/20
- Multiplying by 5: (3 x 5) / (5 x 5) = 15/25
- Multiplying by 10: (3 x 10) / (5 x 10) = 30/50
As you can see, 6/10, 9/15, 12/20, 15/25, 30/50, and countless other fractions are equivalent to 3/5. They all represent the same proportion – three-fifths. The choice of which equivalent fraction to use often depends on the context of the problem. Sometimes, a simpler fraction is preferred (like 3/5 itself), while other times, a fraction with a larger denominator might be more useful for comparisons or calculations.
Simplifying Fractions: Finding the Simplest Form
While we can generate infinitely many equivalent fractions by multiplying, we can also simplify fractions by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
For 3/5, the GCD of 3 and 5 is 1. This means that 3/5 is already in its simplest form. We cannot simplify it further while maintaining its value. This is because 3 and 5 are coprime numbers; they share no common factors other than 1.
Representing 3/5 Visually
Visual representations can significantly enhance our understanding of fractions. Several ways to visualize 3/5 include:
- A circle divided into five equal slices: Shade three of the slices to represent 3/5.
- A rectangle divided into five equal columns: Shade three of the columns to represent 3/5.
- A number line: Mark five equally spaced points, labeling them 0, 1/5, 2/5, 3/5, 4/5, and 1. 3/5 would be the third mark from 0.
These visual aids help to solidify the concept of 3/5 as three parts out of a total of five equal parts. This concrete representation makes it easier to grasp the concept, especially for visual learners.
Practical Applications of 3/5
The fraction 3/5, and its equivalent fractions, pops up in numerous real-world scenarios. Here are a few examples:
- Cooking: A recipe calls for 3 cups of flour out of a total of 5 cups of dry ingredients. This is a 3/5 ratio.
- Shopping: A store offers a 3/5 discount on selected items. This means you pay only 2/5 of the original price.
- Surveys and Statistics: If 3 out of every 5 people surveyed prefer a particular brand, the preference rate is 3/5 or 60%.
- Geometry: Consider a rectangle divided into 5 equal squares. If 3 squares are shaded, the shaded area represents 3/5 of the total area.
- Probability: If there are 5 equally likely outcomes in an event, and 3 of them are favorable, the probability of a favorable outcome is 3/5.
These examples highlight the versatility of 3/5 and its equivalent fractions in representing proportions and ratios in various contexts.
Converting 3/5 to a Decimal and Percentage
Converting fractions to decimals and percentages is a crucial skill. To convert 3/5 to a decimal, we simply divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
Therefore, 3/5 is equal to 0.6.
To convert the decimal 0.6 to a percentage, we multiply by 100:
0.6 x 100 = 60%
So, 3/5 is equivalent to 60%.
Comparing Fractions: 3/5 and Other Fractions
Comparing fractions requires a common denominator. Let's compare 3/5 to other fractions:
- 3/5 vs. 1/2: To compare, find a common denominator (10). 3/5 becomes 6/10, and 1/2 becomes 5/10. Since 6/10 > 5/10, 3/5 > 1/2.
- 3/5 vs. 2/3: A common denominator is 15. 3/5 becomes 9/15, and 2/3 becomes 10/15. Since 9/15 < 10/15, 3/5 < 2/3.
This demonstrates the importance of finding common denominators for accurate fraction comparisons.
Adding and Subtracting Fractions with 3/5
Adding and subtracting fractions require a common denominator. Let's look at examples:
- 1/5 + 3/5 = (1+3)/5 = 4/5 (This is straightforward since they already share a denominator)
- 2/3 + 3/5: Find a common denominator (15). 2/3 becomes 10/15, and 3/5 becomes 9/15. 10/15 + 9/15 = 19/15, or 1 4/15.
- 1 - 3/5: Rewrite 1 as 5/5. 5/5 - 3/5 = 2/5.
Multiplying and Dividing Fractions with 3/5
Multiplying fractions is simpler than adding or subtracting. Multiply the numerators together and the denominators together:
- 3/5 x 2/3 = (3 x 2) / (5 x 3) = 6/15 = 2/5 (Remember to simplify if possible)
Dividing fractions involves inverting the second fraction (reciprocal) and then multiplying:
- 3/5 ÷ 2/3 = 3/5 x 3/2 = 9/10
Frequently Asked Questions (FAQ)
Q: What are some real-world examples where 3/5 is used?
A: 3/5 is used extensively in various fields, including cooking (measuring ingredients), finance (representing proportions of investments), statistics (representing percentages), and probability (calculating chances of events).
Q: How do I explain 3/5 to a child?
A: Use visual aids like a pizza cut into five slices. Explain that if you eat three slices, you've eaten 3/5 of the pizza.
Q: Is there an easier way to find equivalent fractions of 3/5?
A: The simplest way is to multiply both the numerator and the denominator by the same whole number.
Q: Can 3/5 be expressed as a mixed number?
A: No, 3/5 is a proper fraction (numerator is less than the denominator), so it cannot be expressed as a mixed number (a whole number and a proper fraction).
Q: How can I convert 3/5 to a percentage without using a calculator?
A: Convert 3/5 to a decimal (0.6) by dividing 3 by 5, then multiply the decimal by 100 to get the percentage (60%).
Conclusion
Understanding the fraction 3/5 and its equivalent fractions is a cornerstone of fundamental mathematics. This comprehensive exploration has covered various aspects, from finding equivalent fractions and simplifying to visualizing, applying, and comparing them. Mastering these concepts will significantly improve your mathematical proficiency and problem-solving skills, empowering you to confidently tackle more complex mathematical challenges. Remember that practice is key – the more you work with fractions, the more intuitive and comfortable you will become.
Latest Posts
Latest Posts
-
What Is 73 Divisible By
Sep 13, 2025
-
Gcf Of 7 And 21
Sep 13, 2025
-
X C V I I
Sep 13, 2025
-
Consecutive Odd And Even Numbers
Sep 13, 2025
-
One Thousand And Three Hundred
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3/5 As An Equivalent Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.