Gcf Of 7 And 21
keralas
Sep 13, 2025 · 6 min read
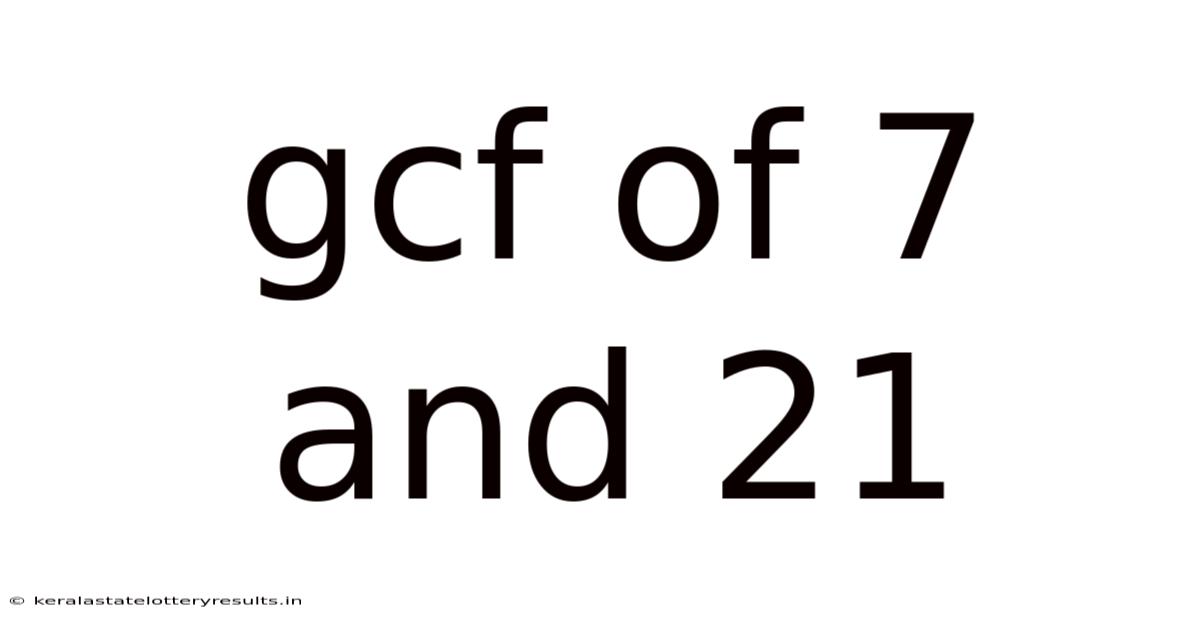
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 7 and 21: A Deep Dive into Number Theory
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying principles behind calculating the GCF of numbers like 7 and 21 unlocks a deeper appreciation of number theory and its applications in various fields, from cryptography to computer science. This article will not only explain how to find the GCF of 7 and 21 but also explore different methods, delve into the mathematical concepts involved, and provide a broader perspective on the significance of GCF in mathematics.
Understanding the Concept of Greatest Common Factor (GCF)
The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6; therefore, the GCF of 12 and 18 is 6.
Our focus here is on finding the GCF of 7 and 21. This seemingly simple problem provides a perfect illustration of the core concepts and techniques used to determine the GCF of any two numbers.
Method 1: Listing Factors
The most straightforward method, particularly for smaller numbers like 7 and 21, involves listing all the factors of each number and identifying the largest common factor.
Factors of 7: 1, 7 Factors of 21: 1, 3, 7, 21
By comparing the lists, we see that the common factors of 7 and 21 are 1 and 7. The greatest of these common factors is 7. Therefore, the GCF(7, 21) = 7.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works well for larger numbers. It involves expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 7: 7 (7 is a prime number itself)
- Prime factorization of 21: 3 x 7
Once we have the prime factorizations, we identify the common prime factors and their lowest powers. In this case, the only common prime factor is 7, and its lowest power is 7¹. Therefore, the GCF(7, 21) = 7.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal.
Let's apply the Euclidean algorithm to find the GCF(7, 21):
- Divide the larger number (21) by the smaller number (7): 21 ÷ 7 = 3 with a remainder of 0.
Since the remainder is 0, the smaller number (7) is the GCF. Therefore, GCF(7, 21) = 7.
Explanation of the Euclidean Algorithm: A Deeper Dive
The Euclidean algorithm relies on the following property: If a and b are two integers, and a > b, then GCF(a, b) = GCF(b, a mod b), where a mod b is the remainder when a is divided by b.
Let's break down why this works. Consider two numbers, a and b, where a > b. We can express a as a multiple of b plus a remainder:
a = q b + r, where q is the quotient and r is the remainder (0 ≤ r < b).
Any common divisor of a and b must also divide r (since it divides a and q b). Conversely, any common divisor of b and r must also divide a (since it divides b and q b + r). Therefore, the set of common divisors of a and b is the same as the set of common divisors of b and r. This means that GCF(a, b) = GCF(b, r). We repeat this process until the remainder is 0, at which point the GCF is the last non-zero remainder.
The Euclidean algorithm's efficiency stems from its iterative nature; it reduces the problem to smaller and smaller numbers, quickly converging on the GCF. This makes it computationally far superior to methods like prime factorization for very large numbers.
Applications of GCF
The concept of the greatest common factor is far from a mere academic exercise. It finds practical applications in numerous areas:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. To simplify a fraction, we divide both the numerator and the denominator by their GCF.
-
Solving Diophantine Equations: Diophantine equations are algebraic equations where only integer solutions are sought. The GCF plays a critical role in determining the solvability of certain types of Diophantine equations.
-
Cryptography: GCF is fundamental in various cryptographic algorithms, particularly in RSA encryption, a widely used public-key cryptosystem. The security of RSA relies on the difficulty of factoring large numbers into their prime factors—a problem closely related to finding the GCF.
-
Computer Science: The Euclidean algorithm, used to find the GCF, is an efficient algorithm used in various computer science applications, including modular arithmetic and cryptography.
Frequently Asked Questions (FAQ)
-
Q: What if the GCF of two numbers is 1?
- A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
-
Q: Can I find the GCF of more than two numbers?
- A: Yes, you can extend the methods discussed above to find the GCF of more than two numbers. For the Euclidean algorithm, you would repeatedly apply the algorithm to pairs of numbers.
-
Q: Is there a formula for calculating the GCF?
- A: There isn't a single, direct formula for calculating the GCF for all pairs of numbers. However, the methods described (listing factors, prime factorization, and the Euclidean algorithm) provide systematic ways to determine it.
-
Q: Why is the Euclidean algorithm more efficient for large numbers?
- A: The Euclidean algorithm's efficiency lies in its iterative reduction of the problem size. It avoids the potentially computationally expensive process of finding all factors or prime factors for very large numbers.
Conclusion
Finding the greatest common factor of 7 and 21, while seemingly trivial, provides a valuable gateway to understanding fundamental concepts in number theory. The methods outlined—listing factors, prime factorization, and the Euclidean algorithm—offer different approaches, each with its own strengths and applications. Understanding these methods not only enhances mathematical proficiency but also highlights the practical importance of GCF in various fields, showcasing its relevance beyond simple arithmetic. The simplicity of the GCF(7,21) = 7 belies the profound mathematical principles underpinning its calculation and the wide-ranging applications of this seemingly simple concept. From simplifying fractions to securing cryptographic systems, the GCF continues to be a cornerstone of mathematical understanding and practical application.
Latest Posts
Latest Posts
-
Gcf Of 96 And 84
Sep 13, 2025
-
Gcf Of 15 And 24
Sep 13, 2025
-
What Times What Equals 112
Sep 13, 2025
-
What Is 34 C In Farenhuit
Sep 13, 2025
-
Compare Fractions With Different Denominators
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 7 And 21 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.