What Is 20 Of 80.00
keralas
Sep 16, 2025 · 6 min read
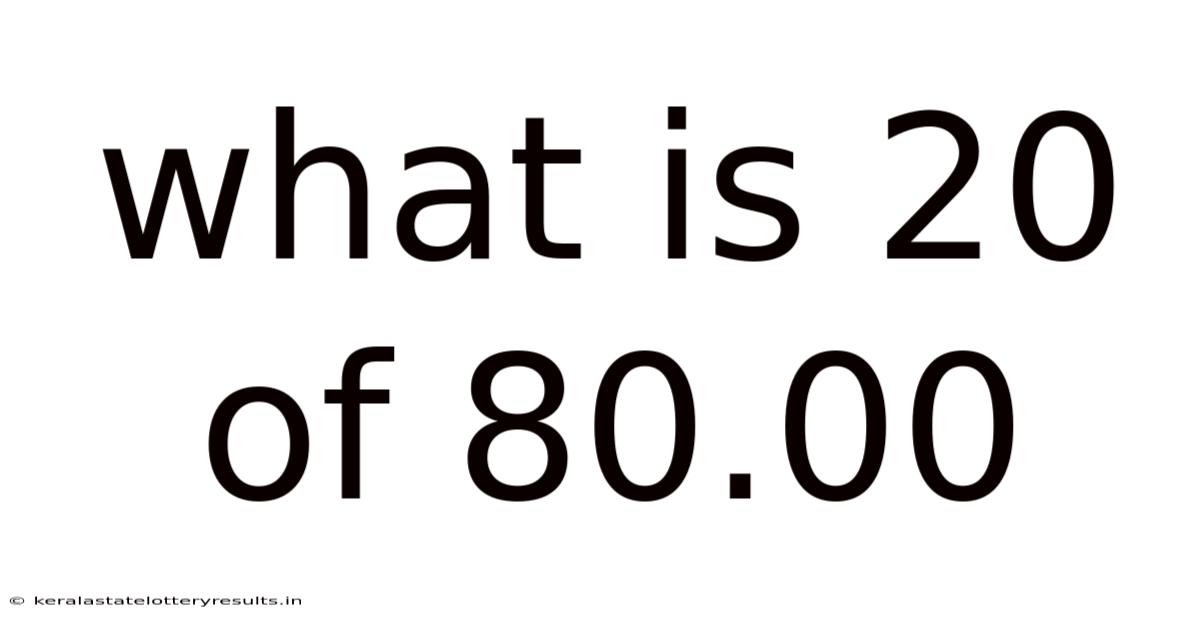
Table of Contents
What is 20% of 80.00? A Deep Dive into Percentages and Their Applications
This article will explore the seemingly simple question: "What is 20% of 80.00?" We'll delve into the fundamental concept of percentages, demonstrate multiple ways to calculate this specific problem, and then broaden the discussion to explore the practical applications of percentage calculations in various fields. Understanding percentages is a crucial skill in everyday life, from budgeting and shopping to analyzing data and understanding financial reports. This comprehensive guide will equip you with the knowledge and tools to confidently tackle any percentage-related problem.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (from Latin "per centum"). Therefore, 20% can be written as 20/100 or 0.20 (as a decimal). This representation is fundamental to understanding how percentages work.
When we ask "What is 20% of 80.00?", we are essentially asking: "What is 20/100 * 80.00?". This phrase translates directly into a mathematical equation that we can solve.
Method 1: Using the Decimal Equivalent
The most straightforward method is to convert the percentage to its decimal equivalent and then multiply it by the number.
- Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Multiply the decimal by the number: 0.20 * 80.00 = 16.00
Therefore, 20% of 80.00 is 16.00.
Method 2: Using Fractions
We can also solve this using fractions.
- Express the percentage as a fraction: 20% = 20/100
- Simplify the fraction (if possible): 20/100 simplifies to 1/5
- Multiply the fraction by the number: (1/5) * 80.00 = 80.00 / 5 = 16.00
Again, we arrive at the answer: 20% of 80.00 is 16.00.
Method 3: Using Proportion
This method is particularly useful for understanding the underlying relationship between percentages and the whole. We can set up a proportion:
20/100 = x/80
Where 'x' represents the unknown value (20% of 80.00). To solve for x, we cross-multiply:
20 * 80 = 100 * x 1600 = 100x x = 1600/100 x = 16
Therefore, 20% of 80.00 is 16.00.
Beyond the Calculation: Real-World Applications
The ability to calculate percentages has far-reaching applications across numerous fields:
-
Finance: Calculating interest on loans, determining discounts, understanding tax rates, analyzing investment returns, and calculating profit margins all rely heavily on percentage calculations. For example, a 5% interest rate on a loan of $10,000 means you’ll pay $500 in interest.
-
Retail and Sales: Calculating discounts (e.g., a 25% off sale), determining sales tax, and comparing prices are all common uses of percentages in retail settings. Understanding markups and margins is also crucial for businesses.
-
Science and Statistics: Percentages are used extensively in scientific research to express data and probabilities. For example, expressing the percentage of a population with a certain characteristic or the success rate of an experiment. Statistical significance is often expressed as a percentage.
-
Data Analysis: Percentages are crucial for interpreting data, comparing different data sets, and visualizing trends. For instance, visualizing the percentage change in sales over time or comparing the market share of competing companies.
-
Everyday Life: From tipping in restaurants (15-20% is common) to understanding nutritional information (e.g., the percentage of daily value of vitamins in food), percentages are integrated into our daily lives. Budgeting and saving often involves setting aside a certain percentage of income.
-
Education: Grasping percentage concepts is fundamental to understanding many subjects, from mathematics and statistics to economics and science. Analyzing test scores and calculating grades often involves working with percentages.
Advanced Percentage Calculations: Beyond the Basics
While calculating 20% of 80.00 is relatively straightforward, let's explore more complex scenarios:
-
Calculating the Percentage Increase or Decrease: This involves determining the percentage change between two numbers. The formula is: [(New Value - Old Value) / Old Value] * 100%. For instance, if your salary increases from $50,000 to $60,000, the percentage increase is [(60000 - 50000) / 50000] * 100% = 20%.
-
Finding the Original Value: If you know the percentage and the resulting value, you can work backward to find the original value. For example, if 15% of a number is 30, you can set up the equation: 0.15x = 30. Solving for x gives you the original value (x = 200).
-
Compound Interest: This is a more complex calculation involving interest accumulating on both the principal amount and the previously accumulated interest. The formula is A = P (1 + r/n)^(nt), where: A = the future value of the investment/loan, including interest; P = the principal investment amount (the initial deposit or loan amount); r = the annual interest rate (decimal); n = the number of times that interest is compounded per year; and t = the number of years the money is invested or borrowed for.
Frequently Asked Questions (FAQs)
-
Q: What are some common mistakes people make when working with percentages?
- A: A common mistake is incorrectly converting percentages to decimals. Remember to divide by 100. Another mistake is misinterpreting percentage increases or decreases. Always carefully consider whether the percentage is based on the original value or the new value. Finally, rounding errors can lead to inaccuracies, especially in complex calculations.
-
Q: How can I improve my understanding of percentages?
- A: Practice is key. Solve various percentage problems, starting with simple ones and gradually increasing the complexity. Use different methods to solve the same problem to reinforce your understanding. Online resources, textbooks, and practice exercises can help.
-
Q: Are there any online tools or calculators that can help with percentage calculations?
- A: Yes, many online percentage calculators are available. These can be helpful for quick calculations or for checking your work. However, it's essential to understand the underlying principles of percentage calculations to use these tools effectively.
-
Q: Why are percentages so important in everyday life?
- A: Percentages provide a standardized and easily understandable way to represent proportions and changes. This makes them valuable tools for comparing different quantities, analyzing data, and making informed decisions in various contexts, from personal finance to scientific research.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental skill applicable across many aspects of life. This article has provided a comprehensive guide to calculating percentages, starting with the simple example of finding 20% of 80.00 and expanding into more complex applications. By mastering percentage calculations, you will be better equipped to navigate financial decisions, analyze data effectively, and improve your understanding of the world around you. Remember, consistent practice and a firm grasp of the underlying principles will lead to confidence and proficiency in this essential mathematical concept. The ability to accurately and efficiently work with percentages is a valuable asset that will serve you well throughout your life.
Latest Posts
Latest Posts
-
What Is 60 Of 50
Sep 16, 2025
-
What Time Is 15 13
Sep 16, 2025
-
3 10 Of An Inch
Sep 16, 2025
-
What Is 1 3 2
Sep 16, 2025
-
What Is Half Of 12
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 80.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.