X2 5x 6 X 2
keralas
Sep 14, 2025 · 6 min read
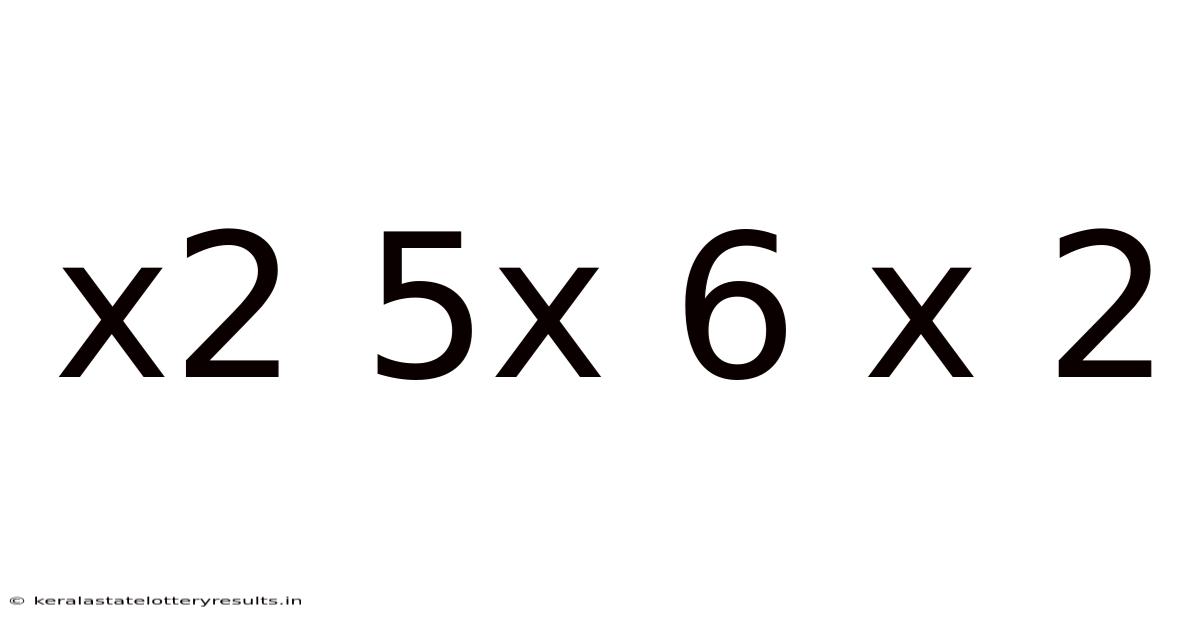
Table of Contents
Decoding the Mathematical Expression: x² + 5x + 6 = 0
This article delves into the intricacies of solving the quadratic equation x² + 5x + 6 = 0. We'll explore various methods to find the solutions (also known as roots or zeros), providing a comprehensive understanding suitable for students of various mathematical backgrounds. From basic factorization to the quadratic formula and graphical representations, we'll uncover the secrets behind this seemingly simple yet profoundly important equation. Understanding quadratic equations forms a crucial foundation in algebra and has wide-ranging applications in various fields, including physics, engineering, and economics.
Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero (otherwise, it wouldn't be a quadratic equation). In our specific case, we have a = 1, b = 5, and c = 6.
The solutions to a quadratic equation represent the x-values where the corresponding quadratic function (y = ax² + bx + c) intersects the x-axis (where y = 0). These solutions can be real numbers, complex numbers, or a combination of both, depending on the values of a, b, and c.
Method 1: Factorization
Factorization is the most straightforward method for solving quadratic equations, especially when the equation is easily factorable. The goal is to rewrite the quadratic expression as a product of two linear expressions. For x² + 5x + 6 = 0, we look for two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term). These numbers are 2 and 3.
Therefore, we can factor the equation as follows:
(x + 2)(x + 3) = 0
This equation is satisfied if either (x + 2) = 0 or (x + 3) = 0. Solving these linear equations gives us the solutions:
x + 2 = 0 => x = -2 x + 3 = 0 => x = -3
Thus, the solutions to the quadratic equation x² + 5x + 6 = 0 are x = -2 and x = -3.
Method 2: Quadratic Formula
The quadratic formula provides a general solution for any quadratic equation, regardless of its factorability. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our equation (a = 1, b = 5, c = 6), we get:
x = [-5 ± √(5² - 4 * 1 * 6)] / (2 * 1) x = [-5 ± √(25 - 24)] / 2 x = [-5 ± √1] / 2 x = (-5 ± 1) / 2
This gives us two solutions:
x = (-5 + 1) / 2 = -4 / 2 = -2 x = (-5 - 1) / 2 = -6 / 2 = -3
Again, we arrive at the solutions x = -2 and x = -3. The quadratic formula is particularly useful when factorization is difficult or impossible.
Method 3: Completing the Square
Completing the square is another algebraic method to solve quadratic equations. This method involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Let's apply this method to our equation:
x² + 5x + 6 = 0
- Move the constant term to the right side:
x² + 5x = -6
- Take half of the coefficient of x (5/2), square it ((5/2)² = 25/4), and add it to both sides:
x² + 5x + 25/4 = -6 + 25/4
- Factor the left side as a perfect square:
(x + 5/2)² = -6 + 25/4 = 1/4
- Take the square root of both sides:
x + 5/2 = ±√(1/4) = ±1/2
- Solve for x:
x = -5/2 ± 1/2
This gives us the two solutions:
x = -5/2 + 1/2 = -4/2 = -2 x = -5/2 - 1/2 = -6/2 = -3
Graphical Representation
The solutions of a quadratic equation can also be visualized graphically. The graph of the quadratic function y = x² + 5x + 6 is a parabola. The x-intercepts of this parabola represent the solutions to the equation x² + 5x + 6 = 0. In this case, the parabola intersects the x-axis at x = -2 and x = -3, confirming our solutions obtained algebraically.
The Discriminant: Understanding the Nature of Roots
The expression inside the square root in the quadratic formula (b² - 4ac) is called the discriminant. It provides valuable information about the nature of the roots:
- b² - 4ac > 0: The equation has two distinct real roots.
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex roots (conjugate pairs).
In our equation, x² + 5x + 6 = 0, the discriminant is:
5² - 4 * 1 * 6 = 25 - 24 = 1
Since the discriminant is positive (1 > 0), we confirmed that the equation has two distinct real roots, which are -2 and -3.
Applications of Quadratic Equations
Quadratic equations have numerous applications across diverse fields. Some examples include:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing structures, analyzing stresses and strains in materials.
- Economics: Modeling supply and demand curves, optimizing production levels.
- Computer graphics: Creating curves and shapes.
Frequently Asked Questions (FAQs)
Q1: What does it mean to "solve" a quadratic equation?
A1: Solving a quadratic equation means finding the values of the variable (x) that make the equation true (i.e., make the left-hand side equal to zero). These values are called the roots, solutions, or zeros of the equation.
Q2: Can a quadratic equation have only one solution?
A2: Yes, a quadratic equation can have only one solution if the discriminant (b² - 4ac) is equal to zero. This single solution is a repeated root.
Q3: Can a quadratic equation have no real solutions?
A3: Yes, if the discriminant (b² - 4ac) is negative, the equation has no real solutions. The solutions will be complex numbers involving the imaginary unit i (where i² = -1).
Q4: Why is the quadratic formula important?
A4: The quadratic formula provides a universal method for solving any quadratic equation, even those that are difficult or impossible to factor.
Q5: How can I check if my solutions are correct?
A5: Substitute your solutions back into the original equation. If both sides of the equation are equal, your solutions are correct.
Conclusion
Solving the quadratic equation x² + 5x + 6 = 0 demonstrates the fundamental principles of algebra and provides a stepping stone towards understanding more complex mathematical concepts. We explored three different methods – factorization, the quadratic formula, and completing the square – highlighting their strengths and applications. Understanding the discriminant allows us to predict the nature of the roots, providing further insight into the equation's behavior. The applications of quadratic equations are vast, making their mastery an essential skill for students in various disciplines. This comprehensive guide offers a strong foundation for tackling more challenging quadratic equations and related mathematical problems.
Latest Posts
Latest Posts
-
What Are Factors For 32
Sep 14, 2025
-
What Is Half Of 4 3
Sep 14, 2025
-
Is 617 A Prime Number
Sep 14, 2025
-
529 Is A Prime Number
Sep 14, 2025
-
Rotate About The Y Axis
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X2 5x 6 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.