What Is Half Of 4/3
keralas
Sep 14, 2025 · 6 min read
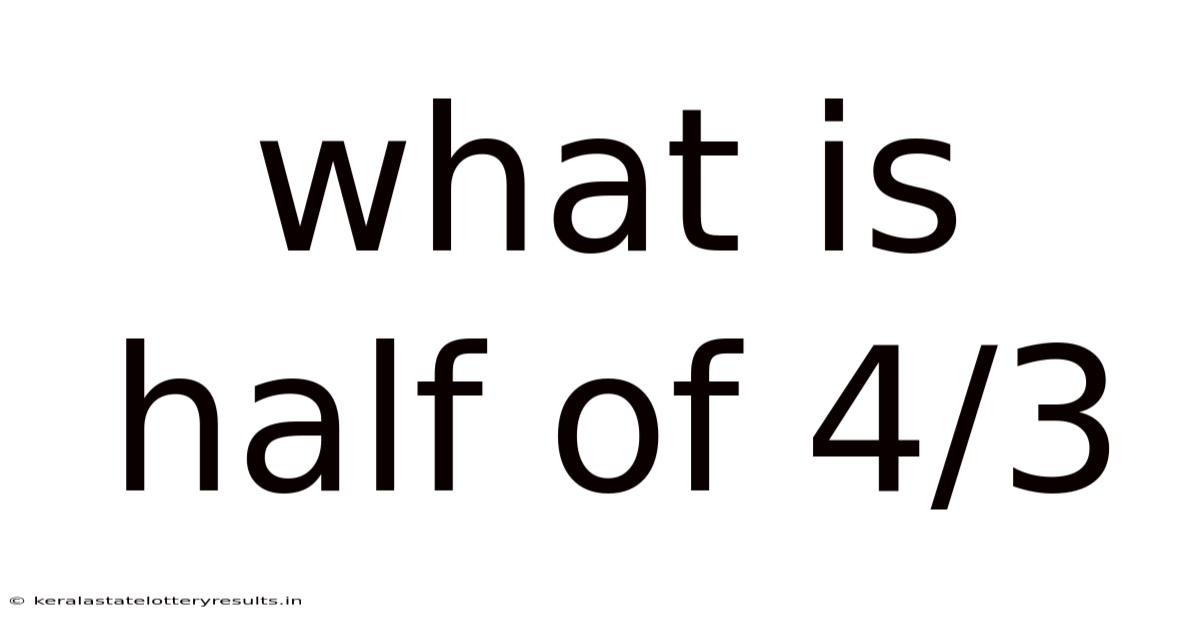
Table of Contents
What is Half of 4/3? A Deep Dive into Fractions and Division
Finding half of 4/3 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper understanding of fractions, division, and the fundamental principles of mathematics. This article will not only solve the problem but also explore the underlying concepts, providing a comprehensive guide for learners of all levels. We'll cover various methods of solving the problem, delve into the mathematical reasoning behind each step, and address frequently asked questions. By the end, you'll not only know the answer but also possess a stronger grasp of fractional arithmetic.
Understanding Fractions: The Building Blocks
Before tackling the problem of finding half of 4/3, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 4/3, the numerator is 4 and the denominator is 3. This means we have 4 parts of a whole that has been divided into 3 equal parts. Note that this is an improper fraction because the numerator is larger than the denominator – representing more than one whole.
Method 1: Direct Division
The most straightforward method to find half of 4/3 is to divide the fraction by 2. Remember, dividing by 2 is the same as multiplying by its reciprocal, which is 1/2. So, the calculation becomes:
(4/3) ÷ 2 = (4/3) × (1/2)
To multiply fractions, we simply multiply the numerators together and the denominators together:
(4 × 1) / (3 × 2) = 4/6
Now, we simplify the fraction by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD of 4 and 6 is 2. Dividing both the numerator and the denominator by 2 gives us:
4/6 = 2/3
Therefore, half of 4/3 is 2/3.
Method 2: Converting to a Mixed Number
Another approach involves converting the improper fraction 4/3 into a mixed number before dividing by 2. A mixed number consists of a whole number and a proper fraction. To convert 4/3 into a mixed number, we divide the numerator (4) by the denominator (3):
4 ÷ 3 = 1 with a remainder of 1
This means 4/3 is equivalent to 1 and 1/3 (or 1 1/3). Now, we find half of this mixed number:
(1 1/3) ÷ 2
This can be challenging to visualize directly. Let's convert the mixed number back into an improper fraction:
1 1/3 = (1 × 3 + 1) / 3 = 4/3
Now, we can use the same method as in Method 1:
(4/3) ÷ 2 = (4/3) × (1/2) = 4/6 = 2/3
Again, we arrive at the answer: 2/3.
Method 3: Visual Representation
While the above methods are mathematically precise, visualizing the problem can enhance understanding, especially for those who are visual learners. Imagine a pizza cut into three equal slices. 4/3 of a pizza would mean you have four of these slices – one whole pizza and one extra slice. To find half of this, you would simply divide the four slices in half, resulting in two slices. Since the whole pizza was divided into three slices, these two slices represent 2/3 of the whole pizza.
The Importance of Simplification
In both methods above, we simplified the fraction 4/6 to 2/3. Simplification is a crucial step in working with fractions. It reduces the fraction to its simplest form, making it easier to understand and compare with other fractions. A simplified fraction is equivalent to the original fraction but is expressed using smaller numbers.
Understanding Improper Fractions and Mixed Numbers
The problem highlights the importance of understanding improper fractions and mixed numbers. An improper fraction has a numerator greater than or equal to its denominator (e.g., 4/3, 5/2). A mixed number combines a whole number and a proper fraction (e.g., 1 1/3, 2 1/2). The ability to convert between these forms is essential for efficient fraction manipulation.
Beyond the Basics: Applications in Real Life
While this might seem like a purely theoretical exercise, understanding fraction manipulation has practical applications in numerous real-world scenarios. Consider these examples:
- Cooking and Baking: Recipes often require fractional amounts of ingredients. Calculating half a recipe necessitates understanding fraction division.
- Construction and Engineering: Precise measurements are critical, and fractions are used extensively to represent dimensions and quantities.
- Finance and Budgeting: Understanding fractions helps in managing finances, calculating percentages, and interpreting financial data.
- Science and Data Analysis: Fractions are fundamental in scientific calculations and data interpretation.
Frequently Asked Questions (FAQs)
Q: Can I divide the numerator and denominator separately by 2?
A: No, this is incorrect. Dividing the numerator and denominator by the same number is equivalent to simplifying the fraction, not dividing the entire fraction by 2. You need to multiply by 1/2, as explained in the methods above.
Q: What if the fraction wasn't 4/3, but a different improper fraction?
A: The same principles apply. You would still convert to a mixed number (if desired) and then multiply by 1/2.
Q: What if I needed a third of 4/3, or another fraction of it?
A: You'd replace 1/2 with the desired fraction and follow the same multiplication process. For example, to find a third of 4/3, you would calculate (4/3) × (1/3) = 4/9.
Q: Why is simplification important?
A: Simplification reduces the complexity of fractions, making them easier to work with and understand. It also ensures that the fraction is expressed in its most concise and accurate form.
Conclusion: Mastering Fractions, One Step at a Time
Finding half of 4/3, while seemingly trivial, provides a valuable opportunity to reinforce our understanding of fractions, division, and the interconnectedness of mathematical concepts. By exploring different solution methods and delving into the underlying principles, we've not only solved the problem but also gained a deeper appreciation for the power and practical applications of fractional arithmetic. Remember that consistent practice and a conceptual understanding are key to mastering these fundamental mathematical tools. With continued effort, you will build a strong foundation for more advanced mathematical concepts. So, embrace the challenge, practice regularly, and watch your mathematical skills blossom!
Latest Posts
Latest Posts
-
How Much Is 100 Mm
Sep 14, 2025
-
What Is 15 Of 15
Sep 14, 2025
-
Cuantos Centimetros Son 7 Pulgadas
Sep 14, 2025
-
Is 18 A Perfect Square
Sep 14, 2025
-
3 To The Power 7
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 4/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.