X Multiplied By X Equals
keralas
Sep 15, 2025 · 6 min read
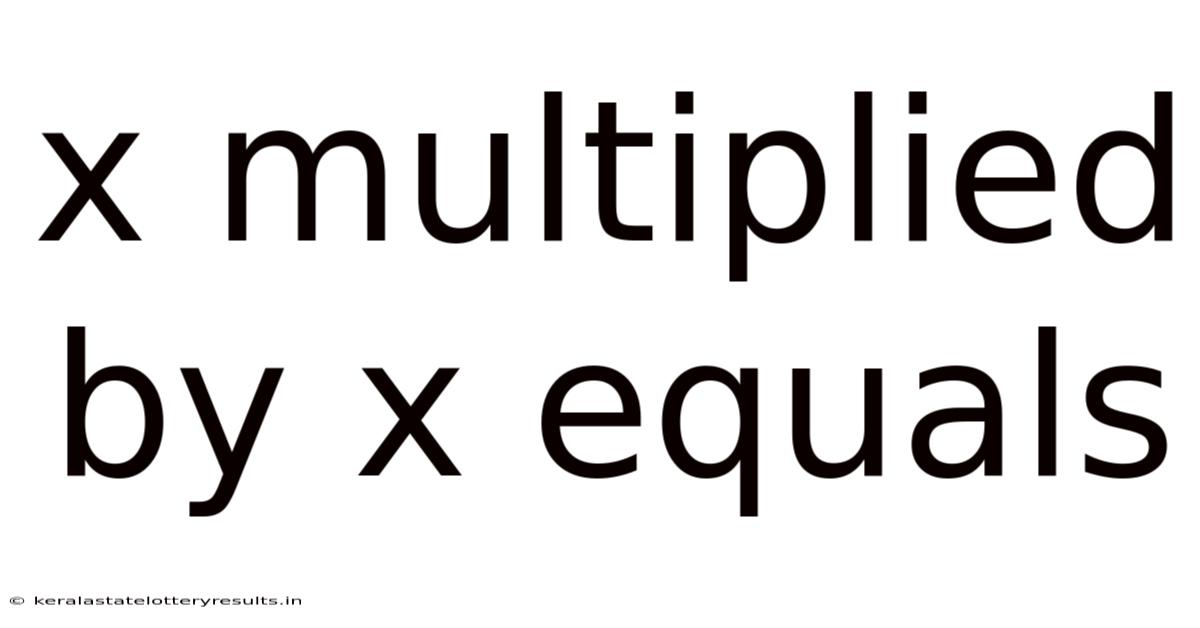
Table of Contents
X Multiplied by X: Exploring the Fundamentals of Squaring and its Applications
Understanding the concept of "x multiplied by x," often written as x², is fundamental to mathematics and numerous applications across various fields. This seemingly simple equation unlocks doors to higher-level mathematical concepts, offering insights into geometry, physics, computer science, and even finance. This comprehensive guide will explore the core meaning of x², delve into its applications, and address common questions surrounding this crucial mathematical operation.
Introduction: What Does X Multiplied by X Really Mean?
When we say "x multiplied by x," we are essentially performing a squaring operation. This means we are multiplying a number (represented by the variable x) by itself. The result, x², represents the square of x. It’s important to distinguish this from simply multiplying x by another number, say y, which would result in xy. In x², we are dealing with the same number multiplied by itself. This seemingly simple concept forms the bedrock of many complex mathematical ideas. Understanding it thoroughly is crucial for progress in various mathematical fields.
Understanding the Concept of Squaring
Let's break down the concept of squaring with some simple examples:
- If x = 2, then x² = 2 * 2 = 4
- If x = 5, then x² = 5 * 5 = 25
- If x = 10, then x² = 10 * 10 = 100
- If x = 0, then x² = 0 * 0 = 0
- If x = -3, then x² = (-3) * (-3) = 9 (Note that the square of a negative number is always positive).
Notice a pattern? The square of a number represents the area of a square with sides of that length. If you have a square with sides of length 3 units, its area is 3 * 3 = 9 square units. This geometrical interpretation provides a visual understanding of squaring, making it easier to grasp the concept.
Geometric Representation of X²
The geometric representation of x² is crucial for understanding its implications. Imagine a square with sides of length 'x'. The area of this square is calculated by multiplying the length of one side by the length of the other side. Since both sides have length 'x', the area is x * x = x². Therefore, x² represents the area of a square with sides of length x. This visual representation makes the concept intuitive and easy to understand, even for those who struggle with abstract mathematical concepts.
Algebraic Manipulation of X²
Understanding how to manipulate x² algebraically is crucial for solving equations and progressing in mathematics. Here are some key aspects:
- Expanding expressions: Expressions like (x + 2)² require expansion using the FOIL method (First, Outer, Inner, Last) or the binomial theorem: (x + 2)² = (x + 2)(x + 2) = x² + 4x + 4.
- Factoring expressions: This is the reverse of expanding. For example, factoring x² + 6x + 9 gives (x + 3)². Factoring is essential for solving quadratic equations.
- Solving quadratic equations: Equations involving x² are called quadratic equations. Solving them often requires techniques like factoring, completing the square, or using the quadratic formula. The solutions represent the values of x that make the equation true.
- Working with equations involving x²: Many mathematical problems involve equations where x² is a component. Understanding how to manipulate these equations correctly is key to finding solutions.
Applications of X²: Beyond the Basics
The concept of squaring, represented by x², has far-reaching applications in various fields:
1. Geometry and Trigonometry:
- Calculating areas: As discussed, x² directly calculates the area of a square. This extends to more complex shapes, where x² might represent a component of a larger area calculation.
- Pythagorean theorem: This fundamental theorem of geometry, a² + b² = c², relies heavily on squaring. It relates the lengths of the sides of a right-angled triangle.
- Trigonometry: Trigonometric functions often involve squaring values, particularly when dealing with identities and calculations involving the unit circle.
2. Physics:
- Calculating distances and areas: Many physics problems, particularly those involving projectile motion or calculating areas under curves, utilize the concept of squaring.
- Newton's second law of motion: Force (F) is often calculated as mass (m) times acceleration (a)².
- Energy calculations: Kinetic energy (KE) is calculated as ½mv², where v² represents the square of the velocity.
- Equations of motion: Many equations describing the motion of objects involve squared terms, particularly when dealing with acceleration.
3. Computer Science:
- Algorithms and data structures: Squared terms often appear in the analysis of algorithm efficiency (Big O notation), estimating the time or space complexity of algorithms.
- Graphics and game development: Calculating distances and positions on a screen often involves squaring coordinates.
- Cryptography: Some cryptographic algorithms utilize squaring operations in their encryption and decryption processes.
4. Finance and Economics:
- Compound interest calculations: The formula for compound interest involves exponential growth, often including squared or higher-powered terms.
- Statistical analysis: Variance and standard deviation calculations in statistics rely on squaring differences from the mean.
- Financial modeling: Many financial models incorporate squared terms to account for factors like risk and volatility.
Advanced Concepts Related to X²
The concept of x² forms the foundation for more advanced mathematical concepts:
- Higher powers: Cubing (x³) and raising to higher powers (x⁴, x⁵, etc.) are extensions of squaring. These higher powers have their own unique applications and interpretations.
- Polynomial functions: These functions contain terms with x raised to various powers, including x². Understanding x² is essential for understanding and manipulating polynomial functions.
- Calculus: The derivative and integral of x² are fundamental concepts in calculus, used for optimization and finding areas under curves.
- Complex numbers: Squaring also applies to complex numbers, where the concept extends to imaginary and complex planes.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between x² and 2x?
- A: x² represents x multiplied by itself (x * x), while 2x represents x multiplied by 2 (2 * x). They are fundamentally different operations with different results.
-
Q: Can x² ever be negative?
- A: No, the square of a real number (x) can never be negative. The square of a negative number is always positive. However, if we are dealing with complex numbers, the situation changes.
-
Q: How do I solve a quadratic equation involving x²?
- A: There are several methods for solving quadratic equations, including factoring, completing the square, and using the quadratic formula. The best method depends on the specific equation.
-
Q: What are the applications of x² in real-world situations?
- A: x² finds applications in a broad range of fields, including calculating areas and volumes in geometry, determining energy and motion in physics, analyzing algorithms in computer science, and modeling financial growth.
-
Q: Is there a limit to how large x² can be?
- A: No, there is no limit. As x increases, x² increases without bound.
Conclusion: The Enduring Importance of X²
The simple concept of "x multiplied by x," or x², while seemingly basic, is a cornerstone of mathematics and has profound implications across diverse fields. Its geometrical interpretation, algebraic manipulation, and widespread applications demonstrate its enduring importance. A solid understanding of x² is not just beneficial for mathematical proficiency; it's essential for tackling complex problems in various disciplines, from engineering and physics to finance and computer science. Mastering this fundamental concept unlocks a deeper understanding of the mathematical world and its real-world applications. By grasping the essence of squaring, you unlock a gateway to more advanced mathematical concepts and a broader perspective on the quantitative aspects of our world.
Latest Posts
Latest Posts
-
What Is 2 5 Of 1 2
Sep 15, 2025
-
When Was 8 Weeks Ago
Sep 15, 2025
-
4 To The Power 3
Sep 15, 2025
-
Is 112 A Prime Number
Sep 15, 2025
-
3 4 Of A Pound
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X Multiplied By X Equals . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.