What Is 2/5 Of 1/2
keralas
Sep 15, 2025 · 6 min read
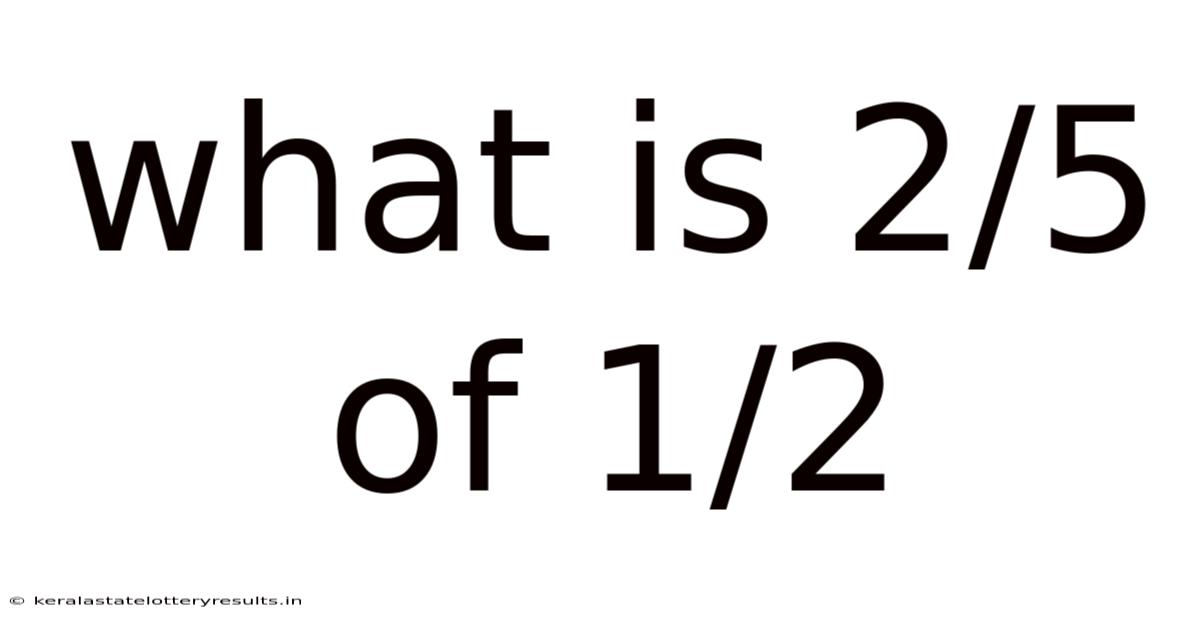
Table of Contents
Unveiling the Mystery: What is 2/5 of 1/2? A Deep Dive into Fraction Multiplication
Finding a fraction of a fraction might seem daunting at first, but it's a fundamental concept in mathematics with wide-ranging applications. This article will guide you through calculating "what is 2/5 of 1/2?" We'll break down the process step-by-step, explore the underlying mathematical principles, delve into real-world examples, and address frequently asked questions. By the end, you'll not only understand the solution but also possess a strong grasp of fraction multiplication. This is crucial for various fields, from cooking and sewing to engineering and finance.
Understanding Fractions: A Quick Refresher
Before we tackle the problem, let's review the basics of fractions. A fraction represents a part of a whole. It consists of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1 and the denominator is 2, representing one out of two equal parts.
Calculating 2/5 of 1/2: The Step-by-Step Approach
The phrase "2/5 of 1/2" translates directly into a multiplication problem: (2/5) x (1/2). Here's how to solve it:
Step 1: Multiply the Numerators
Multiply the numerators together: 2 x 1 = 2
Step 2: Multiply the Denominators
Multiply the denominators together: 5 x 2 = 10
Step 3: Form the Resultant Fraction
Combine the results from steps 1 and 2 to form the new fraction: 2/10
Step 4: Simplify the Fraction (If Possible)
The fraction 2/10 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 2 and 10 is 2. Divide both the numerator and the denominator by the GCD:
2 ÷ 2 = 1 10 ÷ 2 = 5
Therefore, the simplified fraction is 1/5.
Therefore, 2/5 of 1/2 is 1/5.
Visualizing the Problem: A Practical Approach
Imagine you have a pizza cut into 10 equal slices. 1/2 of the pizza represents 5 slices (10/2 = 5). Now, we want to find 2/5 of those 5 slices. This means we divide the 5 slices into 5 equal groups, and take 2 of those groups. Each group contains 1 slice (5/5 = 1), and taking 2 groups gives us 2 slices. These 2 slices represent 2/10 or 1/5 of the original pizza. This visual representation reinforces the mathematical calculation.
The Mathematical Principle Behind Fraction Multiplication
The method we used is a direct application of the rule for multiplying fractions:
(a/b) x (c/d) = (a x c) / (b x d)
Where 'a', 'b', 'c', and 'd' are integers, and 'b' and 'd' are not zero. This rule states that to multiply two fractions, we multiply the numerators together and the denominators together. The resulting fraction is then simplified if possible. This fundamental principle is applicable to all fraction multiplication problems.
Real-World Applications: Where Fraction Multiplication Matters
Understanding fraction multiplication is essential in various everyday situations:
-
Cooking and Baking: Recipes often require fractions of ingredients. If a recipe calls for 1/2 a cup of flour, and you want to make 2/3 of the recipe, you'll need to calculate (2/3) x (1/2) to determine the required amount of flour.
-
Sewing and Tailoring: Creating garments often involves precise measurements. If you need to reduce the length of a piece of fabric by 1/4, and the fabric is 2/3 of a yard long, you'll need to multiply fractions to find the new length.
-
Construction and Engineering: Precise calculations involving fractions are vital in construction and engineering. Determining the correct amount of materials or calculating precise measurements often involves fraction multiplication.
-
Finance and Budgeting: Managing finances requires a good understanding of fractions and percentages. Calculating a fraction of a budget or determining interest rates often involves fraction multiplication.
-
Data Analysis and Statistics: Understanding fractions is essential when analyzing data and interpreting statistical information. Many statistical calculations involve working with fractions and percentages.
Beyond the Basics: Extending Your Understanding
While the problem "2/5 of 1/2" might seem simple, it lays the groundwork for more complex fraction operations. This includes:
-
Multiplying more than two fractions: The principle remains the same; multiply all numerators together and all denominators together.
-
Multiplying mixed numbers: A mixed number (e.g., 1 1/2) is a combination of a whole number and a fraction. To multiply mixed numbers, convert them into improper fractions first (e.g., 1 1/2 becomes 3/2) and then follow the standard fraction multiplication rule.
-
Dividing fractions: Dividing by a fraction is equivalent to multiplying by its reciprocal. For example, dividing by 1/2 is the same as multiplying by 2/1 (or 2).
Frequently Asked Questions (FAQ)
Q: Can I multiply fractions in any order?
A: Yes, the commutative property of multiplication applies to fractions. This means that (2/5) x (1/2) is equal to (1/2) x (2/5). The order doesn't affect the final result.
Q: What if the fraction isn't easily simplified?
A: Even if the resulting fraction doesn't simplify easily to a smaller whole number, the fundamental calculation remains the same. You can use a calculator or long division to express the result as a decimal if necessary.
Q: Why is simplifying the fraction important?
A: Simplifying fractions makes the result easier to understand and interpret. A simplified fraction provides the most concise representation of the answer.
Q: Are there other ways to solve this problem?
A: While the standard multiplication method is the most efficient, you can also visualize the problem using diagrams or models. However, the mathematical calculation remains the same regardless of the chosen method.
Conclusion: Mastering Fractions for a Brighter Future
Mastering the concept of fraction multiplication is a cornerstone of mathematical literacy. The problem "What is 2/5 of 1/2?" might seem insignificant in isolation, but understanding the underlying principles empowers you to tackle more complex mathematical challenges in various aspects of life. From everyday tasks to professional endeavors, the ability to work confidently with fractions unlocks a world of opportunities. By thoroughly understanding this seemingly simple concept, you build a solid foundation for success in mathematics and beyond. Remember, practice is key to mastering fractions and enhancing your overall mathematical skills. Don’t hesitate to work through more examples to solidify your understanding and build confidence in your abilities.
Latest Posts
Latest Posts
-
Gcf Of 12 And 48
Sep 15, 2025
-
38 Degrees C To F
Sep 15, 2025
-
Is Diameter Half Of Radius
Sep 15, 2025
-
X 2 X 2 0
Sep 15, 2025
-
2to The Power Of 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/5 Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.