X 3 X 4 8
keralas
Sep 17, 2025 · 5 min read
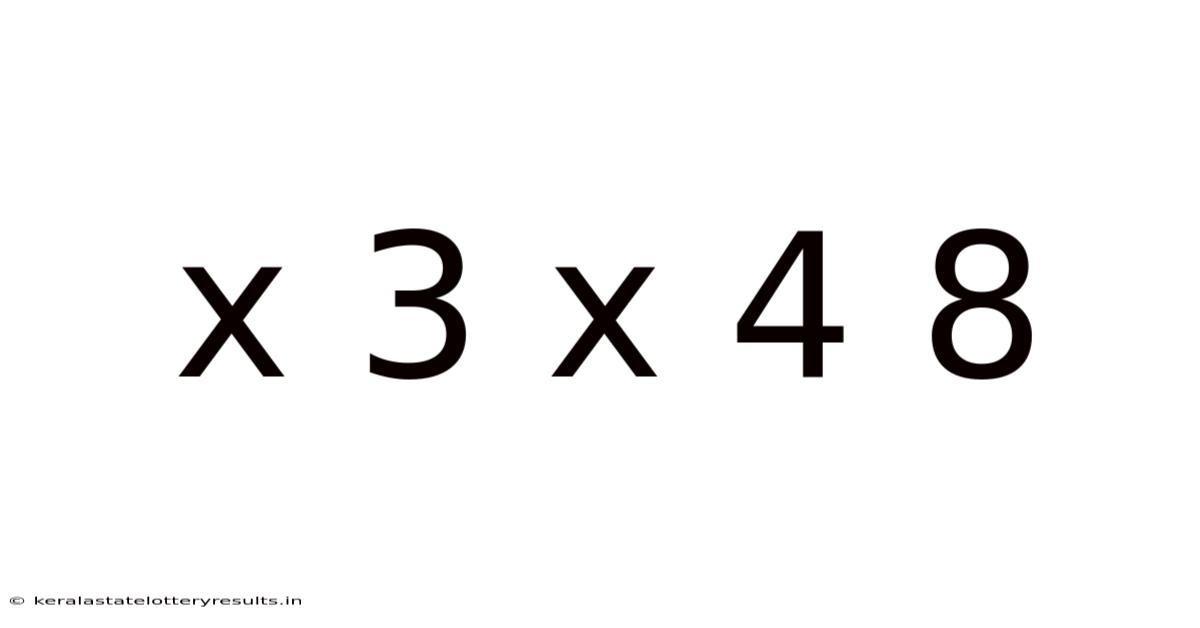
Table of Contents
Exploring the Mathematical Expression: x³ x⁴ = 8
This article delves into the mathematical expression x³ x⁴ = 8, exploring its solution, the underlying principles, and its applications. We'll unravel the seemingly simple equation to reveal a deeper understanding of exponents, algebraic manipulation, and problem-solving techniques. This exploration is suitable for students and anyone interested in strengthening their mathematical foundation.
Introduction: Understanding the Problem
The equation x³ x⁴ = 8 presents a classic example of an algebraic equation involving exponents. Understanding how to solve this equation requires knowledge of the rules of exponents, specifically the rule of multiplying exponential terms with the same base. The core concept lies in simplifying the equation to isolate the variable 'x' and then find its value. This process involves several steps, each building upon fundamental mathematical concepts. We'll dissect this process step-by-step, making it accessible to all levels of mathematical understanding. The solution will not only provide the answer but also a deeper understanding of the principles governing exponential equations.
Step-by-Step Solution
-
Applying the Rule of Exponents: The first crucial step is to simplify the left-hand side of the equation. Recall the rule for multiplying exponential terms with the same base: xᵃ xᵇ = x⁽ᵃ⁺ᵇ⁾. Applying this rule to our equation, we get:
x³ x⁴ = x⁽³⁺⁴⁾ = x⁷
Therefore, the simplified equation becomes:
x⁷ = 8
-
Finding the Seventh Root: Now, we need to isolate 'x'. Since 'x' is raised to the power of 7, we take the seventh root of both sides of the equation. This is the inverse operation of raising to the power of 7. This gives us:
⁷√x⁷ = ⁷√8
This simplifies to:
x = ⁷√8
-
Calculating the Seventh Root: Calculating the seventh root of 8 might not be immediately obvious. However, we can approach this by considering the prime factorization of 8. The prime factorization of 8 is 2³. Therefore, we can rewrite the equation as:
x = ⁷√(2³)
While we can't simplify this further to a whole number, we can express it as a radical or using decimal approximation. Using a calculator or mathematical software, we can determine the approximate value:
x ≈ 1.3459
Expanding on the Concepts: Exponents and Roots
Let's delve deeper into the mathematical concepts at play:
-
Exponents: Exponents (or powers) represent repeated multiplication. For instance, x³ means x * x * x, and x⁴ means x * x * x * x. Understanding this fundamental concept is crucial for working with exponential equations. The rules of exponents govern how we manipulate expressions with exponents, allowing for simplification and solution-finding.
-
Roots: Roots are the inverse operation of exponents. For example, the square root (√) of a number is a value that, when multiplied by itself, gives the original number. Similarly, the cube root (∛) is a value that, when multiplied by itself three times, gives the original number. Our equation involved the seventh root, which is a value that, when multiplied by itself seven times, equals the original number.
-
Prime Factorization: Prime factorization is the process of expressing a number as a product of its prime factors. This is particularly helpful in simplifying radical expressions. By factoring the number under the radical, we can sometimes simplify the expression and find exact solutions or approximations.
Solving Similar Equations: A Broader Perspective
The approach used to solve x³ x⁴ = 8 can be applied to a variety of similar equations involving exponents. For example, consider the equation:
x² x⁵ = 16
Following the same steps:
- Simplify: x² x⁵ = x⁷
- Isolate x: x⁷ = 16
- Take the Seventh Root: x = ⁷√16
Again, we can use a calculator or approximation methods to find the value of x. The key takeaway is the consistent application of the rules of exponents and the understanding of how to isolate the variable. The complexity may increase with higher exponents or more intricate equations, but the fundamental principles remain the same.
Applications in Real-World Scenarios
While this specific equation might not directly represent a real-world scenario in a straightforward manner, the underlying principles of exponential equations are widely applied in various fields:
-
Compound Interest: The growth of money in a savings account with compound interest follows an exponential pattern. Equations involving exponents are used to calculate the future value of an investment.
-
Population Growth: Exponential equations are frequently used to model population growth in biology and ecology. The rate of growth often follows an exponential pattern.
-
Radioactive Decay: The decay of radioactive materials follows an exponential pattern. Exponential equations are used to calculate the remaining amount of a radioactive substance after a specific time period.
-
Physics and Engineering: Exponential functions are crucial in various areas of physics and engineering, including modeling electrical circuits, heat transfer, and wave propagation.
These examples highlight the broad applicability of the mathematical concepts underlying our seemingly simple equation. Mastering these concepts opens doors to understanding and solving complex problems in various scientific and financial domains.
Frequently Asked Questions (FAQ)
-
Q: Can x³ x⁴ = 8 be solved without a calculator? A: Finding the exact value of the seventh root of 8 without a calculator is difficult. However, we can estimate the value or express it in radical form.
-
Q: What if the equation was x³ + x⁴ = 8? A: This is a different type of equation (a polynomial equation), and it requires different solution techniques. Solving this would involve more advanced algebraic methods.
-
Q: Are there other solutions besides the approximate value we found? A: For this specific equation, there's only one real solution (the approximate value of 1.3459). However, complex numbers could offer additional solutions in other scenarios involving higher-order equations.
-
Q: How do I improve my understanding of exponents and roots? A: Practice is key! Work through various exercises, explore different types of equations, and consult textbooks or online resources for a deeper understanding of the concepts.
Conclusion: Beyond the Equation
Solving the equation x³ x⁴ = 8 is more than just finding a numerical answer. It's about understanding the fundamental principles of exponents, roots, and algebraic manipulation. This seemingly simple equation serves as a gateway to a deeper understanding of mathematical concepts that have wide-ranging applications in various fields. By mastering these concepts, you not only improve your problem-solving skills but also gain a valuable foundation for more advanced mathematical studies. Remember to practice regularly, explore different problem sets, and don't hesitate to seek help when needed. The journey of learning mathematics is a continuous process of exploration and discovery.
Latest Posts
Latest Posts
-
Two Sample Z Test Formula
Sep 18, 2025
-
What Is A Multiplication Fact
Sep 18, 2025
-
What Is 20 Of 120
Sep 18, 2025
-
Number Of Oz In Quart
Sep 18, 2025
-
How To Find Vertical Intercept
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 4 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.