What Is 20 Of 120
keralas
Sep 18, 2025 · 5 min read
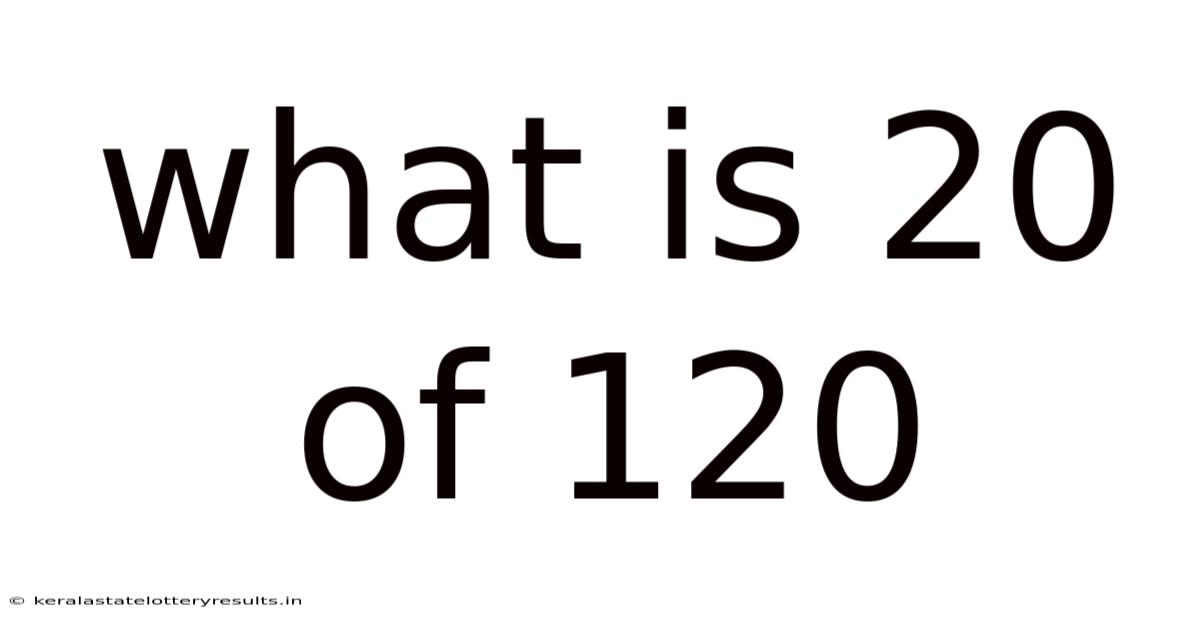
Table of Contents
What is 20 of 120? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 120?", opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. While the immediate answer might seem obvious, exploring the various ways to approach this problem illuminates important skills applicable across numerous fields, from everyday calculations to advanced mathematical modeling. This article will delve into different methods for solving this problem and explore the underlying principles involved.
Understanding the Question
The phrase "20 of 120" implies a relationship between two numbers. We're essentially asking what portion or fraction 20 represents when compared to 120. This can be interpreted in several ways, leading us to different mathematical operations.
Method 1: Finding the Fraction
The most straightforward approach is to express the relationship as a fraction. The number 20 is the part, and 120 is the whole. Therefore, the fraction is 20/120.
- Simplifying the Fraction: To understand the fraction better, we simplify it by finding the greatest common divisor (GCD) of 20 and 120. The GCD of 20 and 120 is 20. Dividing both the numerator and the denominator by 20, we get:
20/120 = 1/6
This simplified fraction, 1/6, tells us that 20 represents one-sixth of 120.
Method 2: Calculating the Percentage
Another common way to represent the relationship between 20 and 120 is as a percentage. A percentage expresses a fraction as a portion of 100. To calculate the percentage, we follow these steps:
- Form the fraction: As before, we form the fraction 20/120.
- Convert to a decimal: Divide the numerator (20) by the denominator (120): 20 ÷ 120 = 0.16666...
- Convert to a percentage: Multiply the decimal by 100: 0.16666... × 100 = 16.67% (approximately)
Therefore, 20 is approximately 16.67% of 120. The recurring decimal highlights the fact that this percentage is an approximation.
Method 3: Using Ratios
Ratios express the relationship between two quantities. The ratio of 20 to 120 can be written as 20:120 or 20/120. Similar to the fraction, we simplify this ratio by dividing both sides by their GCD (20):
20:120 = 1:6
This simplified ratio, 1:6, tells us that for every one unit of the first quantity, there are six units of the second quantity. This method is particularly useful when comparing relative sizes or proportions.
Expanding the Understanding: Applications and Further Exploration
The seemingly simple problem of determining "20 of 120" has led us to explore fundamental mathematical concepts. Let's expand on their applications and delve into more nuanced interpretations.
Real-World Applications:
- Sales and Discounts: Imagine a store offering a discount. If an item originally costs $120 and is discounted by $20, the discount is 20/120 or 16.67% off.
- Survey Results: If 20 out of 120 people surveyed preferred a particular product, then 1/6 or approximately 16.67% of respondents favored that product.
- Test Scores: If a student answered 20 questions correctly out of a total of 120, their score is 1/6 or approximately 16.67%.
- Ingredient Ratios: In cooking or chemistry, ratios are crucial. A recipe calling for a 1:6 ratio of ingredient A to ingredient B means for every one unit of A, you'd use six units of B. If you want to double the recipe, the ratio remains the same, just scaled up.
Deeper Dive into Mathematical Concepts:
- Proportions: The problem highlights the concept of proportions. A proportion is a statement that two ratios are equal. We can express the relationship as: 20/120 = x/100 (to find the percentage). Solving for x gives us the percentage value.
- Percentage Change: While we calculated the percentage of 20 within 120, we could also consider the percentage change if 20 was added to or subtracted from 120. This would involve a different calculation. The percentage increase from 100 to 120 is (120-100)/100 * 100% = 20%, for instance.
- Decimal Representation: Understanding decimal representation is key to accurately converting fractions and ratios to percentages. The recurring decimal in 0.1666... signifies a fraction that cannot be expressed exactly as a terminating decimal.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers were different? How would I approach "x of y"?
A: The same principles apply. To find what "x of y" is, you would create the fraction x/y, simplify it if possible, convert it to a decimal, and then multiply by 100 to get the percentage. Remember to always identify the part (x) and the whole (y).
-
Q: Is there a single "right" way to answer this question?
A: While the numerical result is consistent, different methods (fraction, percentage, ratio) offer varied insights into the relationship between the numbers. The best approach depends on the context and what you want to emphasize.
-
Q: What if the numbers weren't whole numbers?
A: The same principles apply. You'd still form the fraction, simplify it if possible, and convert to a decimal or percentage as needed. The calculations might involve more decimal places.
-
Q: How can I improve my understanding of fractions, percentages, and ratios?
A: Practice is key. Work through various examples, try different approaches, and focus on understanding the underlying concepts rather than just memorizing formulas. Use online resources, textbooks, or educational videos to further enhance your knowledge.
Conclusion
The question "What is 20 of 120?" serves as a springboard to explore fundamental mathematical concepts with broad applicability. By understanding fractions, percentages, and ratios, and their interrelationships, we develop valuable skills essential for problem-solving in various contexts. From everyday calculations to advanced mathematical applications, mastering these concepts empowers us to interpret data, make informed decisions, and engage with the numerical world more effectively. Remember that the beauty of mathematics lies not only in finding the answer but also in understanding the journey to arrive at that answer.
Latest Posts
Latest Posts
-
What Is A 6 8 Grade
Sep 18, 2025
-
Whats 20 Off Of 40
Sep 18, 2025
-
What Is Quarter Of 12
Sep 18, 2025
-
What Is 3 Times 8
Sep 18, 2025
-
70 Gbp In Us Dollars
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 120 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.