What's 3/4 As A Percent
keralas
Sep 16, 2025 · 6 min read
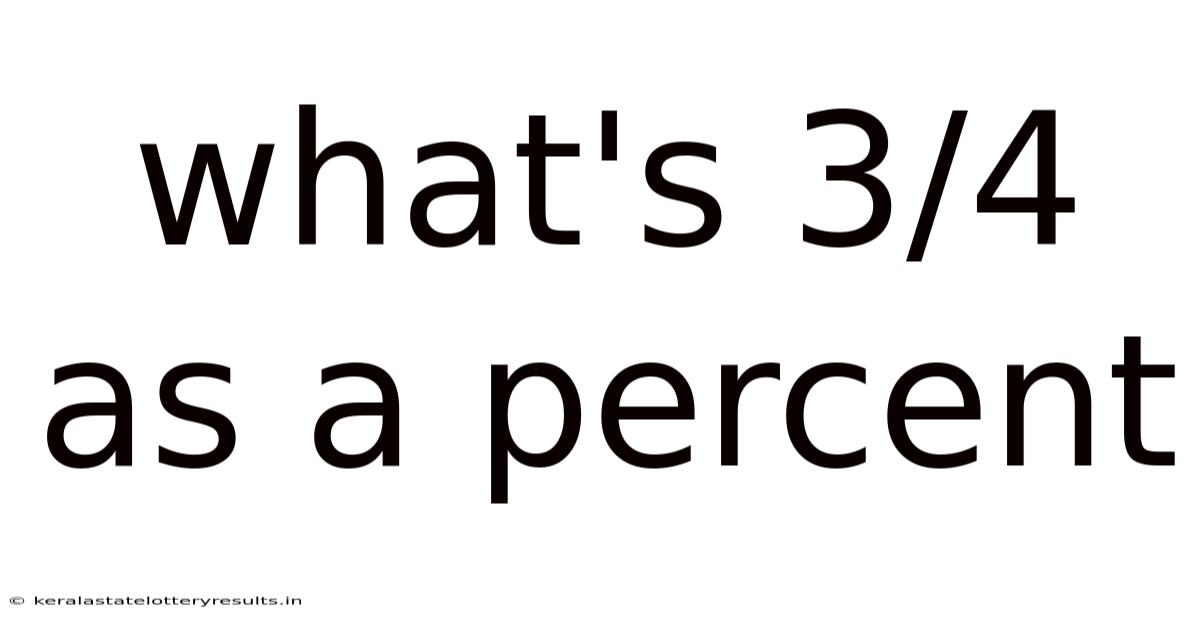
Table of Contents
What's 3/4 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts to understanding statistical data. This comprehensive guide will delve into the process of converting the fraction 3/4 into a percentage, explaining the underlying concepts and providing practical examples. We'll explore different methods, address common misconceptions, and equip you with the knowledge to confidently tackle similar conversions. By the end, you'll not only know that 3/4 is 75%, but you'll also understand why it is, and how to apply this knowledge to other fractions.
Understanding Fractions and Percentages
Before diving into the conversion, let's establish a clear understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 parts out of a possible 4.
A percentage, denoted by the symbol %, represents a fraction out of 100. It indicates how many parts out of 100 make up a whole. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Converting the Fraction to a Decimal
The most straightforward method for converting a fraction to a percentage involves two steps: first, converting the fraction to a decimal, and then converting the decimal to a percentage.
Step 1: Divide the numerator by the denominator
To convert 3/4 to a decimal, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Step 2: Multiply the decimal by 100%
Once we have the decimal equivalent (0.75), we multiply it by 100% to express it as a percentage:
0.75 x 100% = 75%
Therefore, 3/4 is equal to 75%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This method directly gives us the percentage since percentages are fractions out of 100.
Step 1: Determine the multiplication factor
We need to find a number that, when multiplied by the denominator (4), will result in 100. This is done by dividing 100 by the denominator:
100 ÷ 4 = 25
Step 2: Multiply both the numerator and the denominator by the multiplication factor
To maintain the value of the fraction, we must multiply both the numerator and the denominator by the same factor (25):
(3 x 25) / (4 x 25) = 75/100
Step 3: Express the fraction as a percentage
Since the denominator is now 100, the numerator directly represents the percentage:
75/100 = 75%
This method confirms that 3/4 is indeed equivalent to 75%.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the unknown percentage. We can set up a proportion where one ratio represents the fraction and the other represents the percentage.
Step 1: Set up the proportion
We can set up the proportion as follows:
3/4 = x/100
Where 'x' represents the unknown percentage.
Step 2: Cross-multiply and solve for x
Cross-multiplying the proportion gives us:
4x = 300
Dividing both sides by 4, we get:
x = 75
Therefore, x = 75%, confirming that 3/4 is equal to 75%.
Why is Understanding Fraction-to-Percentage Conversion Important?
The ability to convert fractions to percentages is a vital skill with numerous practical applications:
-
Calculating Discounts: Many sales are advertised as a percentage discount (e.g., 25% off). Converting the discount percentage back into a fraction helps calculate the final price.
-
Understanding Statistics: Statistical data is often presented as percentages. Understanding the underlying fractions helps to interpret the data more meaningfully.
-
Financial Literacy: Interest rates, taxes, and investment returns are often expressed as percentages. Converting percentages to fractions helps in comparing different financial options.
-
Everyday Calculations: From baking (measuring ingredients) to splitting bills, converting fractions to percentages can simplify everyday calculations.
-
Scientific Applications: In various scientific fields, converting fractions to percentages is essential for expressing experimental results and data analysis.
Common Mistakes to Avoid
While the conversion process seems straightforward, certain common mistakes can lead to inaccurate results:
-
Incorrect order of operations: When converting a fraction to a decimal, remember to divide the numerator by the denominator, not the other way around.
-
Forgetting to multiply by 100%: After obtaining the decimal equivalent, it's crucial to multiply by 100% to express the result as a percentage.
-
Incorrect simplification of fractions: Before converting, simplify the fraction to its lowest terms to make the calculation easier.
-
Misunderstanding the concept of percentage: Remember that a percentage is a fraction out of 100.
Further Exploration: Converting Other Fractions to Percentages
The methods described above can be applied to convert any fraction into a percentage. Let's look at a few examples:
-
1/2: 1 ÷ 2 = 0.5; 0.5 x 100% = 50%
-
2/5: 2 ÷ 5 = 0.4; 0.4 x 100% = 40%
-
7/8: 7 ÷ 8 = 0.875; 0.875 x 100% = 87.5%
-
1/3: 1 ÷ 3 = 0.333... (a recurring decimal); 0.333... x 100% ≈ 33.33% (approximately) Note that some fractions result in recurring decimals, requiring rounding for percentage representation.
Frequently Asked Questions (FAQ)
Q: Can I convert a mixed number (e.g., 1 1/4) to a percentage?
A: Yes, first convert the mixed number to an improper fraction (5/4 in this case), then use any of the methods described above to convert it to a percentage. 5/4 = 1.25; 1.25 x 100% = 125%
Q: What if the fraction has a very large denominator?
A: Using a calculator will simplify the process significantly, especially for fractions with large denominators. The principle of dividing the numerator by the denominator remains the same.
Q: Are there any online tools that can help with fraction-to-percentage conversion?
A: Many online calculators and conversion tools are available. However, understanding the underlying mathematical principles is crucial for solving problems independently.
Q: Why is understanding this concept important for real-world situations?
A: As explained previously, converting fractions to percentages is crucial for comprehending and applying numerical data in various real-world scenarios, including finance, shopping, and statistics.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with broad applications. The methods outlined in this guide – converting to a decimal, finding an equivalent fraction with a denominator of 100, and using proportions – offer different approaches to achieve the same result. By mastering these techniques, you will be well-equipped to confidently handle fraction-to-percentage conversions in various contexts. Remember to practice regularly to build your proficiency and understanding. The more you practice, the more effortless these conversions will become. Mastering this skill will undoubtedly enhance your mathematical abilities and contribute to a deeper understanding of numerical data.
Latest Posts
Latest Posts
-
Gcf Of 10 And 30
Sep 16, 2025
-
Is 18 Odd Or Even
Sep 16, 2025
-
Vertical Angles Are Congruent Proof
Sep 16, 2025
-
What Is 1 3 As Decimal
Sep 16, 2025
-
1 1 2 In Decimal Form
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What's 3/4 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.