Whats 25 Percent Of 50
keralas
Sep 12, 2025 · 6 min read
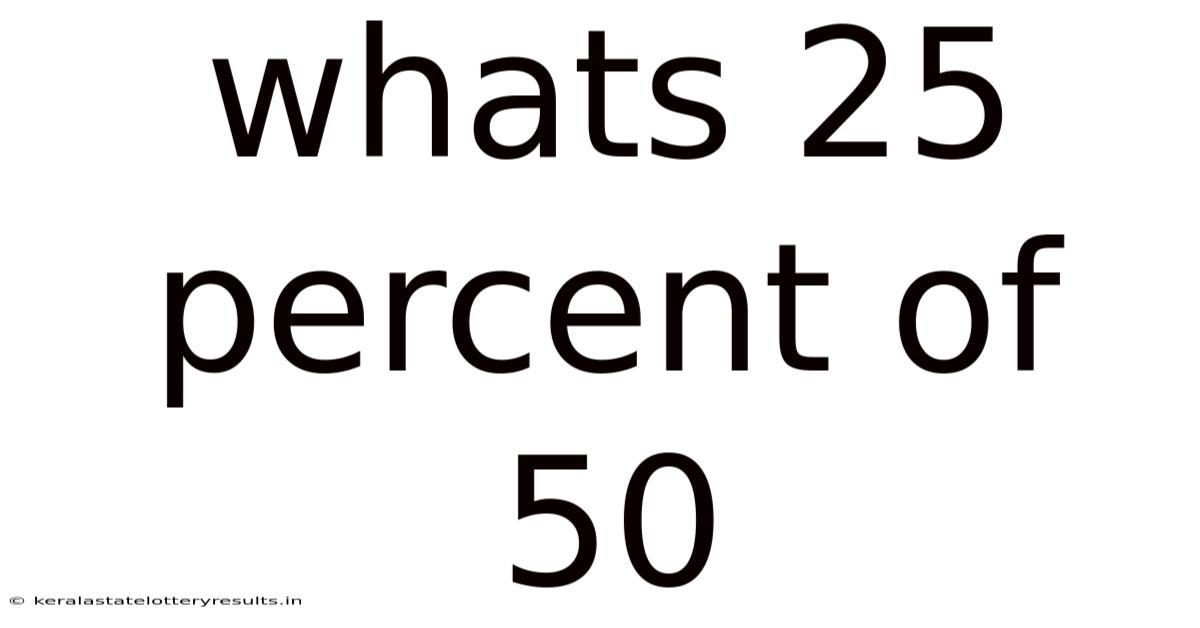
Table of Contents
What's 25 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 50 might seem like a simple calculation, but understanding the underlying principles of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and tips to understanding financial reports and statistical data. This article will not only answer the question "What's 25 percent of 50?" but also explore the broader concept of percentages, providing you with the tools to confidently tackle similar problems and delve deeper into the world of mathematics.
Understanding Percentages: A Foundation for Calculation
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25 percent (25%) means 25 out of 100, or 25/100. This fraction can be simplified to 1/4. This understanding forms the basis of all percentage calculations. We can use this fundamental concept to calculate 25% of 50, and many other percentage problems.
Calculating 25% of 50: Three Methods
There are several ways to calculate 25% of 50. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As we established, 25% is equivalent to 1/4. Therefore, finding 25% of 50 is the same as finding 1/4 of 50. This is a simple division problem:
50 ÷ 4 = 12.5
Therefore, 25% of 50 is 12.5.
Method 2: Converting Percentage to Decimal
Another approach involves converting the percentage to a decimal. To do this, divide the percentage by 100:
25% ÷ 100 = 0.25
Then, multiply this decimal by the number you want to find the percentage of:
0.25 x 50 = 12.5
Again, we arrive at the answer: 25% of 50 is 12.5.
Method 3: Using Proportions
A more formal approach utilizes proportions. We can set up a proportion to solve for the unknown value (x), which represents 25% of 50:
25/100 = x/50
To solve for x, we can cross-multiply:
25 x 50 = 100 x x
1250 = 100x
x = 1250/100
x = 12.5
This method reinforces the underlying relationship between percentages and fractions, highlighting the proportional nature of percentage calculations. The result, once again, confirms that 25% of 50 is 12.5.
Beyond the Basics: Practical Applications of Percentage Calculations
The ability to calculate percentages extends far beyond simple arithmetic exercises. Understanding percentages is crucial in numerous real-world scenarios:
-
Shopping and Discounts: Calculating discounts on sale items is a common application. If a store offers a 20% discount on a $100 item, you can easily calculate the discount and the final price using the methods described above.
-
Taxes and Tips: Determining sales tax or calculating a restaurant tip involves percentage calculations. Knowing how to calculate these amounts quickly and accurately is essential for managing personal finances.
-
Financial Literacy: Understanding interest rates on loans, credit cards, and savings accounts requires a firm grasp of percentages. This knowledge helps individuals make informed financial decisions.
-
Data Analysis and Statistics: Percentages are frequently used in data analysis to represent proportions and trends. Understanding percentages is critical for interpreting graphs, charts, and statistical reports.
-
Scientific and Engineering Applications: Percentages are used extensively in scientific research, engineering, and other fields to represent ratios, errors, and changes in quantities.
Advanced Percentage Calculations: Exploring More Complex Scenarios
While calculating 25% of 50 is straightforward, more complex scenarios may arise. Let's explore some examples:
-
Finding the Percentage One Number Represents of Another: Suppose you scored 45 out of 60 on a test. To determine your percentage score, you would divide your score by the total possible score and multiply by 100: (45/60) x 100 = 75%.
-
Calculating Percentage Increase or Decrease: If a stock price increased from $50 to $60, the percentage increase is calculated as follows: [(60-50)/50] x 100 = 20%. Similarly, a decrease can be calculated using the same formula.
-
Working with Compound Percentages: Compound interest, for example, involves calculating interest on the principal amount plus accumulated interest. This requires understanding how percentages build upon each other over time.
Addressing Common Misconceptions and Troubleshooting
Despite the seemingly simple nature of percentages, certain misconceptions can lead to errors. Here are a few common pitfalls to avoid:
-
Confusing Percentage and Decimal: Remembering to correctly convert between percentage and decimal form is crucial. Dividing the percentage by 100 before performing calculations is essential to obtain accurate results.
-
Incorrect Order of Operations: Following the correct order of operations (PEMDAS/BODMAS) is critical, especially when dealing with more complex percentage calculations involving multiple operations.
-
Rounding Errors: Rounding numbers prematurely can lead to inaccuracies in the final answer, especially when performing multiple calculations. It is advisable to maintain accuracy throughout the calculation process and round only at the very end.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase or decrease, subtract the original value from the new value, divide the result by the original value, and then multiply by 100.
Q: What is the difference between percentage points and percentage change?
A: Percentage points refer to the absolute difference between two percentages, while percentage change represents the relative change between two percentages. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% percentage increase.
Q: How can I improve my understanding of percentages?
A: Practice is key. Work through various examples, from simple to complex, and try different calculation methods. Use online resources, such as interactive calculators and tutorials, to reinforce your understanding.
Q: Are there any online tools that can help with percentage calculations?
A: Yes, many online percentage calculators are available. These calculators can perform various percentage calculations, making it easier to solve complex problems quickly and accurately. However, understanding the underlying principles remains crucial for applying percentage calculations in different contexts.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 25% of 50, while a simple problem, serves as a gateway to understanding the broader world of percentages. Mastering percentage calculations equips you with a valuable skill applicable to various aspects of life, from personal finance and shopping to data analysis and scientific endeavors. By understanding the fundamental concepts, exploring different calculation methods, and practicing regularly, you can develop confidence and proficiency in this crucial mathematical skill. The ability to confidently work with percentages empowers you to make informed decisions, solve problems effectively, and navigate the complexities of the modern world with greater ease and understanding. Remember, the journey to mastering percentages is a process of understanding, practice, and application. So keep practicing and keep learning!
Latest Posts
Latest Posts
-
Fastest Mile Per Hour Human
Sep 12, 2025
-
How Do You Times Percentages
Sep 12, 2025
-
Which Choices Are Real Numbers
Sep 12, 2025
-
Whats 5 8 As A Percent
Sep 12, 2025
-
4 1 8 To Decimal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.