Whats 5/8 As A Percent
keralas
Sep 12, 2025 · 5 min read
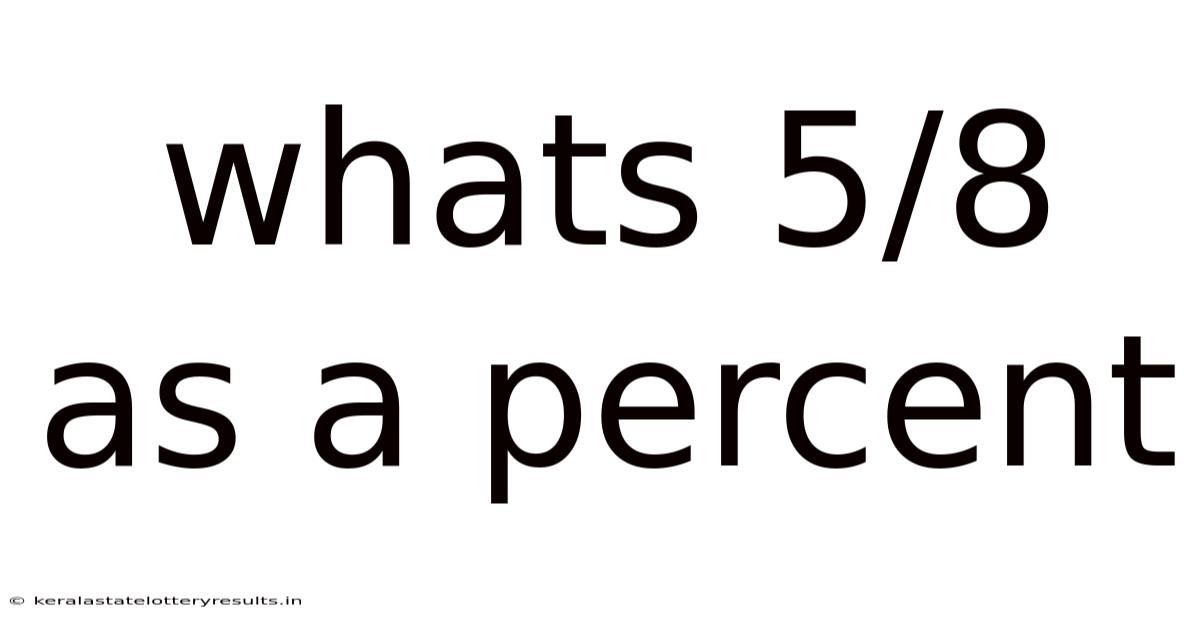
Table of Contents
What's 5/8 as a Percent? A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from everyday budgeting to advanced scientific calculations. This comprehensive guide will walk you through the process of converting 5/8 to a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll explore multiple methods, address common misconceptions, and answer frequently asked questions, making this a valuable resource for students and anyone looking to refresh their math skills.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 5/8 to a percentage, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). A percentage, on the other hand, represents a fraction of 100, indicated by the symbol %. For example, 50% means 50 out of 100, or 50/100. Converting fractions to percentages involves finding the equivalent percentage representation of a given fraction.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage is through division. Follow these steps:
-
Divide the numerator by the denominator: In our case, we divide 5 (numerator) by 8 (denominator): 5 ÷ 8 = 0.625
-
Multiply the result by 100: To express this decimal as a percentage, multiply the result by 100: 0.625 x 100 = 62.5
-
Add the percentage symbol: The final answer is 62.5%. Therefore, 5/8 is equal to 62.5%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction where the denominator is 100. This method is particularly useful when dealing with fractions that can be easily simplified to have a denominator of 100 or a factor of 100. While not as direct as the division method, it provides a valuable understanding of fraction equivalence.
Unfortunately, 5/8 cannot be easily converted to an equivalent fraction with a denominator of 100. The denominator 8 does not divide evenly into 100. However, this method is valuable for understanding the principles of fraction equivalence and is often easier to use with fractions that have denominators which are factors of 100 (like 2, 4, 5, 10, 20, 25, 50). Let's illustrate with an example using a fraction that can be easily converted using this method:
Let's convert 1/4 to a percentage. We need to find an equivalent fraction with a denominator of 100:
-
Determine the multiplier: To change the denominator from 4 to 100, we multiply by 25 (100 ÷ 4 = 25).
-
Multiply both the numerator and the denominator by the multiplier: We multiply both the numerator and denominator of 1/4 by 25: (1 x 25) / (4 x 25) = 25/100
-
Express as a percentage: 25/100 is equivalent to 25%.
This method reinforces the concept that multiplying or dividing both the numerator and denominator of a fraction by the same number does not change its value.
Method 3: Using Proportions
This method utilizes the concept of proportions to solve for the percentage. A proportion is an equation stating that two ratios are equal. We can set up a proportion to solve for the percentage equivalent of 5/8:
-
Set up the proportion: We set up a proportion where x represents the unknown percentage:
5/8 = x/100
-
Cross-multiply: To solve for x, we cross-multiply:
8x = 500
-
Solve for x: We divide both sides by 8:
x = 500/8 = 62.5
-
Add the percentage symbol: The answer is 62.5%.
Understanding the Result: 62.5%
The result, 62.5%, signifies that 5/8 represents 62.5 parts out of 100. This is a crucial concept for interpreting the relative size of fractions and understanding their proportional relationships. It allows us to compare fractions easily and understand their magnitude relative to a whole.
Practical Applications of Fraction-to-Percentage Conversion
Converting fractions to percentages has numerous practical applications:
-
Calculating discounts: Determining the actual price after a percentage discount requires converting the discount fraction to a percentage.
-
Analyzing data: Representing data as percentages makes comparisons and interpretations much easier. For example, in survey results, expressing responses as percentages provides a clear overview of the distribution.
-
Financial calculations: Interest rates, tax calculations, and profit margins are often expressed as percentages.
-
Scientific measurements: Many scientific calculations involve converting fractions to percentages for easier analysis and representation of data.
Common Misconceptions
One common misconception is believing that simply multiplying the numerator by 100 gives the percentage. This is incorrect. You must divide the numerator by the denominator before multiplying by 100. This crucial step accounts for the relative size of the fraction compared to the whole.
Frequently Asked Questions (FAQ)
-
Can all fractions be converted to percentages? Yes, all fractions can be converted to percentages by dividing the numerator by the denominator and multiplying by 100.
-
What if the resulting percentage has a decimal? A decimal in the percentage is perfectly acceptable. For example, 62.5% is a perfectly valid percentage.
-
Are there other ways to convert fractions to percentages? While the methods described above are the most common and straightforward, more advanced techniques exist, particularly for more complex fractions.
-
How can I improve my skills in converting fractions to percentages? Practice is key! The more you practice converting various fractions to percentages using different methods, the more confident and proficient you will become.
Conclusion: Mastering Fraction-to-Percentage Conversions
Mastering the conversion of fractions to percentages is an essential skill that significantly enhances mathematical understanding and problem-solving capabilities. By understanding the different methods, their underlying principles, and addressing common misconceptions, you can confidently handle various real-world scenarios requiring this conversion. Remember that practice is crucial to strengthening your skills and building a strong foundation in this fundamental mathematical concept. Whether you're a student tackling homework, a professional analyzing data, or simply someone looking to enhance your math skills, understanding how to convert 5/8 (or any fraction) to a percentage is a valuable asset. The ability to easily move between these different representations of numbers is a hallmark of mathematical fluency.
Latest Posts
Latest Posts
-
Is Length Or Width First
Sep 13, 2025
-
44 Out Of 50 Percentage
Sep 13, 2025
-
Integration Of An Absolute Value
Sep 13, 2025
-
All The Factors Of 98
Sep 13, 2025
-
Angles And Pairs Of Angles
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about Whats 5/8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.