Whats 25 Percent Of 40
keralas
Sep 12, 2025 · 5 min read
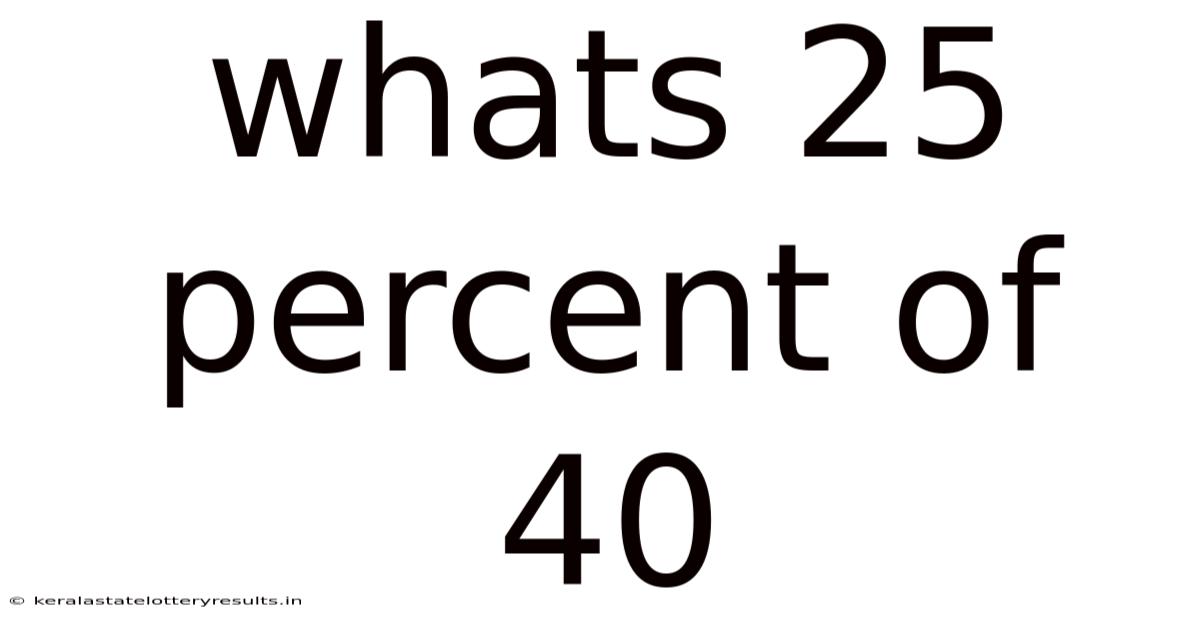
Table of Contents
What's 25 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 40 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This seemingly basic calculation has far-reaching applications in various fields, from everyday finances to complex scientific analyses. This article will not only answer the question "What's 25 percent of 40?" but will also explore the underlying principles of percentage calculations, different methods for solving percentage problems, and real-world examples demonstrating their importance.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." So, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. This fractional representation is key to understanding how percentages work.
Method 1: Using the Fraction Method
The simplest way to calculate 25% of 40 is to use the fractional equivalent of 25%. As we established, 25% is equal to 1/4. Therefore, finding 25% of 40 is the same as finding 1/4 of 40. This is a straightforward division:
40 / 4 = 10
Therefore, 25% of 40 is 10.
Method 2: Using Decimal Conversion
Another common method involves converting the percentage to a decimal. To do this, divide the percentage by 100. 25% divided by 100 is 0.25. Then, multiply this decimal by the number you're finding the percentage of:
0.25 * 40 = 10
This method provides the same result: 25% of 40 is 10.
Method 3: Using Proportion
A more formal approach uses proportions. A proportion sets up an equivalence between two ratios. We can set up a proportion as follows:
X/40 = 25/100
Where X represents the unknown value (25% of 40). To solve for X, we can cross-multiply:
100X = 25 * 40 100X = 1000 X = 1000 / 100 X = 10
Again, we arrive at the answer: 25% of 40 is 10.
Why Understanding Percentages is Crucial
The ability to calculate percentages is a fundamental skill applicable across numerous aspects of life:
-
Finance: Calculating discounts, sales tax, interest rates, tips, and profit margins all rely heavily on percentage calculations. Understanding percentages helps make informed financial decisions, whether it's budgeting, investing, or negotiating prices. For example, if a $100 item is discounted by 20%, you can easily calculate the final price.
-
Science: Percentages are used extensively in scientific research and data analysis to represent proportions, errors, and changes in quantities. For instance, expressing the percentage increase or decrease in a population, the percentage of a specific element in a compound, or the percentage of successful trials in an experiment all require accurate percentage calculations.
-
Everyday Life: Percentages appear in numerous everyday situations. Understanding them helps you comprehend statistics presented in news reports, understand the nutritional information on food labels, interpret survey results, and even calculate the tip at a restaurant.
Advanced Percentage Calculations: Beyond the Basics
While the calculation of 25% of 40 is straightforward, the principles can be extended to more complex scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to determine what percentage one number is of another. For example, "What percentage of 80 is 20?" This involves setting up a proportion: X/100 = 20/80, solving for X to find that 20 is 25% of 80.
-
Finding the Original Number: Sometimes, you know the percentage and the resulting value, and need to find the original number. For example, "A product is discounted by 30% and now costs $70. What was the original price?" This requires working backward using the percentage and the final price.
-
Percentage Change: This involves calculating the percentage increase or decrease between two numbers. The formula is: (New Value - Old Value) / Old Value * 100%. Understanding percentage change is vital for tracking trends in various data sets.
-
Compound Interest: This involves calculating interest earned on both the principal amount and accumulated interest. The formula is more complex, but the underlying principle still involves percentages.
Real-World Applications: Examples
Let's look at a few real-world examples to illustrate the practical applications of percentage calculations:
-
Sales Tax: Suppose a shirt costs $40, and the sales tax is 6%. To calculate the total cost, you would find 6% of $40 (0.06 * $40 = $2.40) and add it to the original price ($40 + $2.40 = $42.40).
-
Discounts: A store offers a 25% discount on a $120 item. The discount amount is 25% of $120 (0.25 * $120 = $30), making the final price $90.
-
Tips: If you want to leave a 15% tip on a $60 restaurant bill, you'd calculate 15% of $60 (0.15 * $60 = $9) and add it to the bill.
-
Grade Calculation: If you scored 85 out of 100 on a test, your percentage score is 85% (85/100 * 100%).
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that isn't a whole number, like 12.5%?
A: You can use the same methods as described above. Convert 12.5% to a decimal (0.125) and multiply it by the number.
Q: Are there online calculators or software tools that can help with percentage calculations?
A: Yes, many free online calculators are available that can perform percentage calculations. These are helpful for quick calculations and checking your work.
Q: How can I improve my understanding of percentages?
A: Practice is key! Work through various percentage problems, starting with simple ones and gradually moving to more complex calculations. Try to understand the underlying principles and apply them in real-world contexts. You can find numerous practice exercises online or in textbooks.
Conclusion
Finding 25% of 40, while seemingly trivial, provides a gateway to understanding the essential role of percentages in various aspects of life. Mastering percentage calculations enhances your problem-solving skills, making you more confident and proficient in tackling numerical challenges in finance, science, and everyday situations. The methods outlined in this article – using fractions, decimals, or proportions – provide a strong foundation for understanding and applying percentage calculations effectively. Remember that consistent practice is the key to developing fluency in working with percentages. The more you work with them, the more intuitive they will become.
Latest Posts
Latest Posts
-
1 Sample T Test Formula
Sep 12, 2025
-
115 Degrees F To C
Sep 12, 2025
-
What Is 15 Of 50
Sep 12, 2025
-
Win Loss Tie Percentage Calculator
Sep 12, 2025
-
What Is 25 Of 2000
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.