What Is 25 Of 2000
keralas
Sep 12, 2025 · 6 min read
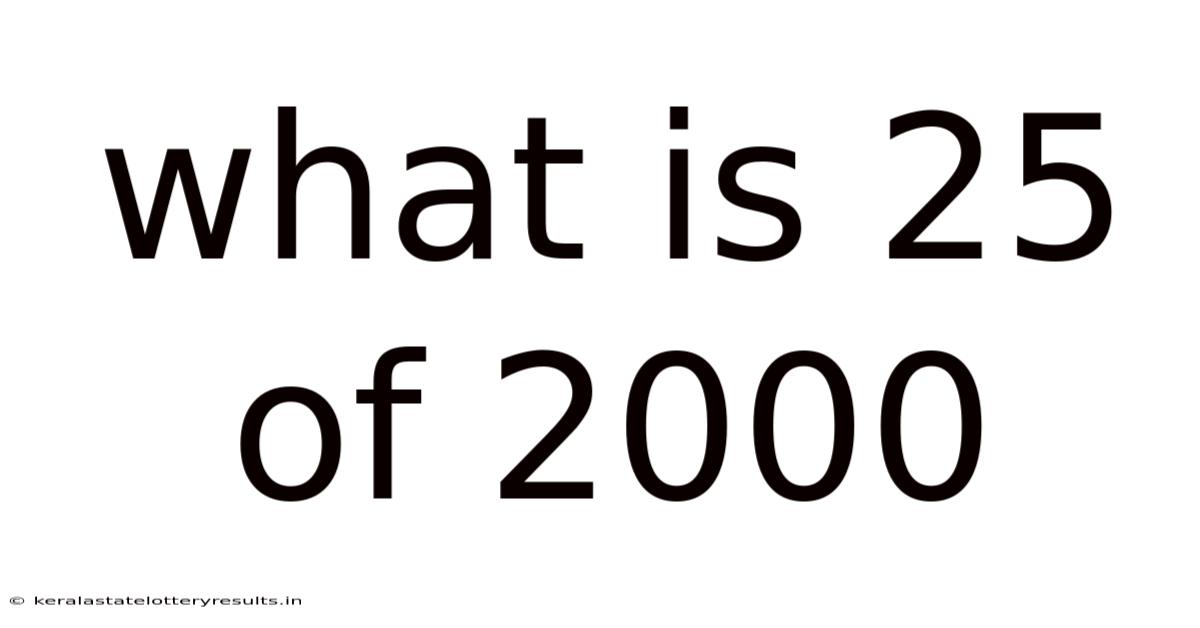
Table of Contents
What is 25% of 2000? A Deep Dive into Percentages and Their Applications
Finding 25% of 2000 might seem like a simple calculation, suitable only for elementary school students. However, understanding how to solve this problem unlocks a broader comprehension of percentages, a concept fundamental to numerous aspects of daily life, from finance and budgeting to scientific analysis and data interpretation. This article will not only provide the answer but also explore the underlying principles, various methods of calculation, and real-world applications of percentages, making it a comprehensive guide for anyone wanting to master this crucial mathematical skill.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "per hundred" – it represents parts of a whole. The symbol "%" is used to denote percentages. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
Understanding percentages is crucial for interpreting data, making comparisons, and understanding proportions. They are ubiquitously used to express discounts, tax rates, interest rates, growth rates, and much more. Mastering percentage calculations empowers you to make informed decisions in various aspects of your life.
Calculating 25% of 2000: Three Methods
There are several ways to calculate 25% of 2000. Let's explore three common and effective methods:
Method 1: Using the Fraction Equivalent
25% can be expressed as the fraction 25/100. This simplifies to 1/4. Therefore, finding 25% of 2000 is equivalent to finding 1/4 of 2000. This is a simple division:
2000 / 4 = 500
Therefore, 25% of 2000 is 500.
Method 2: Converting Percentage to Decimal
To convert a percentage to a decimal, divide the percentage by 100. In this case:
25% / 100 = 0.25
Now, multiply this decimal by the number you want to find the percentage of:
0.25 * 2000 = 500
Again, we arrive at the answer: 500. This method is particularly useful when working with more complex percentages or when using calculators.
Method 3: Using Proportions
Percentages can be understood as a proportion. We can set up a proportion to solve for the unknown value:
25/100 = x/2000
Where 'x' represents 25% of 2000. To solve for x, we can cross-multiply:
25 * 2000 = 100 * x
50000 = 100x
x = 50000 / 100
x = 500
This confirms our answer: 500. The proportion method offers a more formal and adaptable approach, especially useful when dealing with more intricate percentage problems.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a multitude of real-life situations. Here are a few examples:
-
Finance and Budgeting: Calculating interest earned on savings accounts, determining the amount of sales tax on a purchase, understanding loan interest rates, calculating discounts on sale items, and managing personal finances all require a thorough understanding of percentages. For example, if a house costs $2000,000 and requires a 25% down payment, that would be $500,000.
-
Sales and Marketing: Businesses use percentages extensively to track sales growth, determine profit margins, analyze market share, and calculate discounts and promotional offers. Understanding percentage change is crucial for analyzing trends and making informed business decisions. A 25% increase in sales, for example, demonstrates significant growth.
-
Science and Data Analysis: Percentages are frequently used to express statistical data, such as the percentage of a population with a certain characteristic, or the percentage change in a scientific measurement over time. Researchers use percentages to represent and analyze data from experiments and surveys. For example, if 25% of a sample of 2000 mice showed resistance to a certain disease, it would imply that 500 mice showed resistance.
-
Education and Grading: Grading systems often use percentages to represent student performance. A score of 80% on an exam signifies that a student answered 80 out of 100 questions correctly. Understanding percentages allows students to effectively gauge their progress and areas of improvement.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels (percentage of daily value for various nutrients), and comprehending statistics presented in news reports all necessitate a grasp of percentage calculations.
Beyond the Basics: Percentage Increase and Decrease
While calculating a percentage of a number is fundamental, understanding percentage increases and decreases is equally crucial. These concepts involve finding the difference between an original value and a new value, expressed as a percentage of the original value.
Percentage Increase: This calculates the increase in a value as a percentage of the original value. The formula is:
[(New Value - Original Value) / Original Value] * 100%
For example, if a stock price increases from $1000 to $1250, the percentage increase is:
[(1250 - 1000) / 1000] * 100% = 25%
Percentage Decrease: This calculates the decrease in a value as a percentage of the original value. The formula is:
[(Original Value - New Value) / Original Value] * 100%
If the stock price decreases from $1250 to $1000, the percentage decrease is:
[(1250 - 1000) / 1250] * 100% = 20%
Note that percentage increase and decrease are not necessarily inverse operations.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common mistakes include incorrectly converting percentages to decimals, dividing by the wrong number, or misunderstanding the context of the problem (e.g., calculating percentage increase versus percentage of a whole). Always double-check your work and ensure you understand what the problem is asking for.
Q: How can I improve my skills in calculating percentages quickly and accurately?
A: Practice regularly with a variety of problems. Start with simple examples and gradually work towards more complex calculations. Use different methods to solve the same problem to reinforce your understanding. Memorizing some common percentage equivalents (like 25% = 1/4, 50% = 1/2, 75% = 3/4) can also improve speed.
Q: Are there any online tools or calculators that can help with percentage calculations?
A: Yes, many online calculators are available that can perform percentage calculations quickly and easily. These can be helpful for checking your work or for tackling more complex problems. However, understanding the underlying principles is crucial for effective problem-solving.
Q: How are percentages used in compound interest calculations?
A: Compound interest involves earning interest not only on the principal amount but also on accumulated interest. Percentages are used to determine the interest rate applied to the balance at each compounding period. The formula for compound interest incorporates percentages directly.
Conclusion
Calculating 25% of 2000, while seemingly simple, serves as a gateway to understanding the broader applications of percentages in various fields. This article has demonstrated multiple methods for calculating percentages and explored their significance in diverse contexts. By mastering these techniques and grasping the underlying concepts, you equip yourself with a powerful tool for tackling mathematical problems and making informed decisions in your personal and professional life. Remember, the key is consistent practice and a thorough understanding of the principles involved. With enough practice, even complex percentage calculations will become straightforward and intuitive.
Latest Posts
Latest Posts
-
How Many Lbs Is 78kg
Sep 12, 2025
-
Square Root Of 24 Simplified
Sep 12, 2025
-
4 5 Cm How Many Inches
Sep 12, 2025
-
Convert 170 C To F
Sep 12, 2025
-
50 With 40 Percent Off
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.