Whats 20 Percent Of 40
keralas
Sep 12, 2025 · 6 min read
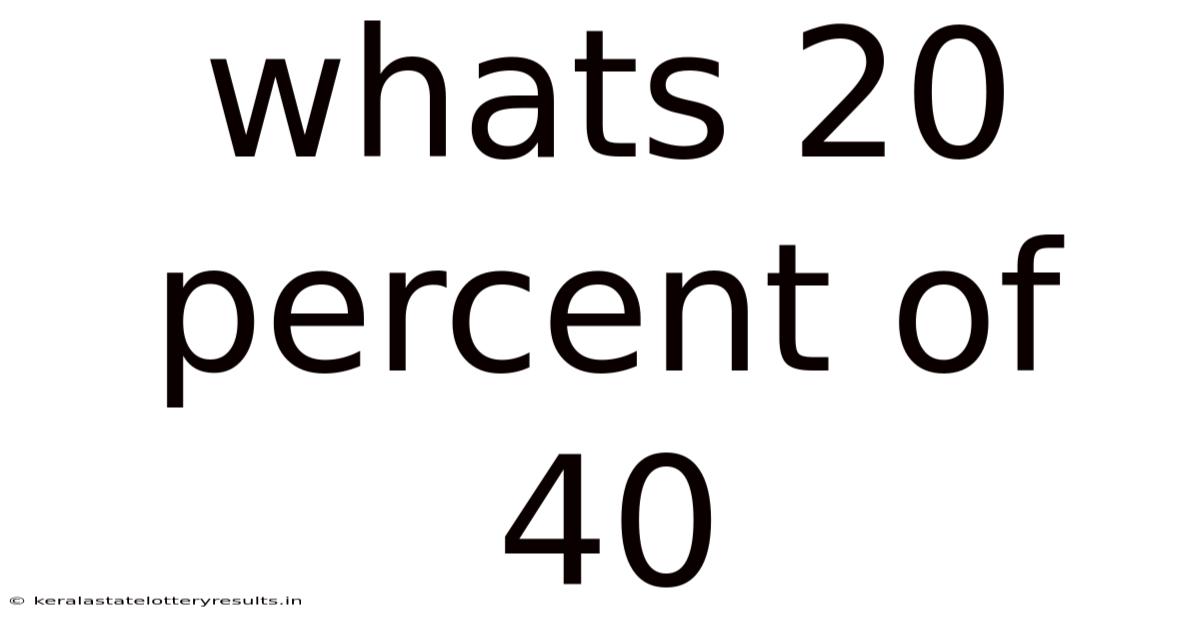
Table of Contents
What's 20 Percent of 40? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 40 might seem like a simple calculation, easily solved with a quick bit of mental math or a calculator. However, understanding the underlying principles of percentages and their widespread applications is far more valuable. This article will not only answer the question "What's 20 percent of 40?" but will also explore the concept of percentages, different methods of calculation, and real-world examples where this fundamental mathematical skill is essential.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." When we say "20 percent," we are referring to 20 parts out of a total of 100 parts. This can be represented as a fraction (20/100), a decimal (0.20), or, of course, as a percentage (20%).
Understanding this basic definition is crucial to mastering percentage calculations. It lays the groundwork for tackling more complex problems involving discounts, tax calculations, interest rates, and much more.
Calculating 20 Percent of 40: Three Simple Methods
There are several ways to calculate 20 percent of 40. Let's explore three common methods:
1. The Fraction Method:
This method utilizes the fractional representation of a percentage. Since 20 percent is equivalent to 20/100, we can set up the calculation as follows:
(20/100) * 40 = 8
We simply multiply the fraction by the whole number (40). This method directly applies the definition of percentage as a fraction of 100.
2. The Decimal Method:
This method converts the percentage to its decimal equivalent. To convert 20% to a decimal, we divide by 100:
20% / 100 = 0.20
Now we multiply this decimal by 40:
0.20 * 40 = 8
The decimal method is often preferred for its ease of use with calculators.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value. We can express the problem as:
20/100 = x/40
Where 'x' represents 20% of 40. To solve for 'x', we cross-multiply:
20 * 40 = 100 * x 800 = 100x x = 800/100 x = 8
This method is particularly useful for more complex percentage problems where the relationships between different quantities are important.
Therefore, 20 percent of 40 is 8.
Beyond the Basics: Applying Percentage Calculations in Real Life
The ability to calculate percentages is a vital life skill, applicable in numerous situations:
-
Shopping and Discounts: Calculating discounts is a prime example. If a $40 item is on sale for 20% off, you'll save $8 (as we've just calculated!), resulting in a final price of $32. Understanding percentage discounts allows you to make informed purchasing decisions and find the best deals.
-
Taxes and Interest: Sales tax, income tax, and interest rates are all expressed as percentages. For example, a 6% sales tax on a $100 purchase is calculated as 0.06 * $100 = $6. Similarly, calculating interest earned on savings accounts or interest accrued on loans requires a solid grasp of percentages.
-
Tip Calculations: When dining out, calculating a tip is a common application of percentages. A 15% tip on a $50 bill, for example, would be 0.15 * $50 = $7.50.
-
Grading and Statistics: Percentages are widely used in education to express grades (e.g., scoring 80% on a test). In statistics, percentages are essential for representing proportions and probabilities within data sets. Understanding percentages helps you interpret data more effectively.
-
Finance and Investments: Calculating returns on investments, understanding stock market fluctuations, and assessing the risk associated with different financial instruments all heavily rely on percentage calculations. Financial literacy requires a strong foundation in percentage mathematics.
Advanced Percentage Calculations: A Glimpse into More Complex Scenarios
While calculating 20% of 40 is relatively straightforward, percentage calculations can become more complex. Let's briefly explore some scenarios:
-
Finding the Percentage: Instead of finding a percentage of a number, you might need to find what percentage one number is of another. For example, what percentage of 50 is 10? This requires dividing 10 by 50 and multiplying by 100 (10/50 * 100 = 20%).
-
Percentage Increase and Decrease: These calculations involve finding the percentage change between two numbers. For example, if a price increases from $20 to $25, the percentage increase is calculated as ((25-20)/20) * 100 = 25%.
-
Compound Interest: Compound interest involves earning interest on both the principal amount and the accumulated interest. This requires repeated percentage calculations over time, resulting in exponential growth.
-
Percentage Points vs. Percentages: It's crucial to differentiate between these two terms. A percentage point refers to an absolute difference between two percentages, while a percentage refers to a relative change. For example, an increase from 10% to 15% is a 5 percentage point increase, but a 50% relative increase ((15-10)/10 * 100 = 50%).
Troubleshooting Common Mistakes
Several common mistakes can arise when working with percentages:
-
Incorrect Decimal Conversion: Failing to correctly convert a percentage to a decimal (e.g., confusing 10% with 10 instead of 0.10) is a frequent error. Always remember to divide the percentage by 100 before performing calculations.
-
Misinterpreting the Problem: Carefully read the problem statement to ensure you understand what is being asked. Identifying whether you need to find a percentage of a number, find what percentage one number represents of another, or calculate a percentage increase/decrease is crucial.
-
Calculation Errors: Double-check your calculations, especially when dealing with multiple steps. Use a calculator if necessary to minimize the risk of arithmetic errors.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase?
-
A: Subtract the original value from the new value, divide the result by the original value, and multiply by 100.
-
Q: How do I calculate a percentage decrease?
-
A: Subtract the new value from the original value, divide the result by the original value, and multiply by 100. The answer will be negative indicating a decrease.
-
Q: What is the difference between percentage and percentage points?
-
A: Percentage points represent an absolute change in percentage values, while percentages represent a relative change.
-
Q: How can I improve my percentage calculation skills?
-
A: Practice regularly with various problems, use different calculation methods, and check your answers carefully. Online resources and practice worksheets can be helpful.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not just about solving simple math problems; it's about developing a crucial life skill. From managing finances to interpreting data, the ability to confidently and accurately work with percentages opens doors to greater understanding and success in numerous aspects of life. While calculating 20% of 40 is a basic step, mastering this fundamental concept paves the way for tackling more complex calculations and making informed decisions in a world filled with numerical data. So, keep practicing, and you'll soon find yourself effortlessly navigating the world of percentages.
Latest Posts
Latest Posts
-
115 Degrees F To C
Sep 12, 2025
-
What Is 15 Of 50
Sep 12, 2025
-
Win Loss Tie Percentage Calculator
Sep 12, 2025
-
What Is 25 Of 2000
Sep 12, 2025
-
Write P In Factored Form
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Whats 20 Percent Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.