What Is 1/3 / 2
keralas
Sep 16, 2025 · 5 min read
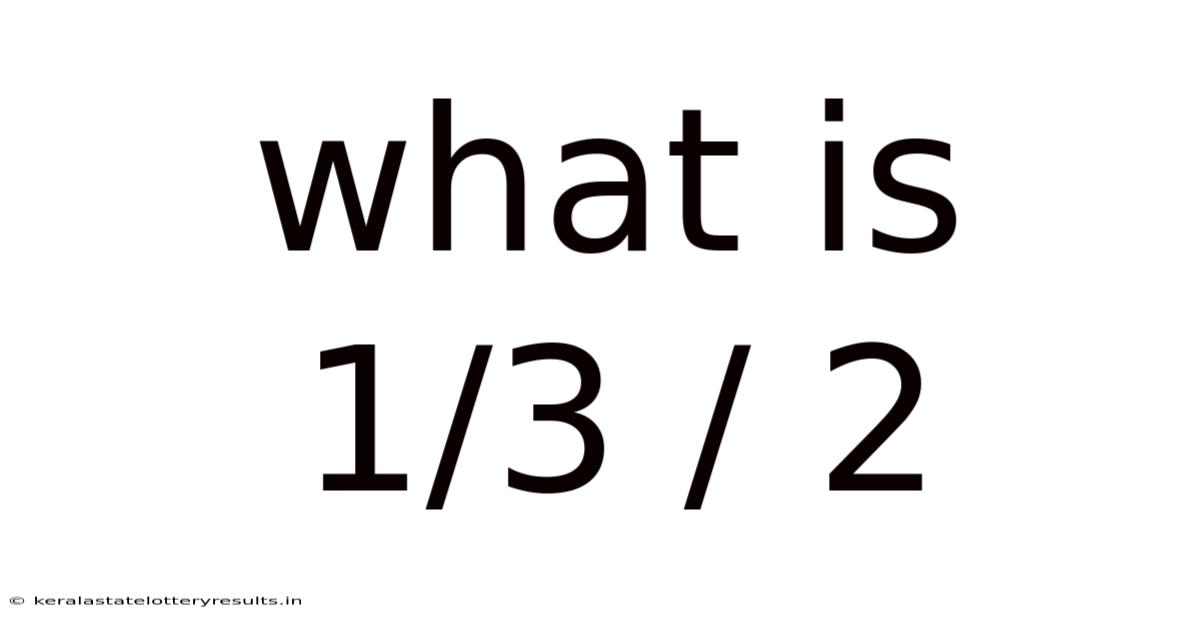
Table of Contents
Decoding 1/3 ÷ 2: A Deep Dive into Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a crucial skill in mathematics. This comprehensive guide will walk you through the process of solving 1/3 ÷ 2, explaining not only the how but also the why, providing a solid foundation for tackling more complex fraction problems. We'll explore different methods, delve into the underlying mathematical principles, and address frequently asked questions, ensuring a clear and complete understanding.
Introduction: Understanding the Basics of Fraction Division
Before diving into 1/3 ÷ 2, let's refresh our understanding of fraction division. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2. This principle forms the cornerstone of our approach to solving 1/3 ÷ 2. This seemingly simple problem introduces important concepts that are fundamental to higher-level math, including working with reciprocals, understanding the relationship between division and multiplication, and developing a solid intuitive grasp of fractions. Mastering these concepts will provide a firm foundation for future mathematical explorations.
Method 1: Using the Reciprocal
The most straightforward method to solve 1/3 ÷ 2 is by converting the whole number 2 into a fraction (2/1) and then using the reciprocal method. Here's how:
-
Rewrite the whole number as a fraction: The whole number 2 can be expressed as the fraction 2/1. This step is crucial because it allows us to apply the rules of fraction division consistently.
-
Find the reciprocal of the divisor: The divisor is 2/1. Its reciprocal is 1/2.
-
Change division to multiplication: Instead of dividing by 2/1, we multiply by its reciprocal, 1/2. This is the key step in fraction division: division by a fraction is equivalent to multiplication by its reciprocal.
-
Multiply the numerators and the denominators: Now, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together:
(1/3) ÷ (2/1) = (1/3) x (1/2) = (1 x 1) / (3 x 2) = 1/6
Therefore, 1/3 ÷ 2 = 1/6.
Method 2: Visualizing the Problem
A visual approach can significantly improve understanding, especially when dealing with fractions. Imagine you have a pizza cut into three equal slices. 1/3 represents one of these slices. Dividing this slice by 2 means splitting it into two equal parts. Each of these smaller parts represents 1/6 of the whole pizza. This visual representation directly corresponds to the mathematical result, providing an intuitive understanding of the process.
Method 3: Using Decimal Equivalents
While not always the preferred method for maintaining accuracy, converting fractions to decimals can provide an alternative approach.
-
Convert the fraction to a decimal: 1/3 expressed as a decimal is approximately 0.333... (a repeating decimal).
-
Divide the decimal by the whole number: Divide 0.333... by 2. This gives approximately 0.166...
-
Convert the decimal back to a fraction (if necessary): This step can be tricky with repeating decimals. In this case, 0.166... is approximately 1/6. This method is less precise than using the reciprocal method, especially when dealing with repeating decimals. The exact solution remains 1/6.
The Mathematical Principles Behind Fraction Division
The core principle behind fraction division lies in the inverse relationship between multiplication and division. When we divide by a number, we're essentially asking: "How many times does this number fit into the other?" When dividing fractions, the reciprocal helps us reframe this question in a way that's easier to calculate. Multiplying by the reciprocal essentially performs the division by finding the number of times the divisor fits into the dividend. This process is fundamentally rooted in the properties of multiplicative inverses.
Expanding the Concept: More Complex Fraction Division Problems
Understanding 1/3 ÷ 2 provides a solid base for tackling more complex fraction division problems. The same principles apply, even when dealing with fractions with larger numbers or mixed numbers (numbers with both whole and fractional parts). For example, let's consider the problem: (5/8) ÷ (3/4). Following the same steps:
-
Find the reciprocal of the divisor (3/4): The reciprocal is 4/3.
-
Change division to multiplication: (5/8) x (4/3)
-
Multiply the numerators and denominators: (5 x 4) / (8 x 3) = 20/24
-
Simplify the fraction: Both 20 and 24 are divisible by 4, simplifying the fraction to 5/6.
Therefore, (5/8) ÷ (3/4) = 5/6.
Frequently Asked Questions (FAQ)
-
Why do we use the reciprocal? Using the reciprocal transforms the division problem into a multiplication problem, making it much easier to calculate. It's based on the inverse relationship between multiplication and division.
-
What if the divisor is a mixed number? Convert the mixed number into an improper fraction (where the numerator is larger than the denominator) before applying the reciprocal method. For instance, 2 1/2 becomes 5/2.
-
Can I divide fractions using long division? While possible, it's generally less efficient than using the reciprocal method, particularly when dealing with complex fractions.
-
What happens if I divide by zero? Division by zero is undefined in mathematics. It's an operation that doesn't have a meaningful result.
-
How can I check my answer? You can check your answer by multiplying your result by the original divisor. If the result matches the original dividend, your answer is correct. For example, (1/6) x 2 = 1/3 which confirms that 1/6 is the correct answer to 1/3 ÷ 2.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial skill in mathematics. By understanding the underlying principles, and utilizing the reciprocal method, you can confidently tackle various fraction division problems, regardless of their complexity. Remember to practice regularly, and don't hesitate to use visual aids or different methods to deepen your understanding. The journey to mathematical proficiency is a continuous process of learning and refinement, and mastering fractions is a significant step along that path. The seemingly simple problem of 1/3 ÷ 2 has provided a gateway to understanding crucial concepts within the world of fractions and lays a strong foundation for more complex mathematical challenges. Remember to always break down complex problems into smaller, manageable steps, and the results will be both accurate and rewarding.
Latest Posts
Latest Posts
-
Lcm Of 2 And 5
Sep 16, 2025
-
22 Cm How Many Inches
Sep 16, 2025
-
X 4 X 5 2
Sep 16, 2025
-
Subtracting From A Negative Number
Sep 16, 2025
-
Is A Kite A Parallelogram
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 / 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.