What Is 20 Of 16
keralas
Sep 15, 2025 · 6 min read
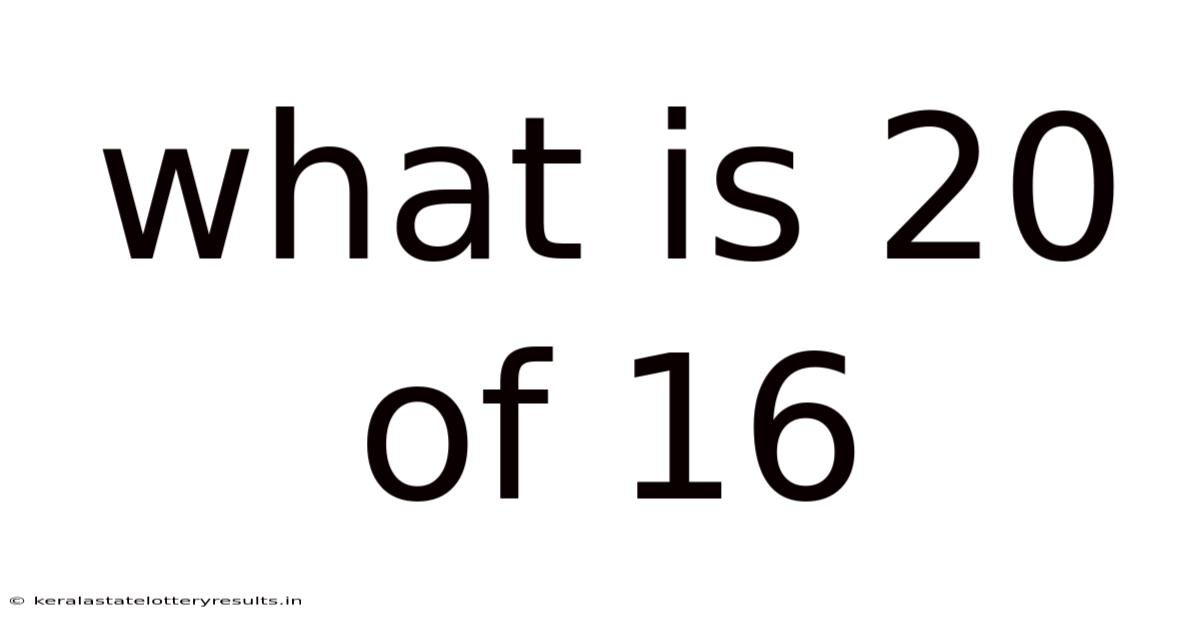
Table of Contents
What is 20 of 16? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 16?", opens a door to a fundamental understanding of mathematical concepts like fractions, percentages, and ratios. At first glance, it might seem illogical – how can you have 20 of something when you only have 16? However, this ambiguity highlights the importance of precise mathematical language and interpreting the question correctly. This article will explore various interpretations of this question, delve into the underlying mathematical principles, and provide a comprehensive explanation suitable for learners of all levels.
Understanding the Ambiguity: Different Interpretations
The phrase "20 of 16" is inherently ambiguous. It lacks the necessary mathematical operators to clearly define the intended operation. Let's consider several possible interpretations:
-
Interpretation 1: 20/16 as a Fraction: This is the most likely interpretation. It represents the fraction twenty-sixteenths (20/16). This fraction can be simplified, indicating a ratio or proportion.
-
Interpretation 2: 20% of 16: The phrase could be interpreted as "20 percent of 16." This represents a percentage calculation, finding a portion of a whole.
-
Interpretation 3: A Ratio: The phrase could represent a ratio of 20 to 16, expressing a relationship between two quantities.
We will explore each of these interpretations in detail.
Interpretation 1: 20/16 as a Fraction – Simplification and Decimal Representation
The simplest interpretation of "20 of 16" is the fraction 20/16. This fraction is improper because the numerator (20) is greater than the denominator (16). Improper fractions represent values greater than 1. To better understand its value, we simplify the fraction by finding the greatest common divisor (GCD) of 20 and 16.
The GCD of 20 and 16 is 4. Dividing both the numerator and the denominator by 4, we get:
20/16 = (20 ÷ 4) / (16 ÷ 4) = 5/4
This simplified fraction, 5/4, still represents an improper fraction. To convert it to a mixed number, we divide the numerator (5) by the denominator (4):
5 ÷ 4 = 1 with a remainder of 1
Therefore, 5/4 can be expressed as the mixed number 1 1/4. This means that 20 of 16 is equivalent to one and one-quarter.
We can also express this fraction as a decimal. Dividing 5 by 4, we get:
5 ÷ 4 = 1.25
Therefore, 20/16 is equal to 1.25.
Interpretation 2: 20% of 16 – Percentage Calculation
If "20 of 16" is interpreted as "20 percent of 16," we perform a percentage calculation. To find 20% of 16, we multiply 16 by 0.20 (which is the decimal equivalent of 20%):
16 x 0.20 = 3.2
Therefore, 20% of 16 is 3.2. This is a significantly different result compared to the fractional interpretation. This underscores the importance of clear mathematical notation and understanding the context of the problem.
Interpretation 3: 20 to 16 as a Ratio – Proportion and Scaling
The phrase "20 of 16" might also represent a ratio of 20 to 16. Ratios express the relative size of two or more quantities. Like fractions, ratios can be simplified. We find the GCD of 20 and 16 (which is 4), and simplify the ratio:
20:16 = (20 ÷ 4) : (16 ÷ 4) = 5:4
This simplified ratio, 5:4, indicates that for every 4 units of one quantity, there are 5 units of another. This ratio can be used for scaling or comparing proportions. For example, if a recipe calls for a 4:5 ratio of sugar to flour, and you want to increase the recipe, you could use the simplified ratio to maintain the correct proportion.
Ratios are fundamentally related to fractions. The ratio 5:4 is equivalent to the fraction 5/4.
The Importance of Mathematical Notation and Context
The ambiguity of "20 of 16" highlights the crucial role of precise mathematical notation. Without clear operators (such as +, -, ×, ÷, or %), the interpretation is open to multiple possibilities. The context in which this phrase appears is also critical. In a real-world problem, the context should provide sufficient clues to determine the intended operation.
For example, if the problem is related to sharing resources, the fractional interpretation might be more appropriate. If the problem involves discounts or percentages, the percentage interpretation is more likely.
Extending the Understanding: Further Exploration of Fractions, Percentages, and Ratios
This seemingly simple problem opens doors to a deeper exploration of several key mathematical concepts:
-
Fractions: Understanding fractions involves grasping the concepts of numerator, denominator, proper and improper fractions, simplification, and conversion to decimals and mixed numbers. This knowledge is essential for numerous mathematical applications.
-
Percentages: Percentages are a way of expressing a portion of a whole as a fraction of 100. Understanding percentage calculations is critical in various fields, including finance, statistics, and everyday life (e.g., calculating discounts, taxes, or tips).
-
Ratios: Ratios express the relative size of two or more quantities. They are often used to compare quantities, create proportions, and solve problems involving scaling or proportions. Ratios find application in fields such as cooking, engineering, and science.
-
Proportions: A proportion is a statement that two ratios are equal. Solving proportions is a common application involving ratios and fractions.
Frequently Asked Questions (FAQ)
Q: What is the most likely interpretation of "20 of 16"?
A: The most likely interpretation is 20/16, representing a fraction that can be simplified and converted to a decimal or mixed number.
Q: How do you simplify a fraction?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and divide both by the GCD.
Q: What is the difference between a proper and improper fraction?
A: A proper fraction has a numerator smaller than the denominator (e.g., 1/2). An improper fraction has a numerator greater than or equal to the denominator (e.g., 5/4).
Q: How do you convert a fraction to a decimal?
A: Divide the numerator by the denominator.
Q: How do you convert a fraction to a mixed number?
A: Divide the numerator by the denominator. The quotient is the whole number part of the mixed number. The remainder becomes the numerator of the fractional part, with the denominator remaining the same.
Conclusion
The question "What is 20 of 16?" is deceptively simple. Its ambiguity reveals the importance of precise mathematical language and context. By exploring different interpretations – as a fraction, a percentage, and a ratio – we've uncovered a rich understanding of foundational mathematical concepts. Mastering fractions, percentages, and ratios is essential for navigating various mathematical and real-world problems. This comprehensive analysis serves as a stepping stone to a deeper appreciation of these crucial building blocks of mathematics. Remember, clarity in mathematical expression is paramount for accurate and meaningful results.
Latest Posts
Latest Posts
-
L C M Of 3 And 6
Sep 15, 2025
-
13 Degrees Fahrenheit In Celsius
Sep 15, 2025
-
What Is 45 Of 20
Sep 15, 2025
-
1 4 1 4 Cup
Sep 15, 2025
-
Create Andanvec Graoh With Data
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.