What Is 2/3 Of 6
keralas
Sep 12, 2025 · 6 min read
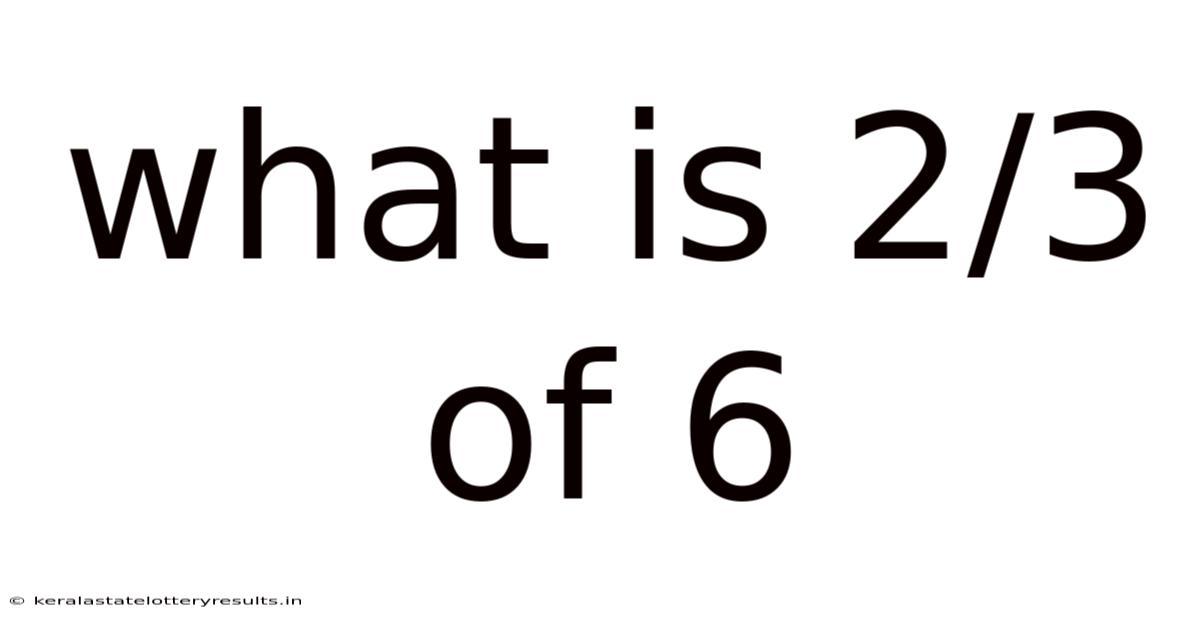
Table of Contents
What is 2/3 of 6? A Deep Dive into Fractions and Their Applications
Finding 2/3 of 6 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic calculation unlocks a gateway to a deeper understanding of fractions, their practical applications, and their importance in various fields. This article will not only provide the answer but also explore the underlying concepts, offer multiple solution methods, and delve into real-world examples where this type of calculation is crucial. This comprehensive guide aims to equip you with a strong grasp of fractions and their significance beyond simple arithmetic.
Understanding Fractions: A Foundation for Calculation
Before we tackle the problem of finding 2/3 of 6, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 2/3, 2 is the numerator and 3 is the denominator. This means we're considering 2 out of 3 equal parts.
Fractions are fundamental in various areas, including:
- Measurement: Expressing parts of units like inches, centimeters, or liters.
- Cooking & Baking: Following recipes that require precise ingredient measurements.
- Finance: Calculating percentages, discounts, and interest rates.
- Geometry: Determining proportions and ratios in shapes and figures.
- Probability: Representing the likelihood of an event occurring.
Mastering fractions is crucial for success in mathematics and its many real-world applications.
Multiple Approaches to Solving 2/3 of 6
Now, let's explore different ways to calculate 2/3 of 6. Each method offers a unique perspective on fractional calculations and reinforces the underlying concepts.
Method 1: Multiplication
The most direct way to find a fraction of a number is through multiplication. We can express "of" as multiplication. Therefore, 2/3 of 6 can be written as:
(2/3) * 6
To perform this multiplication, we can multiply the numerator (2) by 6 and then divide the result by the denominator (3):
(2 * 6) / 3 = 12 / 3 = 4
Therefore, 2/3 of 6 is 4.
Method 2: Division and Multiplication
Another approach involves first dividing the whole number (6) by the denominator (3) and then multiplying the result by the numerator (2):
6 / 3 = 2 2 * 2 = 4
This method highlights the idea of dividing the whole into equal parts and then selecting the desired number of parts. It emphasizes the meaning of the denominator as the number of equal parts.
Method 3: Visual Representation
Visual aids can be incredibly helpful in understanding fractions. Imagine a rectangle divided into three equal parts. Each part represents 1/3 of the whole. If we shade two of these parts, we represent 2/3. Since the whole rectangle represents 6, each part represents 6/3 = 2. Therefore, the shaded area (2/3) represents 2 * 2 = 4.
This method is particularly useful for beginners and visually strengthens the conceptual understanding of fractions.
Extending the Understanding: Working with Different Fractions and Numbers
Let's apply the methods we've learned to calculate other fractions of different numbers. This will reinforce our understanding and demonstrate the versatility of these techniques.
Example 1: Finding 3/4 of 12
Using the multiplication method:
(3/4) * 12 = (3 * 12) / 4 = 36 / 4 = 9
Therefore, 3/4 of 12 is 9.
Example 2: Finding 1/5 of 20
Using the division and multiplication method:
20 / 5 = 4 4 * 1 = 4
Therefore, 1/5 of 20 is 4.
Example 3: Finding 5/8 of 24
Using the multiplication method:
(5/8) * 24 = (5 * 24) / 8 = 120 / 8 = 15
Therefore, 5/8 of 24 is 15.
Real-World Applications: Where Fractions Matter
The seemingly simple calculation of 2/3 of 6 finds applications in various real-world scenarios. Here are a few examples:
- Sharing Resources: Imagine you have 6 cookies to share among 3 friends. If you want to give each friend 2/3 of the cookies, each friend receives 2/3 * 6 = 4 cookies.
- Recipe Scaling: A recipe calls for 6 cups of flour, and you only want to make 2/3 of the recipe. You would need 2/3 * 6 = 4 cups of flour.
- Discount Calculations: A store offers a 2/3 discount on an item priced at $6. The discount amount is 2/3 * $6 = $4.
- Geometry Problems: If a rectangle has an area of 6 square units, and you need to find the area of a section that's 2/3 of the rectangle, the area of that section is 2/3 * 6 = 4 square units.
- Probability: If the probability of an event is 2/3, and there are 6 possible outcomes, the number of favorable outcomes is 2/3 * 6 = 4.
Beyond the Basics: Improper Fractions and Mixed Numbers
So far, we've focused on proper fractions (where the numerator is smaller than the denominator). However, we can also encounter improper fractions (where the numerator is greater than or equal to the denominator) and mixed numbers (a combination of a whole number and a fraction). Let's extend our understanding to include these.
Improper Fractions: An improper fraction like 7/3 represents more than one whole. To solve problems involving improper fractions, you can convert them to mixed numbers or directly perform the calculations.
Mixed Numbers: A mixed number like 2 1/3 combines a whole number (2) and a fraction (1/3). To perform calculations with mixed numbers, it's usually best to convert them to improper fractions first. For example, 2 1/3 can be converted to (2 * 3 + 1) / 3 = 7/3.
Let's consider an example: Finding 5/2 of 8
5/2 * 8 = 40/2 = 20
Or converting 5/2 to a mixed number: 2 1/2. Then 2 1/2 * 8 = 16 + 4 = 20.
Frequently Asked Questions (FAQ)
Q1: What if I have a fraction where the numerator is larger than the denominator?
A1: This is an improper fraction, representing more than one whole. You can solve this by converting the improper fraction to a mixed number (a whole number and a fraction) or by directly performing the multiplication.
Q2: Can I use a calculator to find a fraction of a number?
A2: Yes, you can use a calculator. Simply input the fraction as a decimal (for example, 2/3 as 0.666...) and multiply by the number.
Q3: How do I find a fraction of a decimal number?
A3: Convert the decimal to a fraction first and then proceed with the calculation as you would with a fraction and a whole number.
Q4: Are there any online tools to help me practice fractions?
A4: Yes, many educational websites and apps offer interactive exercises and games to help you practice working with fractions.
Conclusion: Mastering Fractions – A Journey Beyond the Basics
The seemingly simple problem of finding 2/3 of 6 opens the door to a rich understanding of fractions and their diverse applications. This article has explored various methods for solving such problems, extended the understanding to include improper fractions and mixed numbers, and highlighted the relevance of these concepts in various real-world scenarios. By grasping the fundamentals of fractions, you build a solid foundation for success in mathematics and related fields. Remember, understanding fractions is not just about memorizing formulas, it's about developing a deep, intuitive understanding of parts and wholes, a skill that will continue to serve you well throughout your life.
Latest Posts
Latest Posts
-
X 2 X 1 1
Sep 12, 2025
-
Whats 20 Percent Of 40
Sep 12, 2025
-
Convert 43 Celsius To Fahrenheit
Sep 12, 2025
-
How Many Feet Is 71
Sep 12, 2025
-
How Long Is 10 Minutes
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Of 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.