What Is 2 3 8
keralas
Sep 17, 2025 · 5 min read
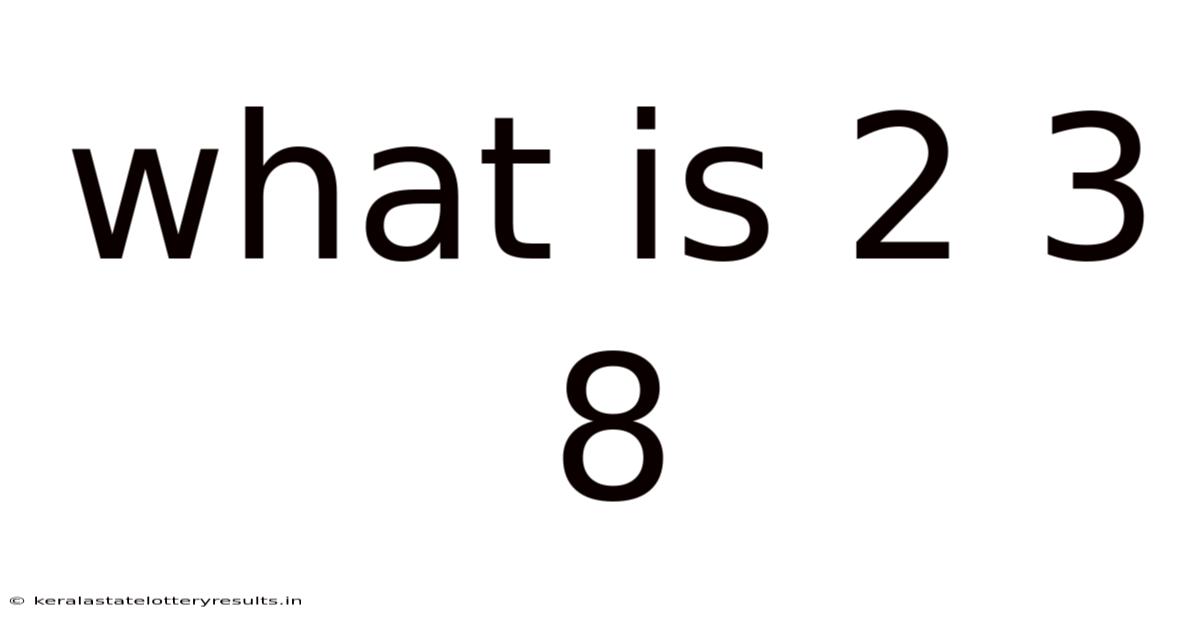
Table of Contents
Decoding the Mystery: What is 2 3 8? A Deep Dive into Number Sequences and Their Significance
The seemingly simple sequence "2 3 8" might initially appear insignificant. However, depending on the context, it can represent a multitude of things, from a simple numerical progression to a complex code, a mathematical puzzle, or even a significant date. This article will explore the various interpretations of "2 3 8," delve into the mathematical concepts surrounding number sequences, and unravel the potential meanings behind this specific sequence. We'll examine possibilities ranging from straightforward arithmetic progressions to more intricate patterns and their applications in different fields.
Understanding Number Sequences: A Foundation
Before we delve into the specifics of "2 3 8," it's essential to understand the broader context of number sequences. Number sequences are ordered sets of numbers that often follow a specific pattern or rule. These patterns can be simple, like an arithmetic progression (where each number is obtained by adding a constant value to the previous one), or significantly more complex, involving geometric progressions, Fibonacci sequences, or even chaotic systems.
Types of Number Sequences:
- Arithmetic Progression: A sequence where the difference between consecutive terms remains constant. Example: 2, 5, 8, 11, 14... (common difference = 3)
- Geometric Progression: A sequence where each term is obtained by multiplying the previous term by a constant value. Example: 2, 6, 18, 54... (common ratio = 3)
- Fibonacci Sequence: A sequence where each term is the sum of the two preceding terms. Example: 1, 1, 2, 3, 5, 8, 13...
- Geometric-Arithmetic Sequence: A sequence that combines aspects of both geometric and arithmetic progressions.
- Recursive Sequences: Sequences where each term is defined by a formula involving previous terms.
Identifying the underlying pattern in a number sequence is a fundamental skill in mathematics, with applications ranging from cryptography to financial modeling. The ability to recognize these patterns allows for predictions, extrapolations, and the understanding of complex systems.
Exploring Potential Interpretations of "2 3 8"
Now, let's return to the sequence "2 3 8." Without additional context, its interpretation is inherently ambiguous. However, we can explore several potential meanings:
1. A Simple Sequence (Lacking an Obvious Pattern):
The most straightforward interpretation is that "2 3 8" is simply a short, arbitrary sequence of numbers without a discernible mathematical pattern. It could represent anything from a random selection to a code with a yet-undisclosed key. Without further information, this remains a valid, albeit uninformative, possibility.
2. A Truncated Sequence (Part of a Larger Pattern):
It's possible that "2 3 8" is a fragment of a larger, more structured sequence. To understand its true nature, we would need additional numbers to identify the underlying rule. For example, it could be:
- Part of an Arithmetic Progression: If the differences between consecutive terms are consistently increasing or decreasing, we could potentially extrapolate. However, with only three terms, this is difficult to ascertain definitively.
- Part of a Geometric Progression: Similarly, a geometric progression is unlikely without further data.
- Part of a More Complex Sequence: The sequence might adhere to a non-linear, recursive, or otherwise intricate rule that requires more terms to decipher.
3. A Code or Cipher:
"2 3 8" could be part of a code or cipher. In cryptography, numerical sequences are often used to represent letters, words, or concepts. The meaning would entirely depend on the chosen encoding scheme. This requires a key or further context to decrypt.
4. A Date or Reference Number:
The sequence could represent a date (perhaps in a specific format) or a reference number in a specific system. Again, this necessitates further context. For instance, it could be a short code used in a database, inventory management system, or other data-driven application.
5. Mathematical Puzzle or Problem:
The sequence could form part of a larger mathematical puzzle or problem. The solution could involve finding a hidden pattern, solving an equation, or applying a specific mathematical operation to reveal a hidden meaning. Without specific instructions or a related problem, however, this remains speculative.
The Importance of Context in Interpreting Number Sequences
As demonstrated, the interpretation of "2 3 8" is heavily reliant on context. Without additional information or clues, its meaning remains ambiguous. This highlights the crucial role of context in deciphering numerical sequences and interpreting data in general. Consider these points:
- Source of the Sequence: Where did this sequence originate? A scientific experiment? A piece of code? A mathematical problem? The source provides vital clues about its potential meaning.
- Surrounding Information: What other data accompanies the sequence? Are there any accompanying instructions, descriptions, or related numbers? These details often provide critical context.
- Intended Audience: Who is the intended recipient of this sequence? Understanding the audience can help narrow down the potential interpretations.
Advanced Considerations: Applications in Various Fields
Number sequences play a significant role in various fields. Let's briefly explore some examples:
1. Cryptography: Secure communication relies heavily on complex number sequences and patterns. Cryptography uses sophisticated algorithms to encrypt and decrypt messages, often involving prime numbers, modular arithmetic, and other advanced mathematical concepts.
2. Financial Modeling: Predictive models in finance often utilize time series analysis, which involves identifying patterns and trends in sequences of financial data (e.g., stock prices, interest rates). These patterns inform investment decisions and risk assessment.
3. Computer Science: Algorithms and data structures often rely on numerical sequences. For instance, sorting algorithms may utilize specific sequences to optimize their performance. Furthermore, many computer programs involve iterations, and these iterations often follow a structured numerical progression.
4. Physics and Engineering: Many physical phenomena can be modeled using mathematical sequences. For example, the behavior of oscillating systems, radioactive decay, and population dynamics can often be described using specific types of number sequences.
Conclusion: The Elusive Nature of Meaning
The seemingly simple sequence "2 3 8" serves as a compelling example of how context shapes meaning. Without additional information, the possibilities are virtually limitless. It could be a random sequence, part of a larger pattern, a code, a date, or a component of a more complex mathematical puzzle. This ambiguity underscores the importance of considering the context when interpreting numerical data. The more context you have, the more accurately you can decipher the meaning of the sequence and understand its implications. Furthermore, the exploration of number sequences demonstrates the power of mathematical patterns and their profound applications across numerous scientific and technological domains.
Latest Posts
Latest Posts
-
5 16 In Decimal Form
Sep 17, 2025
-
What The Factors Of 64
Sep 17, 2025
-
How To Divide Binary Numbers
Sep 17, 2025
-
How Are Unlike Fractions Identified
Sep 17, 2025
-
What Is Xxiv In Numbers
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.