X 4 X 5 2
keralas
Sep 16, 2025 · 6 min read
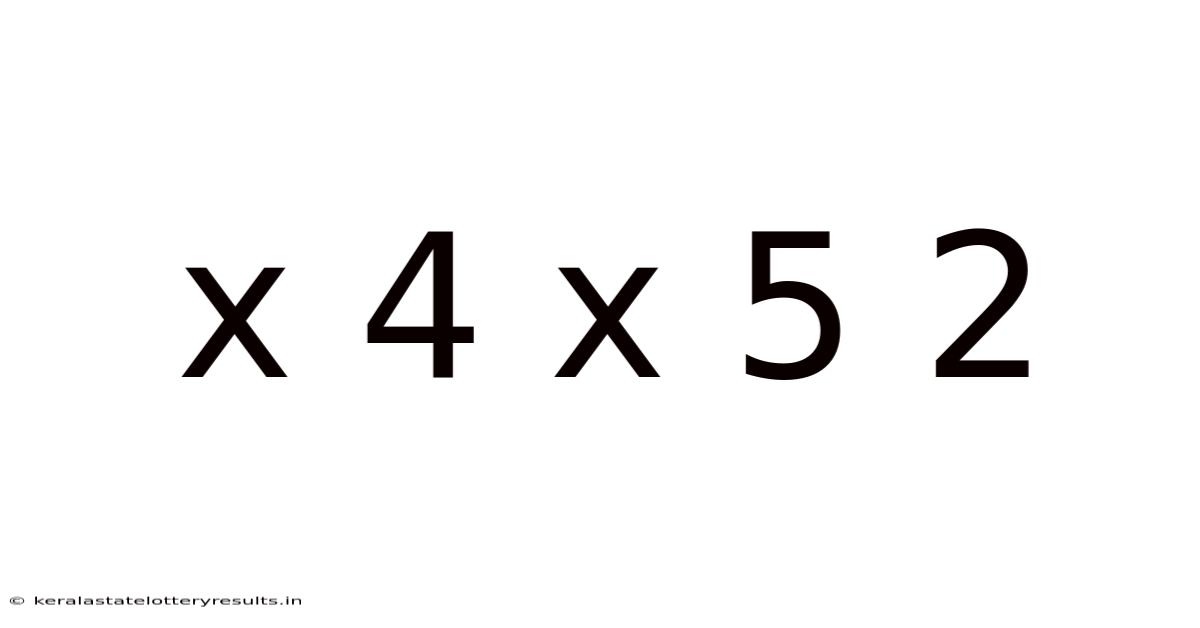
Table of Contents
Decoding the Mystery of "x 4 x 5 2": Exploring Mathematical Expressions and Problem-Solving Strategies
The seemingly simple expression "x 4 x 5 2" presents a fascinating challenge, highlighting the importance of order of operations in mathematics. This article will delve deep into understanding this expression, exploring different interpretations, the crucial role of the order of operations (often remembered by the acronym PEMDAS/BODMAS), and various problem-solving strategies applicable to similar mathematical puzzles. We will also examine the broader context of mathematical notation and how seemingly ambiguous expressions can be clarified through precise and consistent application of mathematical rules.
Understanding the Ambiguity: Why Order of Operations Matters
The primary challenge with "x 4 x 5 2" lies in its ambiguous nature. Without explicitly defined parentheses or other grouping symbols, the order in which the operations are performed significantly impacts the final result. This ambiguity underscores the critical importance of the order of operations, a set of rules that dictates the sequence in which mathematical operations should be carried out.
The commonly used acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) and BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction) represent the same fundamental principles. Both emphasize that calculations within parentheses or brackets should be done first, followed by exponents or orders (like square roots), then multiplication and division (from left to right), and finally addition and subtraction (also from left to right).
Let's consider different interpretations of "x 4 x 5 2" based on varying orders of operations:
Scenario 1: Left-to-Right Interpretation (Incorrect)
If we were to simply proceed from left to right without considering the order of operations, we would have:
x 4 = 4x 4x x 5 = 20x 20x 2 = 20x - 2 (assuming subtraction, though it could also be interpreted as 20x/2)
This approach is incorrect because it neglects the established order of operations. It highlights the potential for significant errors if the established rules are not followed consistently.
Scenario 2: Correct Interpretation Using PEMDAS/BODMAS
Since there are no parentheses or exponents in "x 4 x 5 2," we proceed to multiplication and division from left to right:
- Step 1: x 4 This results in 4x.
- Step 2: 4x x 5 This results in 20x.
- Step 3: 20x 2 This is where interpretation becomes crucial. If '2' is meant to be a subtraction, we get 20x - 2. If '2' is meant to be a division we get 10x.
Therefore, depending on the intended operation between 20x and 2, the correct answer is either 20x - 2 or 10x. The ambiguity underscores the need for clearer notation in mathematical expressions.
Clarifying the Expression: The Power of Parentheses
To eliminate the ambiguity and ensure a single, unambiguous answer, we should rewrite the expression using parentheses. For instance:
-
(x * 4) * (5 - 2): This expression clearly indicates that we should first perform the subtraction (5 - 2 = 3), then the multiplications: (x * 4) * 3 = 12x. This clarifies the intended order of operations.
-
(x * 4 * 5) / 2: This expression implies multiplying x, 4, and 5 first, then dividing the result by 2. The result would be (20x)/2 = 10x
-
(x * 4) * 5 - 2: This expression clarifies the operations are performed left to right, resulting in 20x - 2
-
x * (4 * 5) -2: This expression would give 20x - 2
By strategically using parentheses, we can precisely specify the intended order of operations, leading to a single, unambiguous result. This highlights the crucial role of clear and precise mathematical notation in avoiding errors and ensuring effective communication of mathematical concepts.
Expanding the Scope: Beyond Simple Arithmetic
The principles illustrated through analyzing "x 4 x 5 2" extend far beyond simple arithmetic. These principles are foundational to more complex mathematical concepts and calculations:
-
Algebra: In algebraic expressions, the order of operations is critical for solving equations and simplifying expressions. Incorrect application of the order of operations can lead to inaccurate solutions.
-
Calculus: Calculus relies heavily on the correct order of operations in evaluating limits, derivatives, and integrals. Misapplication can lead to significant errors in calculations.
-
Computer Programming: Programming languages strictly adhere to the order of operations. Understanding these rules is essential for writing correct and efficient computer programs. Incorrect ordering can lead to unexpected results and program errors.
-
Data Analysis: In data analysis, particularly when working with formulas and calculations, the correct order of operations is paramount for accurate results.
Frequently Asked Questions (FAQ)
-
Q: What is the most important thing to remember when evaluating expressions like "x 4 x 5 2"?
- A: The most important thing is to remember and correctly apply the order of operations (PEMDAS/BODMAS). This ensures that the operations are performed in the correct sequence, leading to an accurate result. Ambiguity can be easily avoided by using parentheses to clarify the intended order.
-
Q: Why is using parentheses important?
- A: Parentheses explicitly indicate the order in which operations should be performed, eliminating ambiguity and preventing misinterpretations. This ensures that everyone understands and interprets the expression in the same way, leading to consistent results.
-
Q: Can I solve this without knowing the value of 'x'?
- A: Yes. You can simplify the expression using the order of operations, even without knowing the specific numerical value of 'x'. The result will still be an algebraic expression involving 'x'.
-
Q: What happens if there's a mix of multiplication and division in an expression?
- A: In the absence of parentheses, perform multiplication and division from left to right, in the order they appear in the expression.
-
Q: What if I see a similar problem, but with different operations (like addition or subtraction)?
- A: The same fundamental principles of PEMDAS/BODMAS still apply. Always handle parentheses and exponents first, then multiplication and division (left to right), and finally addition and subtraction (left to right).
Conclusion: Mastering Mathematical Precision
The seemingly simple expression "x 4 x 5 2" serves as a powerful reminder of the importance of precision and clarity in mathematics. The order of operations is not a mere set of arbitrary rules; it's a fundamental framework ensuring that mathematical expressions are interpreted and evaluated consistently. By mastering the order of operations and using parentheses effectively, we can avoid ambiguity, ensure accuracy in calculations, and confidently tackle more complex mathematical problems. Understanding these principles is essential for success in various fields that rely on mathematical precision and accuracy, from basic arithmetic to advanced scientific and technological applications. The key takeaway is to embrace clear notation and consistent application of the order of operations to prevent misinterpretations and ensure accurate solutions.
Latest Posts
Latest Posts
-
Decimal To Fraction Table Chart
Sep 16, 2025
-
Simple Interest Versus Compound Interest
Sep 16, 2025
-
What Is A 9 15 Grade
Sep 16, 2025
-
Tangent To A Circle Formula
Sep 16, 2025
-
16 Oz To A Quart
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X 4 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.