Symbol For Not Equal To
keralas
Sep 16, 2025 · 6 min read
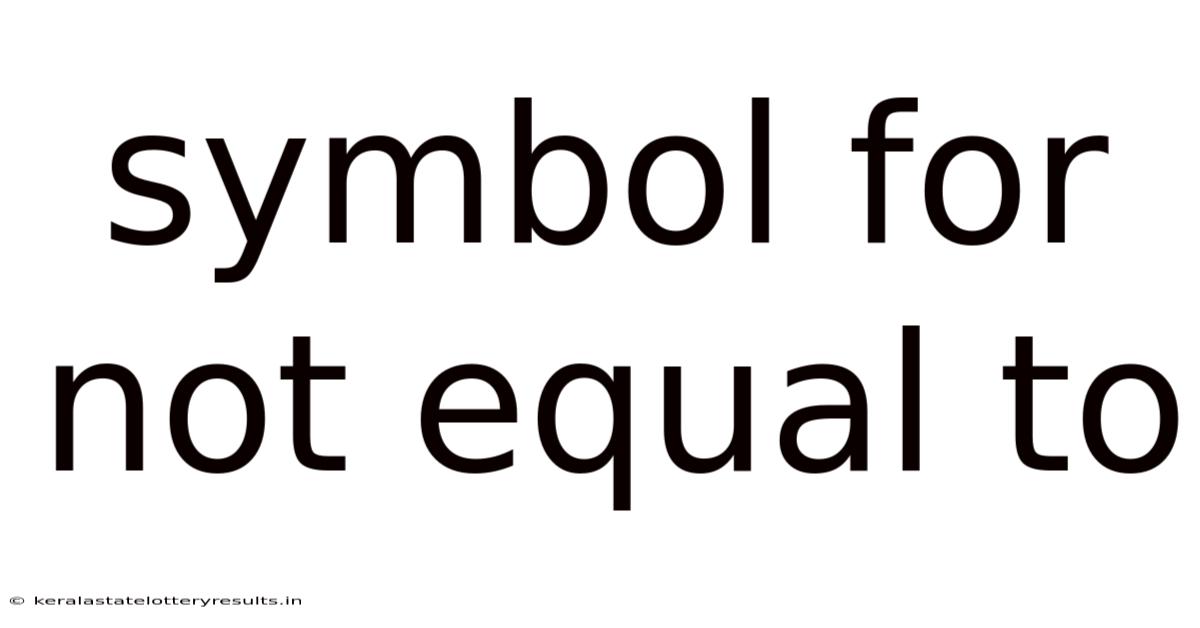
Table of Contents
The Symbol for "Not Equal To": A Deep Dive into ≠ and its Mathematical Significance
The symbol ≠, representing "not equal to," is a fundamental element in mathematics and logic. While seemingly simple, its implications are far-reaching, impacting various fields from basic arithmetic to advanced calculus and computer science. This comprehensive guide will explore the symbol's origins, its usage across different mathematical contexts, its relationship to other inequality symbols, and its importance in problem-solving and logical reasoning. We'll also delve into common misconceptions and frequently asked questions to ensure a complete understanding of this crucial mathematical notation.
Understanding the ≠ Symbol: Origins and Evolution
The "not equal to" symbol, ≠, is a direct negation of the "equals" symbol, =. The equals sign itself has a rich history, with its modern form attributed to Robert Recorde in 1557. He argued that two parallel lines of equal length were the most fitting representation of equality. The negation of this, the crossed-out equals sign, naturally followed as the logical representation of inequality. While the precise timeline of its adoption is difficult to pinpoint, its widespread use solidified over centuries as mathematical notation standardized. Its simplicity and intuitive design made it universally accepted, ensuring clear and unambiguous communication in mathematical expressions.
Using ≠ in Different Mathematical Contexts
The ≠ symbol finds application across a broad spectrum of mathematical concepts. Let's explore some key areas:
1. Basic Arithmetic and Algebra:
At its most basic level, ≠ signifies that two numerical values or algebraic expressions are not identical. For example:
- 5 ≠ 7 (Five is not equal to seven)
- x + 2 ≠ 10 (The value of 'x' plus 2 is not equal to 10)
- (2 + 3) ≠ (2 x 3) (The sum of 2 and 3 is not equal to the product of 2 and 3)
The symbol is crucial in solving equations and inequalities. When solving an equation, we aim to find values that make the equation true (using =). Conversely, using ≠ helps identify values that make the equation false.
2. Set Theory:
In set theory, ≠ is used to indicate that two sets do not contain the same elements. Sets are collections of objects, and two sets are considered equal only if they have precisely the same members, regardless of order.
- {1, 2, 3} ≠ {3, 2, 1} (Both sets contain the same elements, but their order differs. In set theory, order doesn't matter for equality).
- {a, b, c} ≠ {a, b, d} (These sets have different elements and are therefore not equal.)
- A ≠ Ø (Set A is not equal to the empty set)
The use of ≠ in set theory is fundamental to understanding set relationships, subsets, and operations such as unions and intersections.
3. Geometry and Trigonometry:
The "not equal to" symbol plays a critical role in geometric proofs and trigonometric identities. It helps establish conditions where geometric figures or trigonometric expressions are not congruent, similar, or equivalent.
- Two triangles are not congruent if their corresponding sides and angles are not equal.
- Two angles are not equal in measure unless specific conditions are met.
- A trigonometric identity is proven by showing that two expressions are equal for all valid inputs, otherwise they would be represented as not equal (≠).
4. Calculus and Analysis:
In advanced mathematical fields like calculus and real analysis, the symbol ≠ is used to define limits, derivatives, and integrals more precisely. It helps specify conditions under which functions are not continuous, differentiable, or integrable.
- A function is discontinuous at a point x if the limit of the function as x approaches that point is not equal to the function's value at that point.
- The derivative of a function does not exist at points where the function is not differentiable.
5. Logic and Boolean Algebra:
The "not equal to" symbol extends its utility into logic and Boolean algebra. It represents logical inequality, indicating that two logical statements or Boolean expressions are not equivalent. In programming, this symbol is crucial in conditional statements and comparisons.
- A ≠ B (Logical statement A is not equivalent to logical statement B)
- x ≠ y (Boolean variable x is not equal to Boolean variable y)
Relationship to Other Inequality Symbols
The ≠ symbol is part of a larger family of inequality symbols that express different relationships between values. It is essential to understand the nuances between them:
- < (Less than): Indicates that one value is strictly smaller than another. For example, 3 < 5.
- > (Greater than): Indicates that one value is strictly larger than another. For example, 5 > 3.
- ≤ (Less than or equal to): Indicates that one value is either smaller than or equal to another. For example, 3 ≤ 3 and 3 ≤ 5.
- ≥ (Greater than or equal to): Indicates that one value is either larger than or equal to another. For example, 5 ≥ 5 and 5 ≥ 3.
Understanding these symbols and their differences is critical for correctly expressing and interpreting mathematical relationships. The ≠ symbol sits in contrast to both the equality (=) and the other inequality symbols.
Problem-Solving with ≠
The "not equal to" symbol is fundamental in solving various mathematical problems. Let's examine a few examples:
Example 1: Finding solutions that do not satisfy an equation.
Consider the equation 2x + 1 = 7. Solving this yields x = 3. Any other value of x will make the equation untrue. We can express this using ≠:
2x + 1 ≠ 7 when x ≠ 3
Example 2: Determining domain restrictions.
In functions, the ≠ symbol is used to exclude values from the domain that would lead to undefined results (e.g., division by zero).
Consider the function f(x) = 1/x. The denominator cannot be zero, so the domain restriction is x ≠ 0.
Example 3: Solving inequalities.
Solving inequalities often involves using ≠ to exclude values that do not satisfy the given condition.
For example, solving x + 2 > 5 leads to x > 3. This implicitly means that x ≠ 3 and x ≠ any value less than 3.
Frequently Asked Questions (FAQ)
Q1: What is the difference between ≠ and < or >?
A1: The symbols < and > denote strict inequalities (one value is definitively smaller or larger), while ≠ simply indicates that two values are different without specifying which is larger or smaller. For example, 2 ≠ 5 encompasses both 2 < 5 and 2 > 5, whereas only one would be true when using < or > alone.
Q2: Can ≠ be used with complex numbers?
A2: Yes, the "not equal to" symbol applies to complex numbers as well. Two complex numbers are unequal if their real or imaginary parts (or both) are different.
Q3: Is there a specific Unicode character for ≠?
A3: Yes, the Unicode character for ≠ is U+2260. This ensures consistent representation across different systems and software.
Q4: How is ≠ used in programming?
A4: In most programming languages, ≠ is represented by "!=". This operator is used in conditional statements to check if two values are not equal. For instance, if (x != y) { ... } executes the code block only if x and y are different.
Q5: Can ≠ be used in formal mathematical proofs?
A5: Absolutely. The ≠ symbol is a standard mathematical notation and is perfectly acceptable in formal proofs to denote inequality or to demonstrate a contradiction.
Conclusion: The Unsung Hero of Mathematical Communication
The seemingly simple "not equal to" symbol (≠) plays a surprisingly significant role in mathematics. Its applications extend far beyond elementary arithmetic, impacting various mathematical branches and computational fields. Understanding its meaning, usage, and relationship to other inequality symbols is vital for anyone pursuing mathematical studies or working with quantitative data. Its ability to clearly and concisely convey non-equality is an essential component of mathematical precision and effective communication, ensuring clarity and preventing ambiguity in complex calculations and logical reasoning. While often overlooked, its presence is a constant reminder of the importance of precise notation in the intricate world of mathematics.
Latest Posts
Latest Posts
-
90 Degrees Celsius To Fahrenheit
Sep 16, 2025
-
Gcf Of 42 And 24
Sep 16, 2025
-
Rearrange Expression Into Quadratic Form
Sep 16, 2025
-
Gcf Of 30 And 16
Sep 16, 2025
-
What Is 100 Of 15
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Symbol For Not Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.