Solve 4x 2 25 0
keralas
Sep 17, 2025 · 6 min read
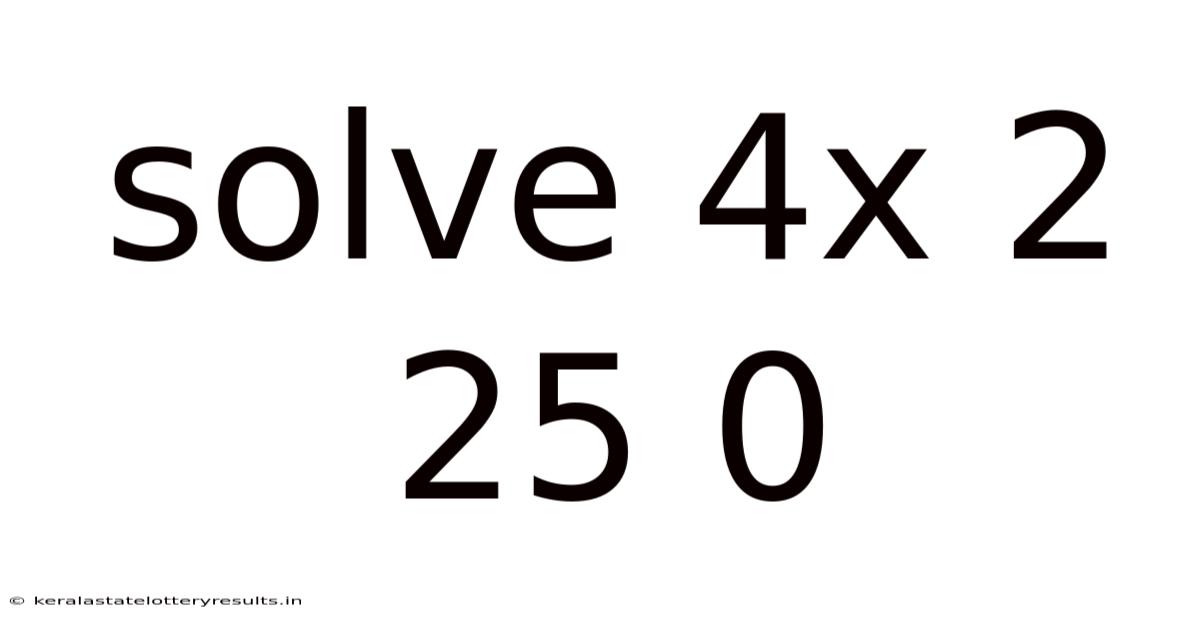
Table of Contents
Solving the Quadratic Equation 4x² + 25 = 0: A Comprehensive Guide
This article provides a comprehensive guide on how to solve the quadratic equation 4x² + 25 = 0. We'll explore various methods, delve into the underlying mathematical concepts, and address common misconceptions. Understanding how to solve quadratic equations is fundamental in algebra and has widespread applications in various fields, from physics and engineering to finance and computer science. This guide is designed for students of all levels, from beginners needing a solid foundation to those looking for a deeper understanding of the process.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our specific equation, 4x² + 25 = 0, is a slightly simpler form as the 'b' coefficient is zero.
This particular equation presents a unique challenge because it lacks a linear term (the 'bx' term). This simplification, however, doesn't make it less important; understanding how to solve it is crucial for grasping the broader concepts of quadratic equations and their solutions.
Method 1: Isolating the Variable (Solving for x)
The most straightforward approach to solving 4x² + 25 = 0 is by isolating the variable 'x'. Let's follow these steps:
-
Subtract 25 from both sides: This step aims to isolate the term containing 'x'. Subtracting 25 from both sides gives us: 4x² = -25
-
Divide both sides by 4: This step further isolates x². Dividing both sides by 4 yields: x² = -25/4
-
Take the square root of both sides: Remember that taking the square root introduces both a positive and a negative solution. This is because both (+5)² and (-5)² equal 25. Therefore: x = ±√(-25/4)
-
Simplify the square root: Notice that we have a negative number under the square root. This indicates that the solutions will be complex numbers. We can simplify this expression as follows: x = ±(√25/√4) * √(-1) x = ±(5/2)i
Where 'i' represents the imaginary unit, defined as √(-1).
Therefore, the solutions to the equation 4x² + 25 = 0 are x = (5/2)i and x = -(5/2)i.
Method 2: Using the Quadratic Formula
The quadratic formula is a powerful tool for solving any quadratic equation, regardless of the values of 'a', 'b', and 'c'. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
In our equation, 4x² + 25 = 0, we have: a = 4, b = 0, and c = 25. Substituting these values into the quadratic formula:
x = [-0 ± √(0² - 4 * 4 * 25)] / (2 * 4) x = ± √(-400) / 8 x = ± √(400 * -1) / 8 x = ± (20i) / 8 x = ± (5/2)i
This method confirms the same solutions obtained through the previous method: x = (5/2)i and x = -(5/2)i.
Understanding Complex Numbers
The solutions we've obtained, (5/2)i and -(5/2)i, are complex numbers. A complex number has two parts: a real part and an imaginary part. In our case, the real part is 0, and the imaginary part is ±(5/2).
Complex numbers are crucial in various areas of mathematics, physics, and engineering. They extend the number system beyond real numbers, allowing us to solve equations that wouldn't have solutions within the realm of real numbers alone.
Graphical Representation: The Complex Plane
While we can't directly graph complex solutions on a standard Cartesian coordinate system (x-y plane), we can represent them on a complex plane. The complex plane has a real axis (horizontal) and an imaginary axis (vertical). The complex number (5/2)i would be represented as a point 5/2 units above the origin (0,0) on the imaginary axis. Similarly, -(5/2)i would be 5/2 units below the origin.
Method 3: Factoring (Not Applicable in this Case)
Factoring is a method used to solve quadratic equations by expressing the quadratic expression as a product of two linear expressions. However, factoring is not directly applicable to the equation 4x² + 25 = 0 because it doesn't factor nicely using real numbers. The lack of a linear term makes it impossible to find two numbers that add up to zero (the 'b' coefficient) and multiply to 100 (4*25). The solution requires the use of complex numbers, making the previous methods more appropriate.
The Discriminant: Predicting the Nature of Roots
The discriminant (Δ or D), given by b² - 4ac, plays a critical role in determining the nature of the roots (solutions) of a quadratic equation.
- Δ > 0: The equation has two distinct real roots.
- Δ = 0: The equation has one real root (a repeated root).
- Δ < 0: The equation has two complex conjugate roots (as in our case).
In our equation, 4x² + 25 = 0, the discriminant is:
Δ = 0² - 4 * 4 * 25 = -400
Since the discriminant is negative, we correctly predicted that the equation has two complex conjugate roots. Complex conjugate roots always appear in pairs, with one being the negative of the other.
Applications of Quadratic Equations
Quadratic equations and their solutions find applications in many areas:
- Physics: Projectile motion, calculating the trajectory of objects under gravity.
- Engineering: Designing structures, analyzing circuits, and modeling various physical phenomena.
- Finance: Calculating compound interest, determining optimal investment strategies.
- Computer Graphics: Creating curves and shapes, modeling 3D objects.
Frequently Asked Questions (FAQ)
Q1: Why are complex numbers necessary to solve this equation?
A1: Because the discriminant is negative, indicating that the parabola represented by the quadratic equation doesn't intersect the x-axis in the real number plane. Complex numbers extend the number system to encompass solutions that lie outside the real number line.
Q2: Can I use a calculator to solve this equation?
A2: Yes, many scientific calculators can handle complex numbers and solve quadratic equations directly. However, understanding the underlying mathematical concepts is crucial for applying these tools effectively and interpreting the results correctly.
Q3: What is the significance of complex conjugate roots?
A3: Complex conjugate roots often appear in systems that exhibit oscillation or damping. In electrical engineering, for instance, they represent the resonant frequencies of circuits.
Q4: Are there other ways to solve quadratic equations?
A4: Yes, besides the methods discussed here, other techniques include completing the square and graphical methods. The best approach often depends on the specific equation and the context in which it arises.
Conclusion: Mastering Quadratic Equations
Solving the equation 4x² + 25 = 0 involves understanding the nature of quadratic equations, utilizing appropriate solution methods, and interpreting the results within the context of complex numbers. This seemingly simple equation provides a valuable opportunity to grasp fundamental algebraic concepts and their broader applications. Through mastering this type of problem, you build a strong foundation for tackling more complex mathematical challenges in various fields of study and professional endeavors. Remember that practice is key – the more you work with quadratic equations, the more confident and proficient you'll become in solving them.
Latest Posts
Latest Posts
-
Gcf Of 22 And 33
Sep 17, 2025
-
28 Celsius Is What Fahrenheit
Sep 17, 2025
-
28 Degrees Celcius To Farenheit
Sep 17, 2025
-
What Percentage Is 1 6
Sep 17, 2025
-
Gcf Of 24 And 12
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Solve 4x 2 25 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.