Gcf Of 24 And 12
keralas
Sep 17, 2025 · 7 min read
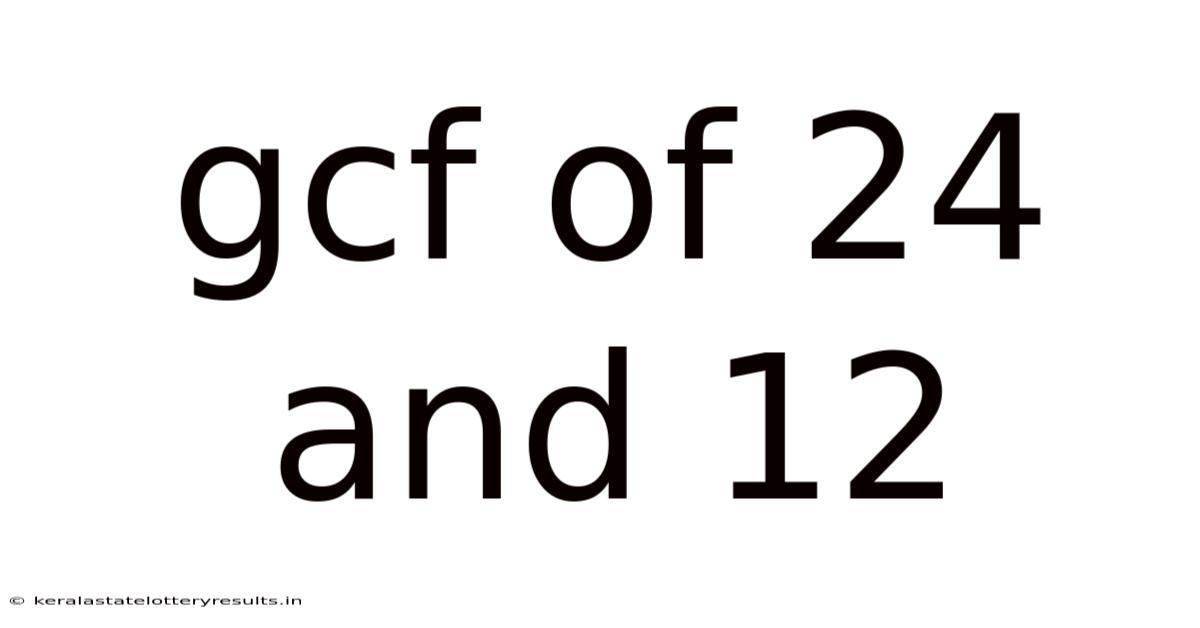
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 24 and 12: A Deep Dive
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. But understanding the underlying principles and exploring different methods for determining the GCF of numbers like 24 and 12 opens up a world of mathematical understanding, crucial for more advanced concepts in algebra, number theory, and even computer science. This article will not only show you how to find the GCF of 24 and 12 but also delve into the various methods, explaining the "why" behind the calculations and expanding your understanding of fundamental mathematical concepts.
Introduction: What is the Greatest Common Factor (GCF)?
The greatest common factor (GCF) of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. This article focuses specifically on finding the GCF of 24 and 12, but the methods we explore are applicable to any pair of integers.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 24 and 12. It involves listing all the factors of each number and then identifying the largest factor common to both.
Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
Factors of 12: 1, 2, 3, 4, 6, 12
By comparing the two lists, we can see that the common factors are 1, 2, 3, 4, 6, and 12. The largest of these common factors is 12. Therefore, the GCF of 24 and 12 is 12.
This method is easy to understand and visualize, making it ideal for beginners. However, it becomes less efficient as the numbers get larger, as listing all factors can be time-consuming and prone to errors.
Method 2: Prime Factorization
Prime factorization involves expressing a number as the product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...). This method is more efficient than listing all factors, especially when dealing with larger numbers.
Let's find the prime factorization of 24 and 12:
- Prime factorization of 24: 24 = 2 x 2 x 2 x 3 = 2³ x 3
- Prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
Once we have the prime factorization of both numbers, we identify the common prime factors and their lowest powers. Both 24 and 12 have 2 and 3 as prime factors. The lowest power of 2 is 2² (from the factorization of 12), and the lowest power of 3 is 3¹ (present in both factorizations).
Therefore, the GCF is the product of these common prime factors raised to their lowest powers: 2² x 3 = 4 x 3 = 12.
This method is more systematic and efficient than listing factors, particularly for larger numbers. It provides a deeper understanding of the number's structure and lays the groundwork for more advanced mathematical concepts.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the GCF of two integers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean Algorithm to 24 and 12:
- Start with the larger number (24) and the smaller number (12).
- Subtract the smaller number from the larger number: 24 - 12 = 12
- Replace the larger number with the result (12), and keep the smaller number (12). We now have the numbers 12 and 12.
- Since both numbers are equal, the GCF is 12.
The Euclidean Algorithm efficiently avoids the need for prime factorization or extensive factor listing. Its iterative nature makes it suitable for computer implementation and is fundamental in many computational algorithms.
A more formal representation of the Euclidean Algorithm involves repeated division with remainders. We divide the larger number by the smaller number and find the remainder. Then, we replace the larger number with the smaller number and the smaller number with the remainder. We continue this process until the remainder is 0. The last non-zero remainder is the GCF.
Let's illustrate this with 24 and 12:
- Divide 24 by 12: 24 = 12 x 2 + 0
- The remainder is 0, which means the GCF is the last non-zero divisor, which is 12.
This method elegantly demonstrates the fundamental concept of divisibility and its relationship to the GCF.
The Significance of the GCF: Real-World Applications
Understanding the GCF is more than just an academic exercise. It has practical applications in various fields:
-
Simplifying Fractions: The GCF is essential for simplifying fractions to their lowest terms. For instance, the fraction 24/12 can be simplified to 2/1 (or simply 2) by dividing both the numerator and the denominator by their GCF, which is 12.
-
Problem Solving: Many real-world problems involve finding the GCF. For example, imagine you have 24 apples and 12 oranges, and you want to divide them into identical bags such that each bag contains the same number of apples and oranges. The GCF (12) determines the maximum number of bags you can make. Each bag would have 2 apples and 1 orange.
-
Geometry: The GCF is used in geometric problems involving finding the dimensions of squares or rectangles that can be tiled from a larger area.
-
Music: In music theory, the GCF helps determine the simplest ratio of frequencies for musical intervals.
Expanding the Concept: GCF of More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, we find the prime factorization of each number and then take the common prime factors raised to their lowest powers. For the Euclidean Algorithm, we can find the GCF of two numbers, and then find the GCF of the result and the third number, and so on.
For example, to find the GCF of 12, 24, and 36:
-
Prime Factorization:
- 12 = 2² x 3
- 24 = 2³ x 3
- 36 = 2² x 3² The common prime factors are 2 and 3. The lowest powers are 2² and 3¹. Therefore, the GCF is 2² x 3 = 12.
-
Euclidean Algorithm (iterative approach):
- Find the GCF of 12 and 24 (which is 12).
- Find the GCF of 12 and 36 (which is 12). Therefore, the GCF of 12, 24, and 36 is 12.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they have no common factors other than 1.
Q: Is there a limit to the size of numbers for which we can find the GCF?
A: Theoretically, no. The Euclidean Algorithm and prime factorization can be used to find the GCF of arbitrarily large numbers, although the computational time may increase for extremely large numbers.
Q: Can negative numbers have a GCF?
A: Yes, the GCF of negative numbers is found by considering the absolute values of the numbers. The GCF of -12 and -24 is the same as the GCF of 12 and 24, which is 12.
Conclusion: Mastering the GCF
Finding the greatest common factor of two numbers, like 24 and 12, is a fundamental concept in mathematics. While seemingly simple, understanding the different methods – listing factors, prime factorization, and the Euclidean Algorithm – provides a deeper appreciation for number theory and its applications. This understanding forms the foundation for more advanced mathematical concepts and problem-solving skills, impacting various fields from computer science to music theory. By mastering the GCF, you are not only strengthening your arithmetic skills but also building a solid base for future mathematical explorations. Remember, the key is to choose the method that best suits the numbers and your level of understanding. Practice is essential to build proficiency and confidence in applying these methods.
Latest Posts
Latest Posts
-
What Is 20 Of 190
Sep 17, 2025
-
Algebra Equations That Equal 16
Sep 17, 2025
-
Is 15 An Even Number
Sep 17, 2025
-
Whats 30 Percent Of 80
Sep 17, 2025
-
Isosceles Triangle Lines Of Symmetry
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 24 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.