Lcm Of 2 And 10
keralas
Sep 15, 2025 · 6 min read
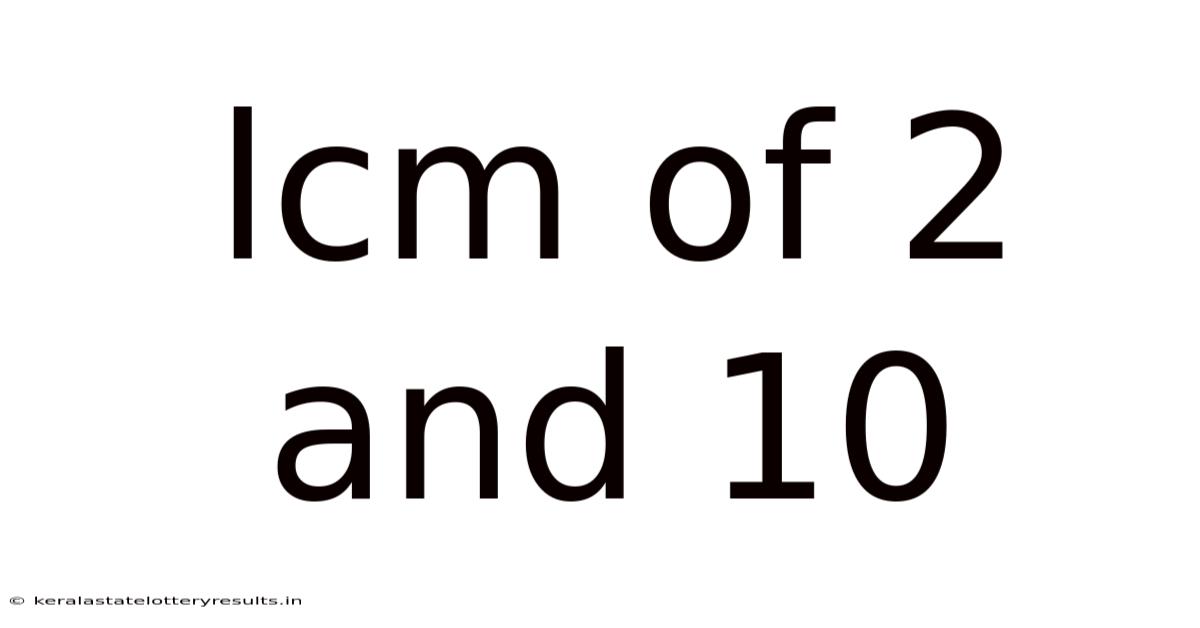
Table of Contents
Unveiling the LCM: A Deep Dive into the Least Common Multiple of 2 and 10
Finding the least common multiple (LCM) might seem like a simple arithmetic task, especially when dealing with small numbers like 2 and 10. However, understanding the underlying concepts and different methods for calculating the LCM provides a strong foundation for tackling more complex mathematical problems. This article will delve into the LCM of 2 and 10, exploring various approaches and explaining the significance of this fundamental concept in mathematics. We'll move beyond a simple answer and explore the 'why' behind the calculations, making the concept relatable and accessible to everyone, regardless of their mathematical background.
Understanding the Fundamentals: LCM Defined
Before we jump into calculating the LCM of 2 and 10, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. This concept is crucial in various areas of mathematics, including fractions, simplifying expressions, and solving problems related to cycles and periodic events.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 2 and 10. We simply list the multiples of each number until we find the smallest multiple that appears in both lists.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...
- Multiples of 10: 10, 20, 30, 40, 50, ...
By comparing the two lists, we can easily see that the smallest number present in both is 10. Therefore, the LCM of 2 and 10 is 10.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the concept. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
-
Prime Factorization of 2: 2 is itself a prime number, so its prime factorization is simply 2.
-
Prime Factorization of 10: 10 can be factored as 2 x 5.
-
Finding the LCM: To find the LCM using prime factorization, we identify the highest power of each prime factor present in the factorizations. In this case:
- The highest power of 2 is 2¹ = 2.
- The highest power of 5 is 5¹ = 5.
Multiplying these highest powers together gives us the LCM: 2 x 5 = 10.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) are closely related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers. This relationship provides another way to calculate the LCM.
-
Finding the GCD of 2 and 10: The greatest common divisor of 2 and 10 is 2, as 2 is the largest number that divides both 2 and 10 without leaving a remainder.
-
Applying the Formula: The formula relating LCM and GCD is:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
Substituting the values:
LCM(2, 10) x GCD(2, 10) = 2 x 10 LCM(2, 10) x 2 = 20 LCM(2, 10) = 20 / 2 = 10
Visual Representation: Understanding LCM through Diagrams
Visual aids can significantly enhance comprehension. Consider representing the multiples of 2 and 10 using number lines or Venn diagrams. A number line visually demonstrates the progression of multiples, making it easier to identify the smallest common multiple. A Venn diagram could illustrate the overlap of the sets of multiples, clearly highlighting the LCM as the smallest element in the intersection. These methods are particularly useful for teaching younger students or those who benefit from visual learning.
The Significance of LCM in Real-World Applications
The seemingly simple concept of the LCM has far-reaching applications in various fields:
-
Scheduling: Imagine two buses arriving at a station at different intervals. The LCM helps determine when both buses will arrive at the station simultaneously. For example, if one bus arrives every 2 hours and another every 10 hours, they will both arrive together after 10 hours (the LCM of 2 and 10).
-
Fractions: When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to create a common denominator, simplifying the calculation.
-
Cyclic Processes: In fields like engineering and physics, many processes are cyclical or periodic. The LCM helps determine when different cycles will coincide or align, crucial for coordinating events or predicting occurrences.
-
Pattern Recognition: Recognizing patterns and cycles often involves identifying the LCM. Understanding these repetitions is vital in areas like cryptography, signal processing, and even music theory.
Extending the Concept: LCM of More Than Two Numbers
The methods discussed above can be extended to find the LCM of more than two numbers. For prime factorization, we consider all prime factors from all numbers, taking the highest power of each. For the listing method, we list multiples of all numbers until we find the smallest common multiple. For the GCD method, we can use iterative approaches to find the LCM for multiple numbers.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between LCM and GCD?
- A: The LCM is the smallest common multiple, while the GCD is the greatest common divisor. They are inversely related; a larger GCD means a smaller LCM, and vice versa.
-
Q: Can the LCM of two numbers be one of the numbers?
- A: Yes, if one number is a multiple of the other, the LCM will be the larger number. In our example, 10 is a multiple of 2, and the LCM is 10.
-
Q: What if the numbers have no common factors other than 1?
- A: If the numbers are relatively prime (meaning their GCD is 1), their LCM will be the product of the two numbers.
-
Q: Are there any shortcuts or tricks for finding the LCM?
- A: For small numbers, listing multiples is quickest. For larger numbers, prime factorization is generally more efficient. The GCD method provides an alternative approach. Understanding the relationships between these methods allows you to choose the most appropriate strategy for a given problem.
Conclusion: Mastering the LCM – A Building Block of Mathematics
Understanding the LCM is not just about memorizing formulas or applying algorithms. It's about grasping the fundamental principles of divisibility, prime factorization, and the relationships between different mathematical concepts. By mastering the LCM, you're developing essential skills that are applicable across various mathematical disciplines and practical scenarios. The methods presented here provide a comprehensive toolkit to tackle LCM problems with confidence, from simple arithmetic to more complex mathematical challenges. Whether you're a student, a teacher, or simply someone curious about the beauty of mathematics, understanding the LCM of 2 and 10 – and the broader concept itself – opens doors to a deeper appreciation of the interconnectedness and elegance of numbers.
Latest Posts
Latest Posts
-
Whats 1 3 As A Fraction
Sep 15, 2025
-
Integral Of Cos Square X
Sep 15, 2025
-
0 3 Converted To A Fraction
Sep 15, 2025
-
Sin 3 Pi 4
Sep 15, 2025
-
Is 731 A Prime Number
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 And 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.