Sin 3 Pi / 4
keralas
Sep 15, 2025 · 5 min read
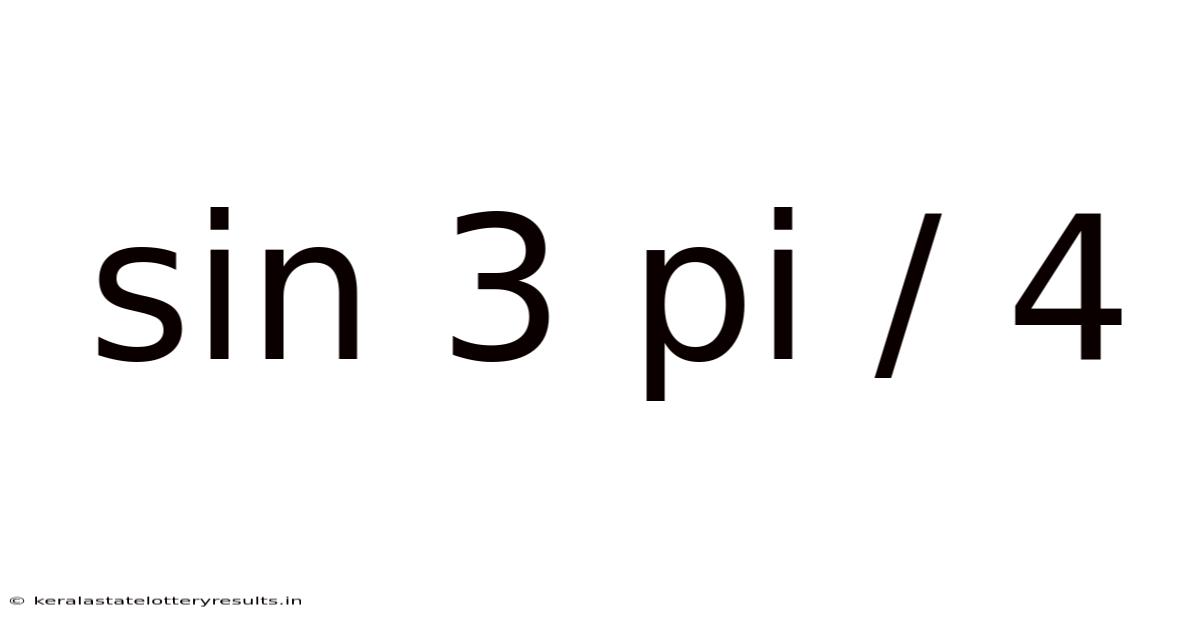
Table of Contents
Decoding sin(3π/4): A Deep Dive into Trigonometry
Understanding trigonometric functions like sine, cosine, and tangent is crucial in various fields, from physics and engineering to computer graphics and music theory. This article provides a comprehensive exploration of sin(3π/4), going beyond a simple numerical answer to delve into the underlying concepts and methods for calculating this value. We'll cover the unit circle, reference angles, and the properties of the sine function, ensuring a solid grasp of the topic for learners of all levels.
Introduction: Understanding the Sine Function
The sine function, denoted as sin(θ), is a fundamental trigonometric function that represents the ratio of the length of the side opposite an angle (θ) to the length of the hypotenuse in a right-angled triangle. However, its application extends far beyond right-angled triangles. In a unit circle (a circle with a radius of 1), the sine of an angle is the y-coordinate of the point where the terminal side of the angle intersects the circle. This geometric interpretation allows us to understand the sine function for any angle, not just those between 0 and π/2 (0 and 90 degrees).
The Unit Circle and Angles in Radians
The unit circle is a powerful tool for visualizing trigonometric functions. It's a circle with a radius of 1 centered at the origin (0,0) of a coordinate plane. Angles are measured in radians, where 2π radians corresponds to a full circle (360 degrees). Therefore, π radians is equivalent to 180 degrees, π/2 radians is 90 degrees, and so on. The angle 3π/4 radians is equivalent to (3/4) * 180° = 135°.
Finding sin(3π/4) using the Unit Circle
To find sin(3π/4), we locate the point on the unit circle that corresponds to an angle of 3π/4 radians (135°). This angle lies in the second quadrant. In the second quadrant, the x-coordinate is negative, and the y-coordinate is positive. The y-coordinate of this point represents sin(3π/4).
Remember that the coordinates of any point on the unit circle can be expressed as (cos θ, sin θ), where θ is the angle measured counterclockwise from the positive x-axis.
By using the symmetry of the unit circle, we can relate sin(3π/4) to a known sine value. The angle 3π/4 is π/4 radians (45°) away from π (180°). The reference angle is π/4, and since sine is positive in the second quadrant, we have:
sin(3π/4) = sin(π - π/4) = sin(π/4) = √2/2 ≈ 0.707
Understanding Reference Angles
A reference angle is the acute angle formed between the terminal side of an angle and the x-axis. It's always a positive angle between 0 and π/2 (0 and 90 degrees). Using reference angles simplifies the calculation of trigonometric functions for angles outside the first quadrant (0 to π/2).
To find the reference angle for 3π/4:
- Identify the quadrant: 3π/4 lies in the second quadrant.
- Find the difference from the nearest x-axis: The nearest x-axis is at π (180°). The difference is π - (3π/4) = π/4.
- The reference angle is π/4.
Since sin is positive in the second quadrant, sin(3π/4) = sin(π/4) = √2/2.
Steps to Calculate sin(3π/4): A Step-by-Step Guide
-
Convert to degrees (optional): 3π/4 radians is equal to (3π/4) * (180°/π) = 135°. This step is helpful for visualization.
-
Identify the quadrant: 135° lies in the second quadrant.
-
Determine the reference angle: The reference angle is 180° - 135° = 45°.
-
Find the sine of the reference angle: sin(45°) = √2/2.
-
Consider the sign: Since sine is positive in the second quadrant, sin(135°) = √2/2.
Explanation using Trigonometric Identities
We can also use trigonometric identities to determine sin(3π/4). One useful identity is the sine subtraction formula:
sin(A - B) = sin A cos B - cos A sin B
Let A = π and B = π/4. Then:
sin(π - π/4) = sin(π)cos(π/4) - cos(π)sin(π/4)
Since sin(π) = 0 and cos(π) = -1, we have:
sin(π - π/4) = 0 * cos(π/4) - (-1) * sin(π/4) = sin(π/4) = √2/2
Frequently Asked Questions (FAQs)
-
Q: Why is sin(3π/4) positive?
- A: The sine function is positive in the first and second quadrants. Since 3π/4 lies in the second quadrant, its sine value is positive.
-
Q: Can I use a calculator to find sin(3π/4)?
- A: Yes, ensure your calculator is in radian mode. Inputting sin(3π/4) will directly give you the approximate decimal value.
-
Q: What are the applications of understanding sin(3π/4)?
- A: Understanding this concept is crucial in various areas like physics (oscillations, waves), engineering (signal processing), and computer graphics (modeling curves and animations).
-
Q: How does the sine function relate to the cosine function?
- A: Sine and cosine are cofunctions, meaning sin(θ) = cos(π/2 - θ) and cos(θ) = sin(π/2 - θ). This relationship is evident in the unit circle.
-
Q: What is the difference between degrees and radians?
- A: Degrees and radians are two different units for measuring angles. Degrees divide a circle into 360 parts, while radians relate the angle to the radius of a circle. 2π radians equal 360 degrees. Radians are generally preferred in calculus and higher-level mathematics.
Conclusion: Mastering Trigonometric Functions
Understanding sin(3π/4) goes beyond simply knowing its numerical value (√2/2). It involves a deeper comprehension of the unit circle, reference angles, and the behavior of the sine function across different quadrants. Mastering these concepts is fundamental for success in trigonometry and its numerous applications in various scientific and technological fields. This detailed explanation provides a robust foundation for further exploration of trigonometric functions and their significance in mathematics and beyond. By utilizing the unit circle, reference angles, and trigonometric identities, you can confidently tackle similar problems and build a strong understanding of this crucial mathematical concept. Remember to practice regularly to solidify your understanding and develop your problem-solving skills in trigonometry.
Latest Posts
Latest Posts
-
Is 2011 A Prime Number
Sep 15, 2025
-
One Fourth Plus One Fourth
Sep 15, 2025
-
What Times What Equals 100
Sep 15, 2025
-
5 9 In Metric System
Sep 15, 2025
-
Is 329 A Prime Number
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Sin 3 Pi / 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.