Is 5/16th Bigger Than 1/4
keralas
Sep 12, 2025 · 5 min read
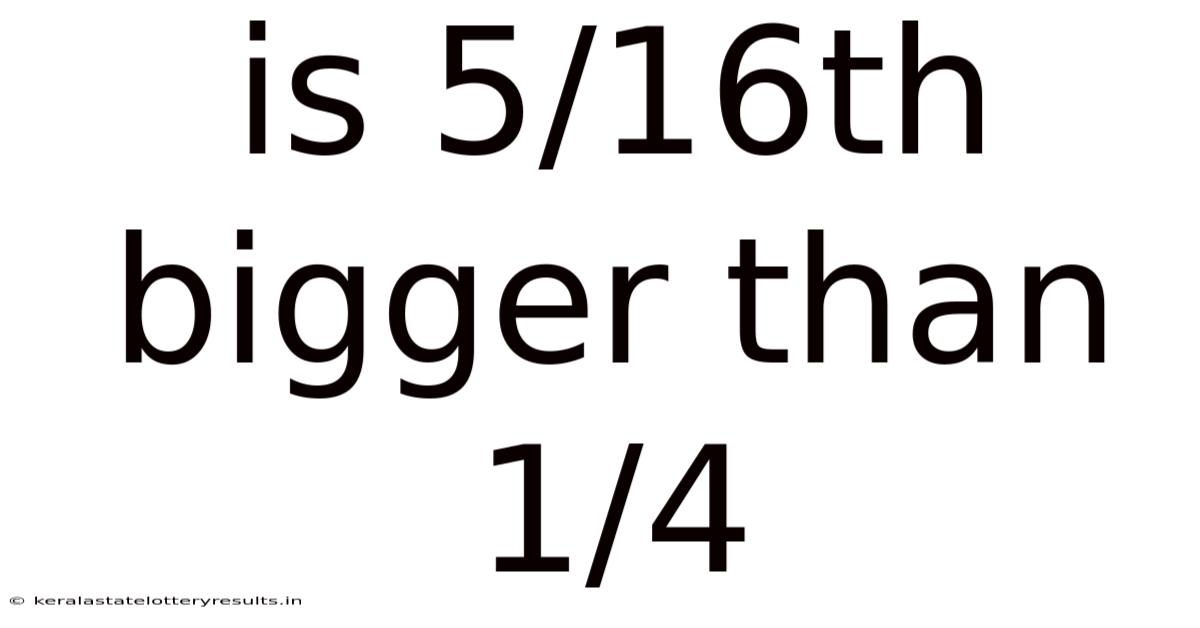
Table of Contents
Is 5/16th Bigger Than 1/4? A Deep Dive into Fraction Comparison
Are you struggling to compare fractions? Determining whether 5/16 is bigger than 1/4 might seem simple at first glance, but understanding the underlying principles is crucial for mastering fractions. This article will guide you through a step-by-step comparison of these two fractions, exploring various methods and providing a solid foundation for future fraction comparisons. We'll go beyond a simple answer, delving into the 'why' behind the comparison and equipping you with the tools to confidently tackle similar problems.
Introduction: Understanding Fractions
Before we dive into comparing 5/16 and 1/4, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For instance, in the fraction 1/4, the numerator (1) signifies one part, and the denominator (4) indicates that the whole is divided into four equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves converting both fractions so they share the same denominator. The easiest way to do this is to find the least common multiple (LCM) of the denominators.
Let's compare 5/16 and 1/4. The denominators are 16 and 4. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 16 are 16, 32, 48... The least common multiple of 4 and 16 is 16.
Now, we convert 1/4 to an equivalent fraction with a denominator of 16. To do this, we multiply both the numerator and the denominator by 4:
(1 * 4) / (4 * 4) = 4/16
Now we can easily compare 5/16 and 4/16. Since 5 > 4, we can conclude that 5/16 is bigger than 4/16, and therefore 5/16 is bigger than 1/4.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This is particularly useful when comparing fractions that don't easily share a common denominator. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 5/16 = 0.3125
- 1/4 = 0.25
By comparing the decimal values, we see that 0.3125 > 0.25, confirming that 5/16 is bigger than 1/4.
Method 3: Visual Representation
Visualizing fractions can be helpful, especially for beginners. Imagine a pizza cut into 16 slices. 5/16 represents 5 slices out of the 16. Now imagine another pizza cut into 4 slices. 1/4 represents 1 slice out of the 4. While it might seem difficult to directly compare the two pizzas, if we divide the second pizza into 16 slices (by cutting each slice into four smaller ones), we would have 4 slices representing 1/4. Clearly, 5 slices (5/16) are more than 4 slices (4/16). This visual representation reinforces the conclusion that 5/16 is bigger than 1/4.
Method 4: Cross-Multiplication
Cross-multiplication is a quick method for comparing two fractions. We multiply the numerator of the first fraction by the denominator of the second fraction and vice-versa. The fraction with the larger product is the larger fraction.
Let's apply this to 5/16 and 1/4:
- 5 * 4 = 20
- 16 * 1 = 16
Since 20 > 16, we confirm that 5/16 is bigger than 1/4.
Further Exploration: Understanding Fraction Magnitude
Understanding fraction magnitude involves grasping the relationship between the numerator and the denominator. A larger numerator relative to the denominator indicates a larger fraction. Conversely, a smaller numerator relative to the denominator represents a smaller fraction.
Consider these examples:
- 1/2 (one-half) is greater than 1/4 (one-quarter).
- 3/4 (three-quarters) is greater than 1/2 (one-half).
- 7/8 (seven-eighths) is greater than 3/4 (three-quarters).
In our case, 5/16 is closer to 1/3 than to 1/2. 1/4 is exactly halfway between 0 and 1/2. The proximity of the fraction to 1/2 also helps to get a qualitative sense of the size of the fraction. The closer to 1/2, the larger the fraction is.
Practical Applications of Fraction Comparison
Comparing fractions is a fundamental skill with widespread practical applications:
- Cooking and Baking: Following recipes often requires adjusting ingredient quantities, which necessitates comparing fractions.
- Construction and Engineering: Accurate measurements in construction and engineering projects rely heavily on precise fraction comparisons.
- Finance and Accounting: Calculating percentages, interest rates, and proportions often involves working with fractions.
- Data Analysis: Interpreting data presented in fractional form necessitates understanding fraction magnitude.
Frequently Asked Questions (FAQs)
-
Q: What if the fractions have different denominators and finding a common denominator is difficult?
A: In such cases, converting to decimals or using cross-multiplication is often the most efficient approach.
-
Q: Are there other methods to compare fractions besides the ones discussed?
A: Yes, some advanced methods exist for comparing fractions, including using their decimal approximations or comparing their positions on a number line.
-
Q: How can I improve my skills in comparing fractions?
A: Practice is key! Solve various fraction comparison problems, using different methods to build proficiency and understanding.
-
Q: Can I use a calculator to compare fractions?
A: While you can convert fractions to decimals using a calculator, understanding the underlying mathematical principles is crucial for developing a strong grasp of the concept.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a crucial skill in mathematics and has numerous practical applications in everyday life. Whether you use the common denominator method, decimal conversion, visual representation, or cross-multiplication, the key is to understand the underlying concepts. Through practice and consistent application of these methods, you will confidently tackle fraction comparisons of any complexity. Remember, understanding the relationship between the numerator and denominator is fundamental to accurately assessing the magnitude of a fraction. By mastering these techniques, you'll not only answer "Is 5/16 bigger than 1/4?" but you'll also gain the ability to compare any pair of fractions with ease and confidence. Keep practicing and soon you will master the art of fraction comparison!
Latest Posts
Latest Posts
-
Fastest Mile Per Hour Human
Sep 12, 2025
-
How Do You Times Percentages
Sep 12, 2025
-
Which Choices Are Real Numbers
Sep 12, 2025
-
Whats 5 8 As A Percent
Sep 12, 2025
-
4 1 8 To Decimal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 5/16th Bigger Than 1/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.