Is 1/2 Bigger Than 3/8
keralas
Sep 12, 2025 · 6 min read
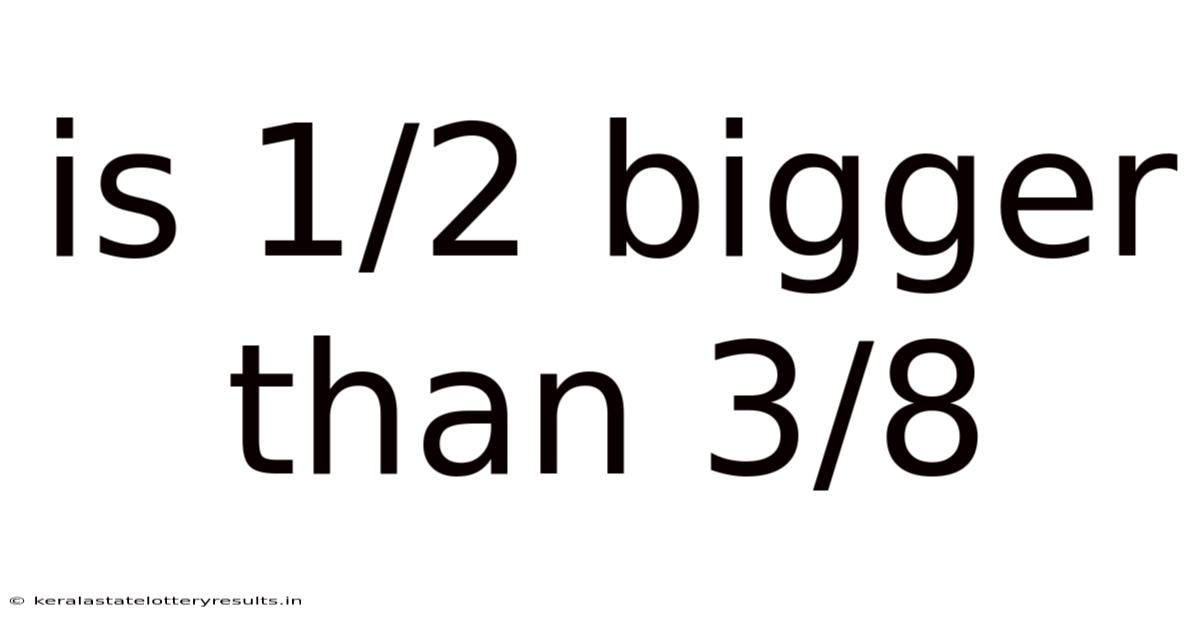
Table of Contents
Is 1/2 Bigger Than 3/8? A Deep Dive into Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article will thoroughly explore the question: "Is 1/2 bigger than 3/8?" We'll delve into various methods for comparing fractions, providing a solid understanding of the concepts involved, and leaving you confident in tackling similar comparisons in the future. This will cover different approaches, including visual representations, equivalent fractions, and decimal conversions, solidifying your understanding of fractional relationships.
Introduction: Understanding Fractions
Before comparing 1/2 and 3/8, let's establish a foundational understanding of fractions. A fraction represents a part of a whole. It's composed of two key parts:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2, the numerator (1) signifies that we have one part, and the denominator (2) signifies that the whole is divided into two equal parts. Therefore, 1/2 represents one-half of a whole. Similarly, 3/8 means we have three parts out of a total of eight equal parts.
Method 1: Visual Representation
A simple and intuitive way to compare fractions is through visual representation. Imagine two identical circles.
- Circle 1: Divide this circle into two equal halves. Shade one half. This visually represents 1/2.
- Circle 2: Divide this circle into eight equal parts. Shade three of these parts. This visually represents 3/8.
By directly comparing the shaded areas, it becomes immediately apparent that the shaded area in Circle 1 (1/2) is larger than the shaded area in Circle 2 (3/8). This visual comparison provides a clear and immediate answer to our question: Yes, 1/2 is bigger than 3/8.
Method 2: Finding a Common Denominator
A more algebraic approach involves finding a common denominator for both fractions. This means finding a number that is a multiple of both denominators (2 and 8). In this case, the least common multiple (LCM) of 2 and 8 is 8.
- Convert 1/2: To convert 1/2 to an equivalent fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
Now we can easily compare:
- 4/8 vs. 3/8
Since both fractions now have the same denominator, we can directly compare their numerators. 4 is greater than 3, therefore: 4/8 (which is equivalent to 1/2) is bigger than 3/8.
Method 3: Decimal Conversion
Another effective method is to convert both fractions into decimals. This is particularly helpful for making quick comparisons or when working with calculators.
- Convert 1/2 to a decimal: 1 ÷ 2 = 0.5
- Convert 3/8 to a decimal: 3 ÷ 8 = 0.375
Comparing the decimal values, 0.5 is clearly greater than 0.375. Therefore, 1/2 (0.5) is bigger than 3/8 (0.375).
Method 4: Cross-Multiplication
Cross-multiplication is a powerful technique for comparing two fractions. To use this method, we multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. Then we compare the results.
- Cross-multiply 1/2 and 3/8:
- (1 x 8) = 8
- (2 x 3) = 6
Since 8 > 6, 1/2 is bigger than 3/8.
This method directly compares the relative sizes of the fractions without the need for finding a common denominator or converting to decimals.
A Deeper Look at Fraction Comparison Techniques
The methods described above offer various approaches to comparing fractions. The choice of method often depends on personal preference and the complexity of the fractions involved. For simple fractions like 1/2 and 3/8, visual representation or direct comparison after finding a common denominator are often the most intuitive. However, for more complex fractions, decimal conversion or cross-multiplication might be more efficient.
Understanding these different methods empowers you to tackle a wider range of fraction comparison problems confidently. Each method provides a pathway to understanding the relative magnitudes of different fractional parts of a whole.
Practical Applications of Fraction Comparison
The ability to compare fractions is not just an academic exercise; it finds practical applications in many aspects of daily life:
- Cooking and Baking: Recipes often require precise measurements, and understanding fraction comparison is crucial for accurate ingredient proportions.
- Construction and Engineering: Precise measurements are critical in construction and engineering projects, and the ability to accurately compare fractions ensures the structural integrity and functionality of buildings and other structures.
- Finance: Understanding fractions is essential for managing finances, including calculating interest rates, discounts, and proportions of budgets.
- Data Analysis: In various fields, understanding fractions and their relative sizes is critical for interpreting data and drawing accurate conclusions.
Frequently Asked Questions (FAQ)
Q1: Are there any other ways to compare fractions?
A1: Yes, you could also use a number line to visualize the relative positions of the fractions. Plotting 1/2 and 3/8 on a number line clearly shows that 1/2 is to the right (and therefore larger) than 3/8.
Q2: What if the fractions have different denominators and are more complex?
A2: For more complex fractions, finding the least common denominator or using cross-multiplication is generally the most efficient approach. Decimal conversion is also a viable option, especially when using a calculator.
Q3: How can I improve my skills in comparing fractions?
A3: Practice is key! Work through numerous examples, trying different comparison methods. The more you practice, the more intuitive the process will become. Start with simple fractions and gradually progress to more complex ones. Use visual aids like diagrams and number lines to reinforce your understanding.
Q4: Is there a specific order of operations when comparing fractions using different methods?
A4: There isn't a strict order, but it's generally recommended to simplify fractions before comparing them. If you choose the common denominator method, finding the least common multiple is usually more efficient. For cross-multiplication, the order of multiplication doesn't affect the outcome but consistency is important for clarity.
Conclusion: Mastering Fraction Comparison
In conclusion, 1/2 is indeed bigger than 3/8. This article has explored various methods for comparing fractions – visual representation, finding a common denominator, decimal conversion, and cross-multiplication – each offering a unique approach to understanding the relative sizes of fractions. Mastering these techniques is crucial for a strong foundation in mathematics and for solving problems across numerous disciplines. Remember, consistent practice and employing the most suitable method for each problem are key to developing confidence and proficiency in fraction comparison. By understanding the underlying principles and practicing regularly, you'll build a strong foundation for tackling more complex mathematical concepts in the future.
Latest Posts
Latest Posts
-
Fastest Mile Per Hour Human
Sep 12, 2025
-
How Do You Times Percentages
Sep 12, 2025
-
Which Choices Are Real Numbers
Sep 12, 2025
-
Whats 5 8 As A Percent
Sep 12, 2025
-
4 1 8 To Decimal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 1/2 Bigger Than 3/8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.