Hcf Of 24 And 32
keralas
Sep 16, 2025 · 6 min read
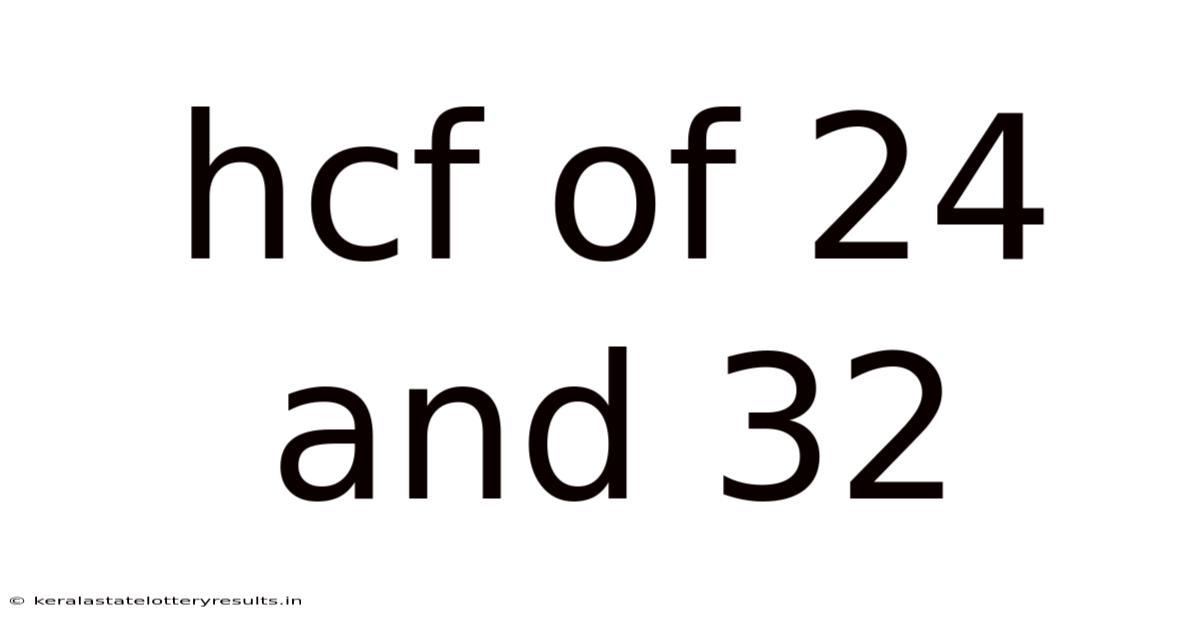
Table of Contents
Unveiling the Secrets of HCF: A Deep Dive into Finding the Highest Common Factor of 24 and 32
Finding the Highest Common Factor (HCF), also known as the Greatest Common Divisor (GCD), of two numbers might seem like a simple arithmetic task. But understanding the underlying principles and exploring different methods opens a window into fundamental number theory concepts. This article will provide a comprehensive exploration of how to find the HCF of 24 and 32, going beyond a simple answer to delve into the "why" and "how" behind the calculations. We'll explore multiple methods, discuss their applications, and even touch upon the real-world relevance of this seemingly basic mathematical concept.
Understanding the Concept of Highest Common Factor (HCF)
Before diving into the specific calculation for 24 and 32, let's establish a solid foundation. The HCF of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that is a factor of both numbers. Think of it like finding the largest shared building block of two different structures.
For instance, consider the factors of 12: 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The highest among these common factors is 6; therefore, the HCF of 12 and 18 is 6.
Understanding factors and divisors is crucial. A factor of a number is a whole number that divides the number exactly, leaving no remainder. A divisor is essentially the same thing – a number that divides another number completely. We often use these terms interchangeably.
Method 1: Prime Factorization Method
This method is a powerful and widely used technique for finding the HCF of any two numbers. It involves breaking down each number into its prime factors – the smallest prime numbers that multiply together to make the original number.
Steps:
-
Find the prime factorization of each number.
- 24: We can break 24 down as follows: 24 = 2 x 12 = 2 x 2 x 6 = 2 x 2 x 2 x 3 = 2³ x 3
- 32: Similarly, 32 can be factorized as: 32 = 2 x 16 = 2 x 2 x 8 = 2 x 2 x 2 x 4 = 2 x 2 x 2 x 2 x 2 = 2⁵
-
Identify the common prime factors. In this case, the only common prime factor is 2.
-
Find the lowest power of the common prime factors. The lowest power of 2 present in both factorizations is 2³.
-
Multiply the lowest powers of the common prime factors. In this instance, we only have one common prime factor (2), and its lowest power is 2³. Therefore, 2³ = 8.
Therefore, the HCF of 24 and 32 is 8.
Method 2: Listing Factors Method
This method is suitable for smaller numbers where listing all factors is relatively easy.
Steps:
-
List all factors of each number.
- Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
- Factors of 32: 1, 2, 4, 8, 16, 32
-
Identify the common factors. The common factors of 24 and 32 are 1, 2, 4, and 8.
-
Select the highest common factor. The largest number among the common factors is 8.
Therefore, the HCF of 24 and 32 is 8. This method, while straightforward for smaller numbers, becomes cumbersome and impractical for larger numbers.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the HCF of two numbers, particularly useful for larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
-
Divide the larger number by the smaller number and find the remainder.
32 ÷ 24 = 1 with a remainder of 8
-
Replace the larger number with the smaller number and the smaller number with the remainder. Now we find the HCF of 24 and 8.
-
Repeat the division process.
24 ÷ 8 = 3 with a remainder of 0
-
The HCF is the last non-zero remainder. Since the remainder is 0, the HCF is the last non-zero remainder, which was 8.
Therefore, the HCF of 24 and 32 is 8. The Euclidean algorithm is significantly more efficient than listing factors for larger numbers.
Why is finding the HCF important?
The seemingly simple task of finding the HCF has significant applications across various fields:
-
Simplifying Fractions: Finding the HCF helps in simplifying fractions to their lowest terms. For example, the fraction 24/32 can be simplified to 3/4 by dividing both the numerator and denominator by their HCF, which is 8.
-
Solving Word Problems: Many word problems in mathematics and real-world scenarios involve finding the HCF to determine the largest possible size or quantity. Imagine dividing a piece of land into equally sized squares – the HCF helps determine the largest possible square size.
-
Number Theory: The HCF forms the basis of many important concepts in number theory, including the least common multiple (LCM), which is closely related and often used in conjunction with the HCF.
-
Computer Science: The Euclidean algorithm, a highly efficient method for calculating the HCF, is fundamental in cryptography and other computational processes.
Frequently Asked Questions (FAQ)
Q: What is the difference between HCF and LCM?
A: The HCF (Highest Common Factor) is the largest number that divides two or more numbers without leaving a remainder. The LCM (Least Common Multiple) is the smallest number that is a multiple of two or more numbers. They are related; the product of the HCF and LCM of two numbers is equal to the product of the two numbers.
Q: Can the HCF of two numbers be 1?
A: Yes, if two numbers have no common factors other than 1, their HCF is 1. Such numbers are called relatively prime or coprime.
Q: Is there a limit to the number of methods for finding the HCF?
A: While the methods discussed here are the most common and widely used, there are other algorithms and approaches for finding the HCF. The choice of method often depends on the size of the numbers and the computational resources available.
Q: How can I verify if my calculated HCF is correct?
A: You can verify your HCF by ensuring that it divides both numbers without leaving a remainder. You can also check if it's the largest number that does so by comparing it to other common factors.
Conclusion
Finding the Highest Common Factor of 24 and 32, which is 8, is more than just a simple arithmetic exercise. It provides a gateway to understanding fundamental concepts in number theory and their practical applications. Through the prime factorization method, the listing factors method, and the efficient Euclidean algorithm, we've explored different approaches to solving this problem, each with its own strengths and limitations. Understanding these methods empowers you not only to solve similar problems but also to appreciate the underlying mathematical principles that govern them. This knowledge extends beyond the classroom, finding utility in various aspects of mathematics, computer science, and problem-solving in everyday life. Remember that the key to mastering these concepts lies in practice and understanding the underlying principles. So, grab your pencils, practice with different numbers, and soon you'll be a HCF expert!
Latest Posts
Latest Posts
-
90 Degrees Celsius To Fahrenheit
Sep 16, 2025
-
Gcf Of 42 And 24
Sep 16, 2025
-
Rearrange Expression Into Quadratic Form
Sep 16, 2025
-
Gcf Of 30 And 16
Sep 16, 2025
-
What Is 100 Of 15
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 24 And 32 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.