Gcf Of 18 And 6
keralas
Sep 14, 2025 · 7 min read
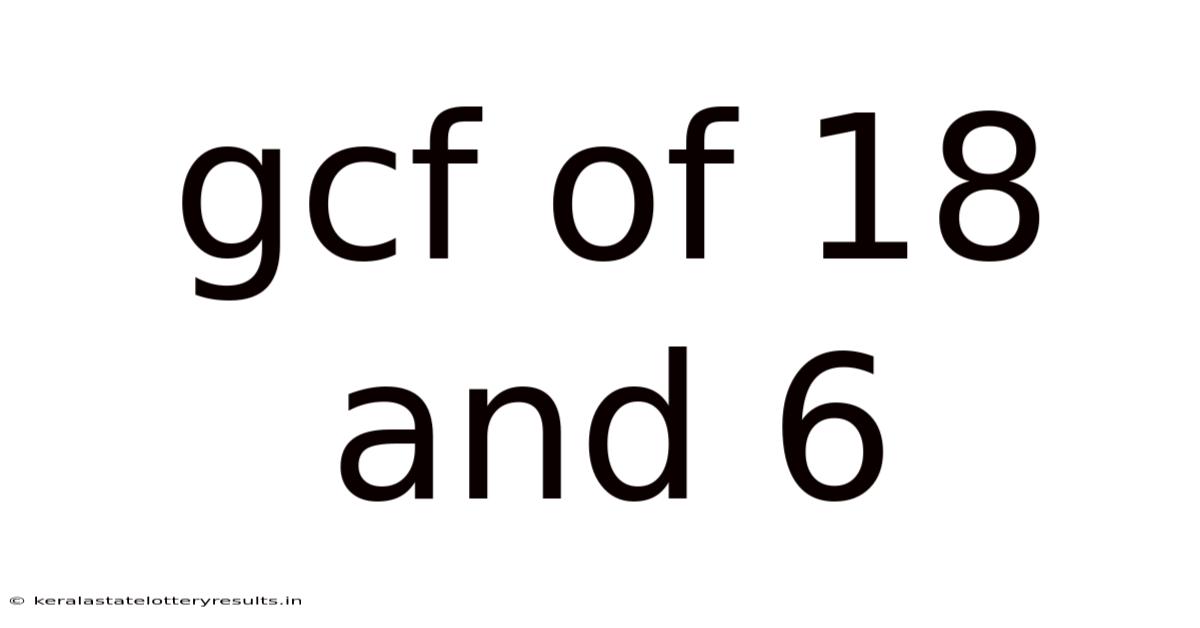
Table of Contents
Understanding the Greatest Common Factor (GCF) of 18 and 6: A Deep Dive
Finding the greatest common factor (GCF) of two numbers, like 18 and 6, might seem like a simple arithmetic task. However, understanding the underlying concepts and various methods for calculating the GCF provides a strong foundation for more advanced mathematical concepts. This article will delve into the GCF of 18 and 6, exploring different approaches, explaining the underlying principles, and demonstrating its practical applications. We'll move beyond a simple answer and explore the "why" behind the calculations, making this a valuable resource for students and anyone interested in strengthening their number sense.
What is the Greatest Common Factor (GCF)?
The Greatest Common Factor (GCF), also known as the greatest common divisor (GCD), is the largest number that divides evenly into two or more numbers without leaving a remainder. Think of it as the biggest number that's a factor of both numbers. For example, the factors of 6 are 1, 2, 3, and 6, while the factors of 18 are 1, 2, 3, 6, 9, and 18. The GCF of 6 and 18 is the largest number that appears in both lists – that's 6.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers. Let's find the GCF of 18 and 6 using this approach:
- List the factors of 18: 1, 2, 3, 6, 9, 18
- List the factors of 6: 1, 2, 3, 6
- Identify common factors: The numbers that appear in both lists are 1, 2, 3, and 6.
- Determine the greatest common factor: The largest number among the common factors is 6.
Therefore, the GCF of 18 and 6 is 6. This method works well for smaller numbers, but it can become cumbersome and time-consuming with larger numbers.
Method 2: Prime Factorization
Prime factorization is a more efficient method, especially for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Find the prime factorization of 18: 18 = 2 x 3 x 3 = 2 x 3²
- Find the prime factorization of 6: 6 = 2 x 3
- Identify common prime factors: Both 18 and 6 share a prime factor of 2 and a prime factor of 3.
- Multiply the common prime factors: The GCF is the product of the common prime factors. In this case, it's 2 x 3 = 6.
Therefore, the GCF of 18 and 6 is 6. This method is more efficient for larger numbers because it systematically breaks down the numbers into their fundamental components.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a powerful and efficient method for finding the GCF of two numbers, regardless of their size. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. Let's illustrate this with 18 and 6:
- Divide the larger number (18) by the smaller number (6): 18 ÷ 6 = 3 with a remainder of 0.
- Interpret the result: Since the remainder is 0, the smaller number (6) is the GCF.
Therefore, the GCF of 18 and 6 is 6. If there was a non-zero remainder, you would repeat the process, using the remainder and the previous divisor. This algorithm is particularly useful for finding the GCF of very large numbers, as it avoids the need to find all factors.
Understanding the Significance of the GCF
The GCF has several practical applications across various mathematical concepts and real-world scenarios:
-
Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 18/6 can be simplified by dividing both the numerator and denominator by their GCF (6), resulting in the simplified fraction 3/1 or simply 3.
-
Solving Word Problems: Many word problems involving equal sharing or grouping require finding the GCF to determine the largest possible size of groups or shares. For instance, if you have 18 apples and 6 oranges, and you want to divide them into equal groups with the same number of apples and oranges in each group, the GCF (6) will tell you the maximum number of groups you can make. Each group would have 3 apples and 1 orange.
-
Algebraic Simplification: In algebra, the GCF is used to simplify expressions by factoring out common factors. For example, the expression 18x + 6y can be simplified to 6(3x + y) by factoring out the GCF of 18 and 6, which is 6.
-
Geometric Applications: The GCF is used in geometry to find the dimensions of the largest possible square that can be used to tile a rectangle. For example, a rectangle with dimensions 18 units by 6 units can be tiled with squares of side length 6 units.
Least Common Multiple (LCM) and its Relationship with GCF
While we've focused on the GCF, it's important to understand its relationship with the Least Common Multiple (LCM). The LCM is the smallest number that is a multiple of both numbers. For 18 and 6:
- Multiples of 18: 18, 36, 54, 72...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
The smallest number that appears in both lists is 18. Therefore, the LCM of 18 and 6 is 18. There's a useful relationship between the GCF and LCM of two numbers (a and b):
LCM(a, b) * GCF(a, b) = a * b
In our case: LCM(18, 6) * GCF(18, 6) = 18 * 6 = 108. This relationship provides a quick way to find the LCM if you already know the GCF (or vice versa).
Extending the Concept: GCF of More Than Two Numbers
The methods we've discussed can be extended to find the GCF of more than two numbers. For example, to find the GCF of 18, 6, and 12:
-
Prime Factorization Method:
- 18 = 2 x 3²
- 6 = 2 x 3
- 12 = 2² x 3
The common prime factors are 2 and 3. The lowest power of 2 that appears in all factorizations is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCF(18, 6, 12) = 2 x 3 = 6.
-
Euclidean Algorithm (Extended): The Euclidean algorithm can be extended to more than two numbers by repeatedly finding the GCF of pairs of numbers. For example:
- Find GCF(18, 6) = 6
- Then find GCF(6, 12) = 6
Therefore, the GCF(18, 6, 12) = 6.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they don't share any common factors other than 1.
Q: Can the GCF of two numbers be larger than the smaller number?
A: No, the GCF can never be larger than the smaller of the two numbers.
Q: Is there a quick way to find the GCF of very large numbers?
A: The Euclidean algorithm is the most efficient method for finding the GCF of very large numbers. Computer programs often use this algorithm because of its speed and efficiency.
Q: What's the difference between GCF and LCM?
A: The GCF is the largest number that divides both numbers evenly, while the LCM is the smallest number that is a multiple of both numbers. They are related through the equation: LCM(a, b) * GCF(a, b) = a * b.
Conclusion
Finding the greatest common factor is a fundamental concept in mathematics with numerous applications. While the listing factors method is suitable for small numbers, prime factorization and the Euclidean algorithm are more efficient for larger numbers. Understanding these methods not only helps in solving arithmetic problems but also provides a solid foundation for more advanced mathematical concepts. Remember to practice different methods to build your understanding and choose the most appropriate technique depending on the context and the size of the numbers involved. Mastering the GCF concept will significantly enhance your mathematical abilities and problem-solving skills.
Latest Posts
Latest Posts
-
Cube Root Of 81 Simplified
Sep 14, 2025
-
Converse Of The Statement Example
Sep 14, 2025
-
What Is Xxv In Numbers
Sep 14, 2025
-
15 Percent Into A Fraction
Sep 14, 2025
-
7 Times What Equals 42
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 18 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.