What Is Sin 45 Degree
keralas
Sep 14, 2025 · 6 min read
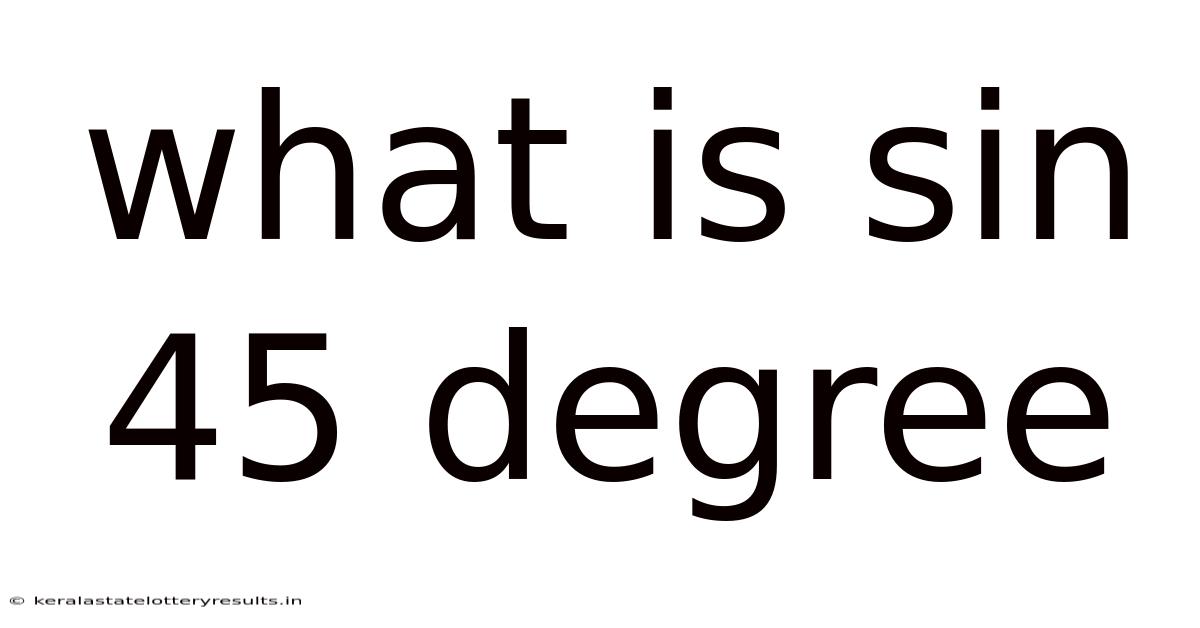
Table of Contents
Understanding Sin 45 Degrees: A Deep Dive into Trigonometry
What is sin 45 degrees? This seemingly simple question opens the door to a fascinating exploration of trigonometry, a branch of mathematics crucial for understanding angles, triangles, and their relationships. This article will not only answer the question directly but will also delve into the underlying principles, providing a comprehensive understanding of the concept for students and enthusiasts alike. We will cover the definition of sine, explore its calculation for a 45-degree angle, examine its application in various fields, and address common questions and misconceptions.
Introduction to Trigonometric Functions
Trigonometry, at its core, deals with the relationships between angles and sides of triangles. Three primary functions form the foundation: sine (sin), cosine (cos), and tangent (tan). These functions are defined using a right-angled triangle (a triangle with one 90-degree angle).
Consider a right-angled triangle with:
- Hypotenuse: The longest side, opposite the right angle.
- Opposite side: The side opposite the angle we're interested in.
- Adjacent side: The side next to the angle we're interested in (not the hypotenuse).
The sine of an angle (θ) is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse:
sin θ = Opposite / Hypotenuse
Calculating Sin 45 Degrees
To find sin 45 degrees, we need a right-angled triangle containing a 45-degree angle. The unique property of a 45-degree angle in a right-angled triangle is that it creates an isosceles right-angled triangle – meaning two of its sides (the opposite and adjacent) are equal in length.
Let's assume the lengths of the opposite and adjacent sides are both 'x'. Using the Pythagorean theorem (a² + b² = c²), where 'a' and 'b' are the lengths of the two shorter sides and 'c' is the length of the hypotenuse, we can find the length of the hypotenuse:
x² + x² = Hypotenuse² 2x² = Hypotenuse² Hypotenuse = x√2
Now, we can calculate sin 45 degrees:
sin 45° = Opposite / Hypotenuse = x / (x√2) = 1 / √2
To rationalize the denominator (remove the square root from the bottom), we multiply both the numerator and denominator by √2:
sin 45° = (1 * √2) / (√2 * √2) = √2 / 2
Therefore, sin 45° ≈ 0.7071
The Unit Circle and Sin 45 Degrees
Another way to visualize and understand sin 45 degrees is through the unit circle. The unit circle is a circle with a radius of 1 centered at the origin of a coordinate plane. Any point on the unit circle can be represented by its coordinates (cos θ, sin θ), where θ is the angle formed between the positive x-axis and the line connecting the origin to that point.
For a 45-degree angle, the point on the unit circle lies at (√2/2, √2/2). The y-coordinate of this point represents the sine of the angle, which is √2/2, confirming our previous calculation.
Applications of Sin 45 Degrees
The sine function, and specifically the value of sin 45 degrees, finds extensive application in various fields:
-
Physics: Calculating projectile motion, analyzing wave phenomena, and solving problems in mechanics often involve the sine function. Understanding sin 45 degrees is crucial for determining the vertical component of velocity in projectile motion at a 45-degree launch angle.
-
Engineering: Structural analysis, surveying, and the design of various mechanisms rely heavily on trigonometric calculations. Determining forces and angles in truss structures frequently necessitates the use of sine and cosine functions.
-
Computer Graphics: Generating realistic images and animations requires accurate calculations of angles and distances. The sine function plays a significant role in transformations, rotations, and perspective projections.
-
Navigation: Determining distances and bearings using triangulation techniques relies on trigonometric principles. Understanding angles and their sine values is essential for accurate navigation, especially in aerial and marine contexts.
-
Astronomy: Calculating celestial positions and distances involves extensive use of trigonometry. Understanding the sine function is fundamental to many astronomical calculations.
Beyond the Basics: Exploring Related Concepts
Understanding sin 45 degrees provides a solid foundation for exploring more complex trigonometric concepts:
-
Other Trigonometric Functions: The cosine of 45 degrees (cos 45°) is also √2/2, reflecting the symmetry of the isosceles right-angled triangle. The tangent of 45 degrees (tan 45°) equals 1 (Opposite/Adjacent = x/x = 1).
-
Inverse Trigonometric Functions: Inverse trigonometric functions, such as arcsin (sin⁻¹), allow you to find the angle given the sine value. For example, sin⁻¹(√2/2) = 45°.
-
Trigonometric Identities: Numerous trigonometric identities relate different trigonometric functions. These identities are valuable for simplifying complex expressions and solving trigonometric equations.
-
Radians: While degrees are a common unit for measuring angles, radians are another unit often used in higher-level mathematics and physics. 45 degrees is equivalent to π/4 radians.
Frequently Asked Questions (FAQ)
Q: Why is sin 45 degrees equal to √2/2?
A: This value stems from the properties of an isosceles right-angled triangle. The equal sides and the hypotenuse, calculated using the Pythagorean theorem, lead directly to this ratio.
Q: Is sin 45 degrees always √2/2?
A: Yes, the sine of a 45-degree angle is always √2/2, regardless of the size of the isosceles right-angled triangle. The ratio remains constant.
Q: How do I use sin 45 degrees in calculations?
A: You substitute √2/2 (or its approximate decimal value, 0.7071) into any equation involving sin 45°. For example, in projectile motion, you might use it to calculate the vertical component of velocity.
Q: Are there other angles with easily calculable sine values?
A: Yes, angles like 0°, 30°, 60°, and 90° also have easily calculable sine values (0, 1/2, √3/2, and 1, respectively). These values are often derived from equilateral triangles and their properties.
Q: What happens if I use the sine function with an angle greater than 90 degrees?
A: The sine function is defined for all angles, not just those in right-angled triangles. For angles greater than 90 degrees, the unit circle provides a visual representation, and the sine value reflects the y-coordinate of the corresponding point on the circle.
Conclusion
Understanding sin 45 degrees is not just about memorizing a numerical value; it's about grasping the fundamental principles of trigonometry and their broad applications. From the simple isosceles right-angled triangle to the complexities of advanced physics and engineering, the sine function and its value at 45 degrees form an essential building block in various scientific and technical disciplines. By exploring the concepts presented in this article, you’ve gained a deeper appreciation for this fundamental trigonometric concept and its crucial role in solving real-world problems. Further exploration into the wider field of trigonometry will undoubtedly reveal even more fascinating applications and interconnected concepts.
Latest Posts
Latest Posts
-
6 Yards How Many Inches
Sep 14, 2025
-
Is 88 A Perfect Square
Sep 14, 2025
-
Sin 40 Degrees Times 3
Sep 14, 2025
-
Is 311 A Prime Number
Sep 14, 2025
-
Negative 15 Celsius To Fahrenheit
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is Sin 45 Degree . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.