10 15 In Simplest Form
keralas
Sep 17, 2025 · 6 min read
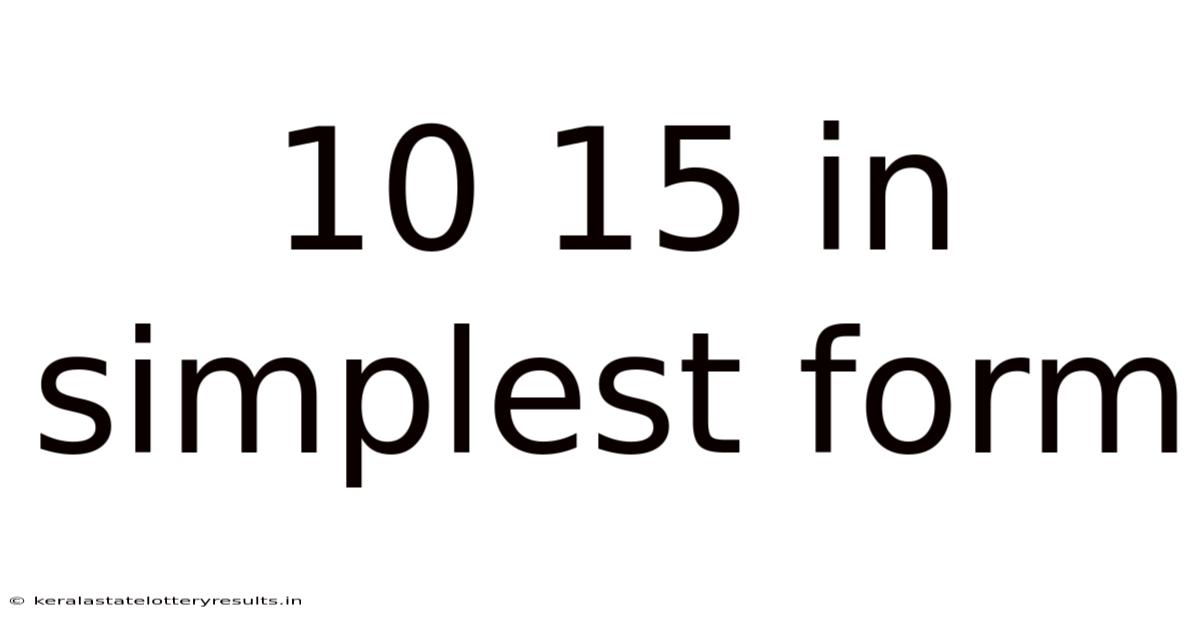
Table of Contents
Simplifying Fractions: A Deep Dive into 10/15
Understanding fractions is a fundamental building block in mathematics. This article will explore the simplification of fractions, using the example of 10/15, and provide a comprehensive understanding of the underlying principles. We’ll delve into the process step-by-step, explain the mathematical reasoning behind it, and address common questions and misconceptions. By the end, you’ll not only know the simplest form of 10/15 but also possess the skills to simplify any fraction with confidence.
Introduction: What Does Simplifying Fractions Mean?
Simplifying a fraction means reducing it to its lowest terms. This means finding an equivalent fraction where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In simpler terms, you're finding the smallest whole numbers that represent the same ratio. Think of it like reducing a recipe: you can halve the ingredients, or even use thirds, but the final dish will still taste the same. Similarly, simplifying a fraction doesn't change its value, just its representation.
Understanding Factors and Greatest Common Factors (GCF)
Before we tackle 10/15, let’s review some key concepts. A factor is a number that divides exactly into another number without leaving a remainder. For example, the factors of 10 are 1, 2, 5, and 10. The factors of 15 are 1, 3, 5, and 15.
The Greatest Common Factor (GCF), also known as the highest common factor (HCF), is the largest number that is a factor of two or more numbers. Finding the GCF is crucial for simplifying fractions. To find the GCF of 10 and 15, we can list their factors:
- Factors of 10: 1, 2, 5, 10
- Factors of 15: 1, 3, 5, 15
The largest number that appears in both lists is 5. Therefore, the GCF of 10 and 15 is 5.
Step-by-Step Simplification of 10/15
Now, let's simplify 10/15 using the GCF we just found:
-
Find the GCF: As determined above, the GCF of 10 and 15 is 5.
-
Divide the numerator and denominator by the GCF: We divide both the numerator (10) and the denominator (15) by the GCF (5):
10 ÷ 5 = 2 15 ÷ 5 = 3
-
Write the simplified fraction: The simplified fraction is 2/3.
Therefore, 10/15 simplified to its lowest terms is 2/3.
Visual Representation: Understanding Fractions
Let's visualize this simplification. Imagine you have a pizza cut into 15 equal slices. You have 10 of these slices (10/15). If you group these slices into sets of 5, you'll have 2 groups of 5 slices each. The entire pizza is now conceptually divided into 3 groups of 5 slices, and you possess 2 of these groups. This visually represents the simplified fraction 2/3.
Alternative Methods for Finding the GCF
While listing factors works well for smaller numbers, it can become cumbersome for larger numbers. Here are two alternative methods for finding the GCF:
-
Prime Factorization: This method involves breaking down each number into its prime factors (numbers only divisible by 1 and themselves). Let's apply this to 10 and 15:
- 10 = 2 x 5
- 15 = 3 x 5
The common prime factor is 5. Therefore, the GCF is 5.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCF. Let's apply this to 10 and 15:
- Divide the larger number (15) by the smaller number (10): 15 ÷ 10 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (5): 10 ÷ 5 = 2 with a remainder of 0.
- The last non-zero remainder is 5, so the GCF is 5.
Simplifying Fractions with Larger Numbers
The principles remain the same when dealing with larger numbers. Let's consider the fraction 48/72:
-
Find the GCF: Using prime factorization:
- 48 = 2 x 2 x 2 x 2 x 3
- 72 = 2 x 2 x 2 x 3 x 3
The common prime factors are 2 x 2 x 2 x 3 = 24. Therefore, the GCF is 24.
-
Divide by the GCF:
48 ÷ 24 = 2 72 ÷ 24 = 3
-
Simplified Fraction: The simplified fraction is 2/3.
This demonstrates that even with larger numbers, the process remains consistent. The key is efficiently finding the GCF.
Common Mistakes to Avoid
-
Incorrectly identifying the GCF: Carefully examine the factors of both the numerator and denominator to ensure you find the greatest common factor.
-
Dividing only the numerator or denominator: Remember to divide both the numerator and the denominator by the GCF.
-
Not simplifying completely: Always check if the simplified fraction can be further reduced.
Frequently Asked Questions (FAQ)
Q: What if the numerator is 1? Is the fraction already simplified?
A: Yes, if the numerator is 1, the fraction is already in its simplest form. For example, 1/5 cannot be simplified further.
Q: What if the GCF is 1?
A: If the GCF of the numerator and denominator is 1, it means the fraction is already in its simplest form. There are no common factors to divide by.
Q: Can I simplify a fraction by multiplying the numerator and denominator by the same number?
A: No, multiplying both the numerator and denominator by the same number creates an equivalent fraction, but it doesn't simplify it. Simplification involves dividing by a common factor.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand and work with. It's essential for further mathematical operations and for expressing results in a clear and concise manner. Moreover, it helps build a strong foundation for more advanced mathematical concepts.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics. By understanding the concept of the greatest common factor (GCF) and mastering the techniques for finding it (listing factors, prime factorization, Euclidean algorithm), you can confidently simplify any fraction. Remember to always divide both the numerator and denominator by the GCF and to check if the resulting fraction can be further simplified. Practice is key to mastering this essential skill. Start with simple fractions and gradually work towards more complex ones. With consistent effort, you'll build a strong understanding of fractions and their simplification, paving the way for success in more advanced mathematical concepts. The seemingly simple fraction 10/15, through its simplification, illuminates the power of fundamental mathematical principles.
Latest Posts
Latest Posts
-
Ratio Worksheets Grade 6 Pdf
Sep 17, 2025
-
Factors Of 36 In Pairs
Sep 17, 2025
-
15 Percent Of 20 Dollars
Sep 17, 2025
-
500 Yards How Many Miles
Sep 17, 2025
-
7 To The Power Of
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 10 15 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.