15 Percent Of 20 Dollars
keralas
Sep 17, 2025 · 5 min read
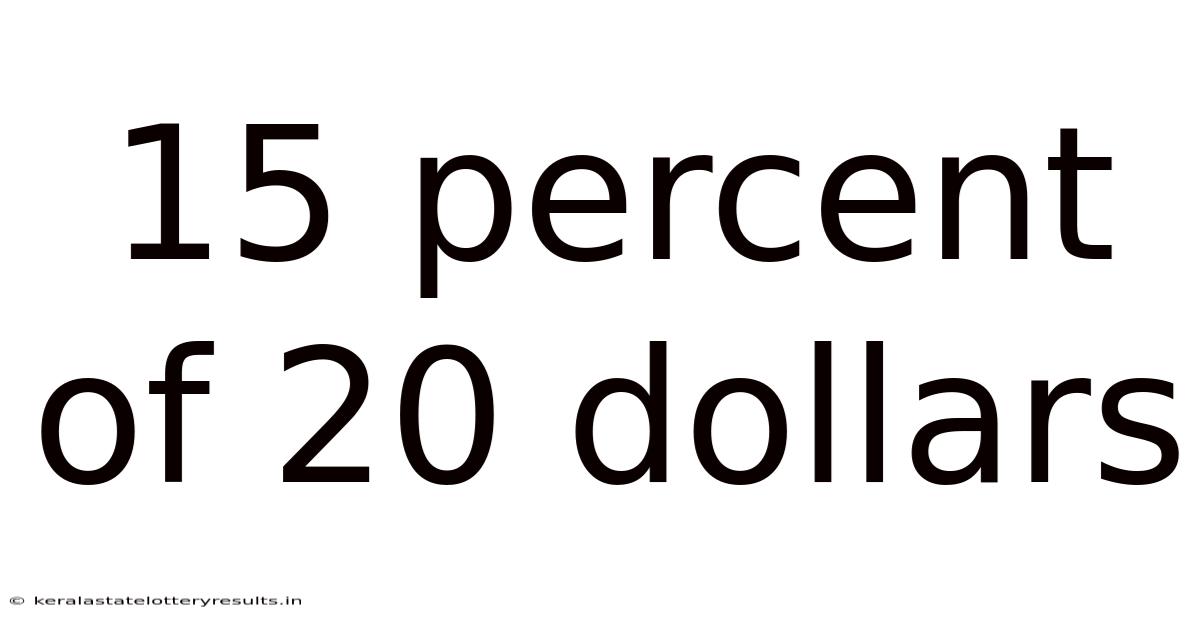
Table of Contents
Decoding 15% of $20: A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous areas of life, from splitting restaurant bills to understanding financial reports. This article will delve into the seemingly simple calculation of 15% of $20, exploring various methods, underlying mathematical principles, and practical applications of percentage calculations. We'll move beyond simply finding the answer and explore the "why" behind the process, equipping you with a deeper understanding of percentages and their widespread use.
Introduction: Understanding Percentages
A percentage represents a fraction of 100. The term "percent" literally means "per hundred" or "out of one hundred." Therefore, 15% signifies 15 out of 100, or 15/100 as a fraction, or 0.15 as a decimal. Understanding this fundamental relationship is key to mastering percentage calculations. We'll utilize this knowledge to easily determine 15% of $20 and explore several approaches to solving this problem.
Method 1: The Decimal Approach
The most straightforward method involves converting the percentage into its decimal equivalent. Since 15% is equal to 0.15, we simply multiply this decimal by the total amount:
0.15 * $20 = $3
Therefore, 15% of $20 is $3. This method is efficient and readily applicable using a calculator or even mental math with practice.
Method 2: The Fraction Approach
Alternatively, we can express 15% as a fraction: 15/100. Then we multiply this fraction by $20:
(15/100) * $20 = $3
This method reinforces the fractional nature of percentages and provides an alternative approach for those who prefer working with fractions. Simplifying the fraction before calculation can also make the process easier; 15/100 simplifies to 3/20, resulting in (3/20) * $20 = $3.
Method 3: The Proportion Approach
The proportion method provides a more visual and intuitive approach, especially when dealing with more complex percentage problems. We can set up a proportion:
15/100 = x/$20
Where 'x' represents the unknown value (15% of $20). To solve for 'x', we cross-multiply:
100x = 15 * $20 100x = $300 x = $300/100 x = $3
This method highlights the relationship between the percentage, the total amount, and the resulting part. It's a valuable technique for understanding the underlying mathematical principles of percentages.
Beyond the Calculation: Real-World Applications
The seemingly simple calculation of 15% of $20 has widespread practical applications. Consider these examples:
- Sales Tax: Many regions impose a sales tax on purchases. If a $20 item has a 15% sales tax, the tax amount would be $3, bringing the total cost to $23.
- Discounts: Stores frequently offer discounts as a percentage. A 15% discount on a $20 item would reduce the price by $3, resulting in a final price of $17.
- Tips: In many cultures, tipping is customary. A 15% tip on a $20 meal would be $3.
- Commission: Salespeople often earn a commission based on a percentage of their sales. If a salesperson earns a 15% commission on a $20 sale, they would earn $3.
- Interest: Interest on loans or investments is often calculated as a percentage of the principal amount. Understanding percentage calculations is crucial for comprehending interest accrual.
- Data Analysis: In data analysis and statistics, percentages are used extensively to represent proportions and trends within datasets. Understanding percentages is essential for interpreting data accurately.
Expanding Your Understanding: Working with Different Percentages
While we've focused on 15% of $20, the principles discussed apply to any percentage and any amount. To calculate any percentage of a given amount, simply convert the percentage to a decimal and multiply it by the amount. For example:
- 25% of $50: 0.25 * $50 = $12.50
- 10% of $100: 0.10 * $100 = $10
- 5% of $30: 0.05 * $30 = $1.50
Practice is key to mastering these calculations. Try calculating various percentages of different amounts to build your proficiency.
Advanced Percentage Calculations: Percentage Increase and Decrease
Percentage calculations extend beyond finding a portion of a total amount. They're also crucial for understanding percentage increases and decreases. For example, if a $20 item increases in price by 15%, the new price would be:
$20 + ($20 * 0.15) = $23
Conversely, if the $20 item decreases in price by 15%, the new price would be:
$20 - ($20 * 0.15) = $17
Understanding percentage increase and decrease is essential for analyzing changes in prices, profits, populations, and numerous other variables.
The Importance of Accuracy in Percentage Calculations
Accuracy in percentage calculations is vital in various contexts. In financial transactions, even small errors can have significant consequences. Always double-check your calculations, especially when dealing with substantial amounts of money. Using a calculator can help minimize errors, but understanding the underlying mathematical principles remains crucial.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate percentages without a calculator?
- A: For simpler percentages like 10%, 25%, or 50%, you can perform mental calculations using fraction equivalents. For other percentages, breaking them down into smaller, easier-to-calculate components can be helpful. For example, 15% can be thought of as 10% + 5%.
-
Q: What if I need to calculate a percentage of a number that is not a whole number?
- A: The process remains the same. Convert the percentage to a decimal and multiply it by the number, regardless of whether the number is a whole number or a decimal.
-
Q: How can I improve my speed and accuracy in calculating percentages?
- A: Practice is key. Regularly work through percentage problems of varying complexity to build your skills and confidence. Familiarize yourself with common percentage equivalents in fraction and decimal form.
-
Q: Are there any online tools or resources to help with percentage calculations?
- A: Yes, numerous online calculators and educational websites provide tools and resources for practicing percentage calculations. These resources can offer immediate feedback and help you learn at your own pace.
Conclusion: Mastering the Power of Percentages
Calculating 15% of $20, while seemingly simple, reveals the fundamental principles underlying percentage calculations. These principles are widely applicable across various disciplines, emphasizing the importance of understanding percentages in both academic and professional settings. By mastering these techniques and practicing regularly, you'll equip yourself with a valuable skill that will significantly benefit you in numerous aspects of life. Remember to approach percentage problems methodically, whether using the decimal, fraction, or proportion method, and always double-check your calculations to ensure accuracy. The ability to confidently and accurately perform percentage calculations is a cornerstone of numerical literacy and empowers you to better understand and navigate the quantitative world around you.
Latest Posts
Latest Posts
-
What Times What Equals 38
Sep 17, 2025
-
72 Inches By 72 Inches
Sep 17, 2025
-
How Many Weeks Ina Month
Sep 17, 2025
-
What Is 93kg In Pounds
Sep 17, 2025
-
70 Km Hr To Mph
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent Of 20 Dollars . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.