X Ln X Dx Integral
keralas
Sep 16, 2025 · 5 min read
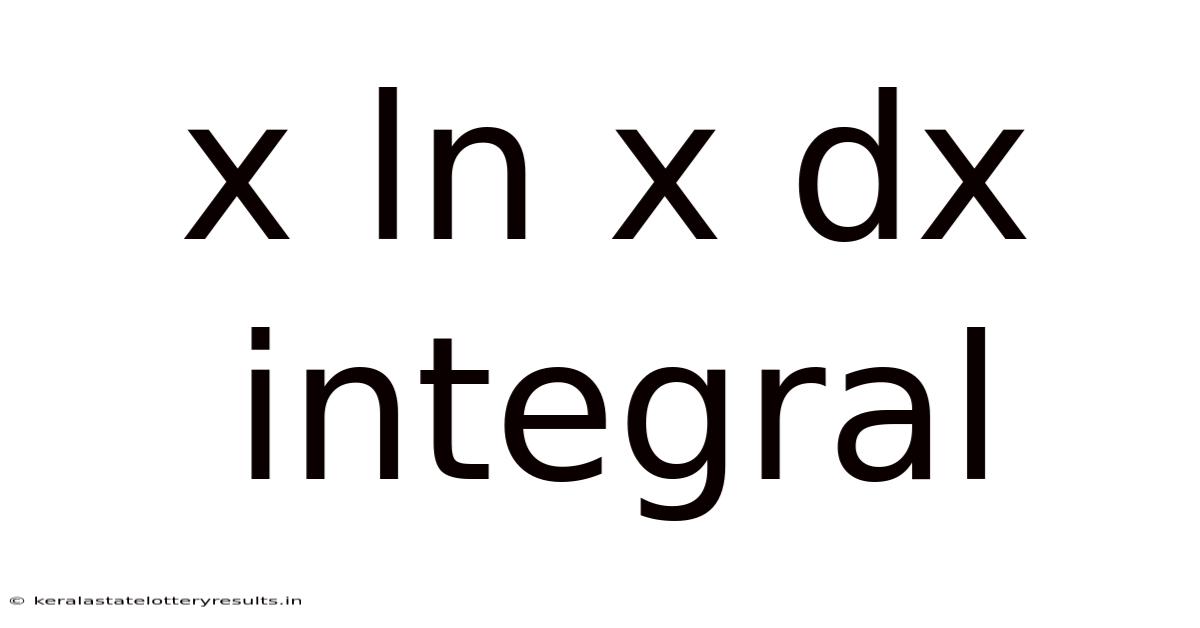
Table of Contents
Decoding the Definite Integral: ∫x ln x dx
The definite integral ∫x ln x dx represents a fascinating challenge in calculus, combining the simplicity of a linear function (x) with the logarithmic function (ln x). Understanding how to solve this integral is crucial for anyone mastering integration techniques and applying them to various scientific and engineering problems. This comprehensive guide will walk you through the solution step-by-step, exploring the underlying mathematical concepts, offering practical examples, and addressing common questions. We will delve into the intricacies of integration by parts, a powerful technique essential to conquer this seemingly complex integral. Mastering this technique will significantly enhance your calculus skillset.
Introduction: Why is ∫x ln x dx Important?
The integral ∫x ln x dx isn't just an abstract mathematical exercise; it has practical applications across numerous fields. It frequently appears in problems related to:
- Probability and Statistics: In calculations involving probability density functions and expected values.
- Physics: Solving differential equations that model physical phenomena, particularly those involving exponential decay or growth.
- Engineering: Analyzing systems with logarithmic relationships between variables, such as signal processing or thermodynamics.
- Economics: In models involving logarithmic utility functions or growth rates.
Therefore, understanding how to solve this integral is not just academically enriching but also practically relevant for students and professionals in various disciplines.
Understanding the Integration by Parts Technique
The key to solving ∫x ln x dx lies in a powerful integration technique called integration by parts. This technique is based on the product rule for differentiation:
d(uv) = u dv + v du
Rearranging this equation and integrating both sides, we get the formula for integration by parts:
∫u dv = uv - ∫v du
Choosing the right 'u' and 'dv' is crucial for effective application of this method. A common mnemonic device is "LIATE," which prioritizes the order of function types for 'u':
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions
- Trigonometric functions
- Exponential functions
This order suggests that logarithmic functions are often the best choice for 'u' when they appear in an integral.
Solving the Integral: A Step-by-Step Approach
Let's apply the integration by parts technique to solve ∫x ln x dx:
-
Choose u and dv: Following the LIATE rule, we choose:
- u = ln x => du = (1/x) dx
- dv = x dx => v = (1/2)x²
-
Apply the integration by parts formula: ∫x ln x dx = uv - ∫v du = (1/2)x²(ln x) - ∫(1/2)x²(1/x) dx
-
Simplify and integrate: ∫x ln x dx = (1/2)x²(ln x) - ∫(1/2)x dx = (1/2)x²(ln x) - (1/4)x² + C
Where 'C' is the constant of integration. Remember to always include the constant of integration when solving indefinite integrals.
Detailed Explanation and Justification
Let's break down the steps further to ensure complete understanding:
-
Step 1: Choosing u and dv: Selecting ln x as 'u' and x dx as 'dv' is strategic. The derivative of ln x, (1/x) dx, is simpler than ln x itself. Integrating x dx yields (1/2)x², a straightforward algebraic function. This choice simplifies the subsequent integration in the formula.
-
Step 2: Applying the formula: The integration by parts formula directly substitutes the chosen 'u', 'du', 'v', and 'dv' values. This is a mechanical process that directly follows the mathematical definition.
-
Step 3: Simplification and Integration: The resulting integral, ∫(1/2)x dx, is a simple power rule integral, easily solved. The constant of integration, 'C', accounts for all possible antiderivatives of the function. The omission of 'C' represents an incomplete solution.
Example: Evaluating a Definite Integral
Let's apply our solution to evaluate a definite integral:
Evaluate ∫₁² x ln x dx
Using our derived solution:
∫x ln x dx = (1/2)x²(ln x) - (1/4)x² + C
We evaluate this between the limits of integration 1 and 2:
[(1/2)(2)²(ln 2) - (1/4)(2)²] - [(1/2)(1)²(ln 1) - (1/4)(1)²] = 2 ln 2 - 1 - (0 - 1/4) = 2 ln 2 - 3/4
Therefore, ∫₁² x ln x dx ≈ 2(0.693) - 0.75 ≈ 0.636
Common Mistakes to Avoid
-
Incorrect application of the integration by parts formula: Double-check that you've correctly substituted 'u', 'du', 'v', and 'dv' into the formula. A single error here will propagate throughout the solution.
-
Forgetting the constant of integration (C): This is a crucial step, especially with indefinite integrals. Omitting 'C' makes the solution incomplete.
-
Improper choice of 'u' and 'dv': While LIATE offers guidance, sometimes experimenting with different choices is necessary. If one choice leads to a more complex integral, reconsider your selection.
-
Algebraic errors: Carefully check your algebraic manipulations throughout the process. A simple mistake can dramatically alter the result.
Frequently Asked Questions (FAQ)
Q1: Can this integral be solved using other techniques?
A1: While integration by parts is the most straightforward approach, other advanced techniques might be applicable, but they would be significantly more complex and less efficient.
Q2: What happens if the limits of integration include zero?
A2: The natural logarithm (ln x) is undefined at x = 0. The integral ∫₀ˣ x ln x dx is an improper integral and requires careful handling using limit techniques.
Q3: How does this integral relate to other logarithmic integrals?
A3: Understanding this integral provides a foundation for tackling more complex logarithmic integrals. Many more intricate integrals can be solved using integration by parts in combination with substitution or other techniques. This integral lays the groundwork for understanding more complex integrations involving logarithmic and algebraic functions.
Q4: Are there online tools or calculators to verify the result?
A4: Many online integral calculators can verify the solution, but it is essential to understand the underlying mathematical process to fully grasp the concepts involved.
Conclusion: Mastering the Art of Integration
Solving ∫x ln x dx isn't merely about getting the right answer; it's about mastering a fundamental technique in calculus – integration by parts. By carefully following the steps, understanding the underlying logic, and practicing with various examples, you'll not only be able to solve this integral but also gain a deeper appreciation for the power and elegance of calculus. Remember, the key is to practice consistently and diligently to build your confidence and skill in tackling increasingly complex integration problems. The ability to confidently solve integrals like this will significantly contribute to your success in advanced mathematics and its applications across various scientific and engineering disciplines. Keep practicing, and you will master this crucial skill.
Latest Posts
Latest Posts
-
Gcf Of 32 And 54
Sep 16, 2025
-
90 Degrees Celsius To Fahrenheit
Sep 16, 2025
-
Gcf Of 42 And 24
Sep 16, 2025
-
Rearrange Expression Into Quadratic Form
Sep 16, 2025
-
Gcf Of 30 And 16
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about X Ln X Dx Integral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.