X 2 5x 6 0
keralas
Sep 14, 2025 · 6 min read
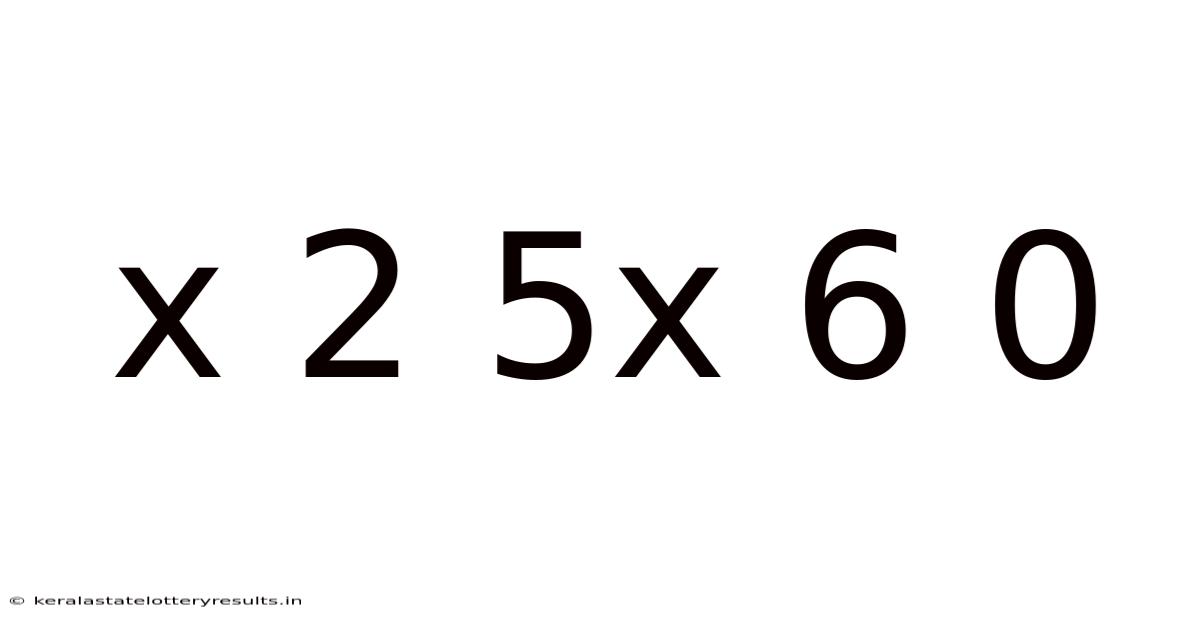
Table of Contents
Decoding the Mystery: x² + 5x + 6 = 0
This article delves into the fascinating world of quadratic equations, specifically addressing the solution of the equation x² + 5x + 6 = 0. We'll explore various methods for solving this seemingly simple equation, providing a comprehensive understanding of the underlying mathematical principles and demonstrating their practical application. Whether you're a high school student grappling with algebra or a curious individual looking to refresh your math skills, this guide will equip you with the tools and knowledge to confidently tackle similar quadratic equations.
Introduction to Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually 'x') is 2. The general form of a quadratic equation is ax² + bx + c = 0, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Our target equation, x² + 5x + 6 = 0, fits this general form with a = 1, b = 5, and c = 6. Understanding quadratic equations is crucial in various fields, from physics and engineering to finance and computer science.
Method 1: Factoring
Factoring is a powerful technique for solving quadratic equations. It involves expressing the quadratic expression as a product of two linear expressions. For our equation, x² + 5x + 6 = 0, we need to find two numbers that add up to 5 (the coefficient of x) and multiply to 6 (the constant term). These numbers are 2 and 3. Therefore, we can factor the equation as follows:
(x + 2)(x + 3) = 0
This equation is satisfied if either (x + 2) = 0 or (x + 3) = 0. Solving these linear equations gives us the solutions:
x = -2 or x = -3
These are the roots or zeros of the quadratic equation. They represent the x-intercepts of the parabola represented by the equation y = x² + 5x + 6.
Method 2: Quadratic Formula
The quadratic formula is a universal method for solving any quadratic equation, regardless of its factorability. It provides a direct way to calculate the roots, even when factoring is difficult or impossible. The formula is derived from completing the square and is given by:
x = [-b ± √(b² - 4ac)] / 2a
For our equation, x² + 5x + 6 = 0, we have a = 1, b = 5, and c = 6. Substituting these values into the quadratic formula, we get:
x = [-5 ± √(5² - 4 * 1 * 6)] / (2 * 1) x = [-5 ± √(25 - 24)] / 2 x = [-5 ± √1] / 2 x = (-5 ± 1) / 2
This gives us two solutions:
x = (-5 + 1) / 2 = -2 x = (-5 - 1) / 2 = -3
As expected, we obtain the same solutions as with the factoring method. The quadratic formula guarantees a solution for all quadratic equations, even those with complex roots (involving imaginary numbers).
Method 3: Completing the Square
Completing the square is another algebraic technique for solving quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored. Let's apply this method to our equation:
x² + 5x + 6 = 0
-
Move the constant term to the right side: x² + 5x = -6
-
Take half of the coefficient of x (which is 5/2), square it (25/4), and add it to both sides: x² + 5x + 25/4 = -6 + 25/4
-
Simplify the right side: x² + 5x + 25/4 = -24/4 + 25/4 = 1/4
-
Factor the left side as a perfect square: (x + 5/2)² = 1/4
-
Take the square root of both sides: x + 5/2 = ±√(1/4) = ±1/2
-
Solve for x: x = -5/2 ± 1/2
This gives us the two solutions:
x = -5/2 + 1/2 = -2 x = -5/2 - 1/2 = -3
Again, we arrive at the same solutions, confirming the accuracy of our methods. Completing the square is a particularly useful technique when dealing with equations that are not easily factorable.
Graphical Representation
The equation x² + 5x + 6 = 0 can be represented graphically as a parabola. The x-intercepts of this parabola correspond to the solutions of the equation. The parabola opens upwards because the coefficient of x² (which is 1) is positive. The vertex of the parabola can be found using the formula x = -b/2a, which in this case is x = -5/2 = -2.5. The y-coordinate of the vertex is obtained by substituting this x-value back into the equation: y = (-2.5)² + 5(-2.5) + 6 = -0.25. Therefore, the vertex of the parabola is at (-2.5, -0.25). The x-intercepts, representing the roots, are at x = -2 and x = -3.
The Discriminant (b² - 4ac)
The discriminant, denoted as Δ (delta), is the expression b² - 4ac within the quadratic formula. It provides valuable information about the nature of the roots:
- Δ > 0: The equation has two distinct real roots (as in our example).
- Δ = 0: The equation has one real root (a repeated root).
- Δ < 0: The equation has two complex conjugate roots (involving imaginary numbers).
In our case, Δ = 5² - 4 * 1 * 6 = 1, which is greater than 0, indicating two distinct real roots.
Applications of Quadratic Equations
Quadratic equations have widespread applications across various disciplines. Some examples include:
- Physics: Calculating projectile motion, determining the trajectory of objects under gravity.
- Engineering: Designing structures, optimizing designs for maximum efficiency.
- Finance: Modeling investment growth, determining break-even points in business.
- Computer Science: Developing algorithms, solving optimization problems.
Frequently Asked Questions (FAQ)
Q: What if I can't factor the quadratic equation easily?
A: Don't worry! The quadratic formula will always work, providing a direct way to find the roots.
Q: What do the solutions of a quadratic equation represent graphically?
A: The solutions represent the x-intercepts (where the parabola intersects the x-axis) of the parabola defined by the equation.
Q: Can a quadratic equation have only one solution?
A: Yes, if the discriminant (b² - 4ac) is equal to zero, the equation has one repeated real root.
Q: What if the discriminant is negative?
A: A negative discriminant indicates that the quadratic equation has two complex conjugate roots, which involve imaginary numbers.
Conclusion
Solving the quadratic equation x² + 5x + 6 = 0 illustrates the power and versatility of various algebraic techniques. Whether you choose factoring, the quadratic formula, or completing the square, the solutions remain consistent: x = -2 and x = -3. Understanding these methods not only solves this specific equation but provides a strong foundation for tackling more complex quadratic equations and appreciating their significance across numerous fields. The graphical representation further enhances understanding by visualizing the relationship between the equation and its solutions. Mastering these techniques unlocks the ability to solve a vast range of mathematical problems and opens doors to deeper exploration in various scientific and technical domains. Remember to choose the method most comfortable and efficient for you, and always check your solutions!
Latest Posts
Latest Posts
-
Whats 70 Degrees In Celsius
Sep 15, 2025
-
Whats 0 4 As A Fraction
Sep 15, 2025
-
Lcm Of 18 And 30
Sep 15, 2025
-
How Tall Is 163 Centimeters
Sep 15, 2025
-
1 3 8 To Inches
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 6 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.